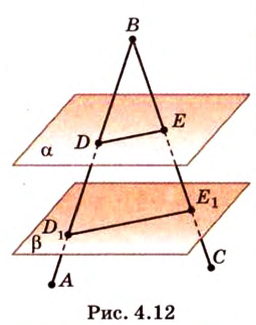
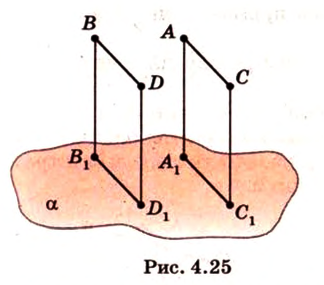
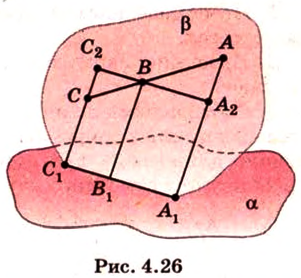
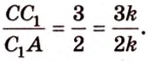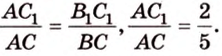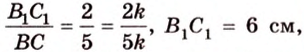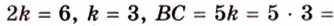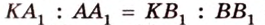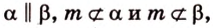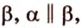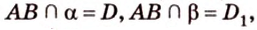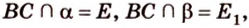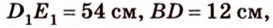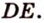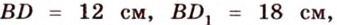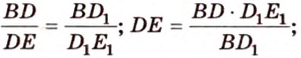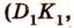Признак скрещивающихся прямых.
Угол между скрещивающимися прямыми
 Взаимное расположение двух прямых в пространстве Взаимное расположение двух прямых в пространстве |
 Признак скрещивающихся прямых Признак скрещивающихся прямых |
 Угол между скрещивающимися прямыми Угол между скрещивающимися прямыми |
- Взаимное расположение двух прямых в пространстве
- Признак скрещивающихся прямых
- Угол между скрещивающимися прямыми
- Взаимное расположение прямых в пространстве, прямой и плоскости с примерами решения
- Взаимное расположение прямых в пространстве
- Взаимное расположение прямой и плоскости в пространстве
- Пример №1
- Параллельность прямой и плоскости
- Пример №2
- Пример №3
- Взаимное расположение двух плоскостей в пространстве. Параллельные плоскости
- Пример №4
- Пример №5
- Свойства параллельных плоскостей
- Пример №6
- Пример №7
- Пример №8
- Параллельное проецирование. Изображение плоских и пространственных фигур на плоскости
- Пример №9
- Точка пересечения прямых в пространстве онлайн
- Предупреждение
- Точка пересечения прямых в пространстве − теория, примеры и решения
- 1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
- 2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
- 3. Точка пересечения прямых в пространстве, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
- 🎬 Видео
Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Взаимное расположение двух прямых в пространстве
Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.
| Фигура | Рисунок | Определение |
| Две пересекающиеся прямые |  | Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку. |
| Две параллельные прямые |  | Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек |
| Две скрещивающиеся прямые | 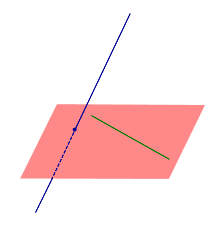 | Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые. |
| Две пересекающиеся прямые |
 |
Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.

Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек

Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.
С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.
| Фигура | Рисунок | Тип утверждения и формулировка |
| Две различные точки |  | Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия. |
| Прямая линия и точка, не лежащая на этой прямой | 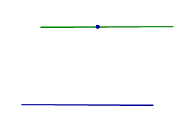 | Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой. |
| Две пересекающиеся прямые | 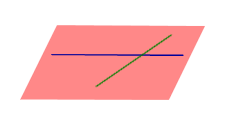 | Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые. |
| Две параллельные прямые | 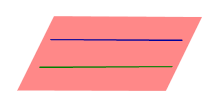 | Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые. |
| Две различные точки |
 |
Аксиома о прямой линии, заданной двумя точками
Через две различные точки проходит одна и только одна прямая линия.

Аксиома о параллельных прямых
Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.

Теорема о плоскости, определяемой двумя пересекающимися прямыми
Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Теорема о плоскости, определяемой двумя параллельными прямыми
Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.
Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Признак скрещивающихся прямых
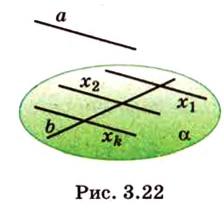
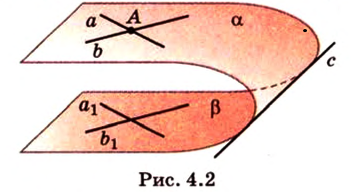
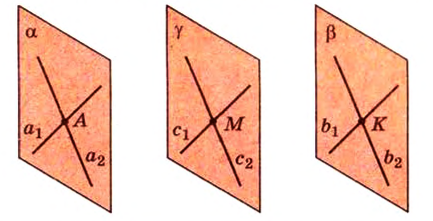
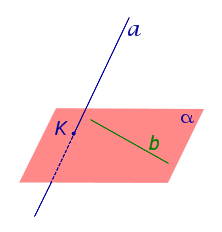
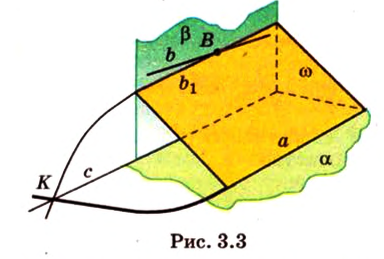
Признак скрещивающихся прямых . Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).
Доказательство . Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».
Для этого предположим, что прямая a , пересекающая плоскость в точке K , и прямая b , лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α . Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K , не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости . Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость , а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Угол между скрещивающимися прямыми
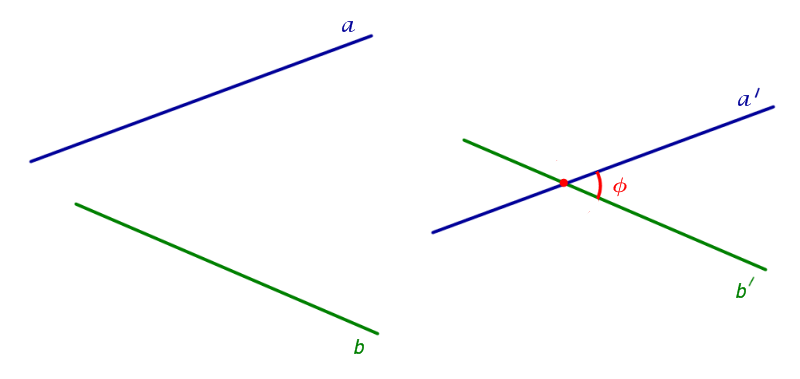
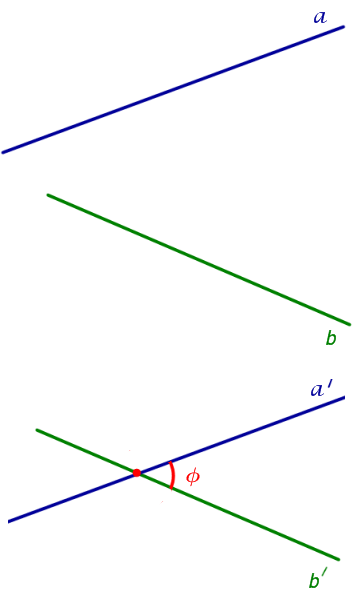
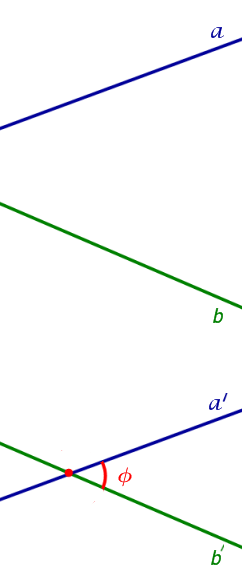
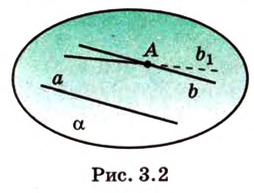
На рисунке 2 изображены скрещивающиеся прямые a и b . Прямая a’ параллельна прямой a , прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b .
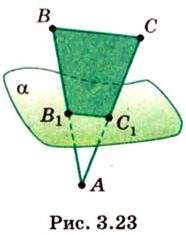
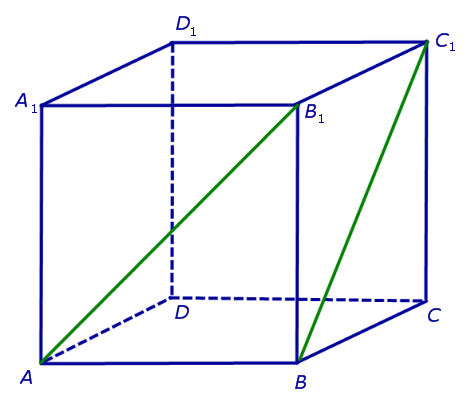
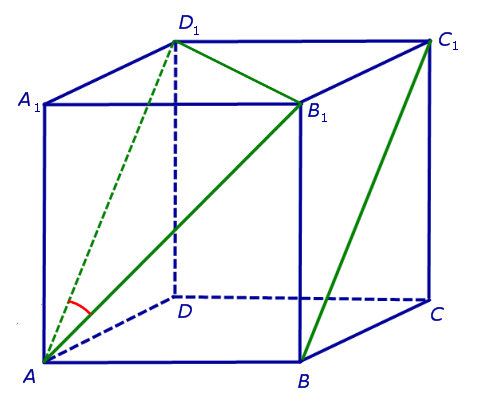
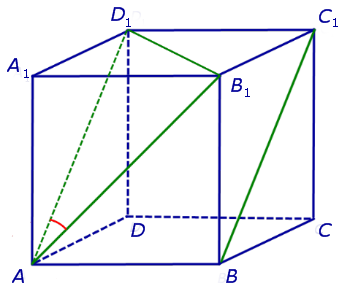
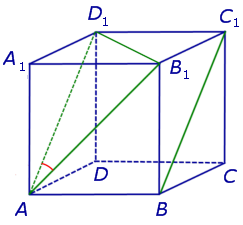
Для того, чтобы найти угол между прямыми AB1 и BC1 , проведем в кубе диагональ боковой грани AD1 и диагональ верхнего основания D1B1 (рис. 4).
Замечание . Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».
Видео:10 класс - Геометрия - Скрещивающиеся прямыеСкачать

Взаимное расположение прямых в пространстве, прямой и плоскости с примерами решения
Содержание:
Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать.
Видео:7. Скрещивающиеся прямыеСкачать

Взаимное расположение прямых в пространстве
Если рассматривать две прямые на плоскости, то они либо не пересекаются, либо пересекаются только в одной точке. Те прямые, которые не пересекаются и лежат в одной плоскости, называют параллельными. А те, которые пересекаются, имеют особое название только в одном случае — если пересекаются под прямым углом. Такие прямые называются перпендикулярными.
Существуют ли в пространстве прямые, которые пересекаются и которые не пересекаются? Ответ на этот вопрос дают образы окружающего мира. Имеют ли такие прямые свое название и как их различать — вы узнаете из этого параграфа.
По аксиоме стереометрии, если две прямые пересекаются, то через них можно провести единственную плоскость. Это означает, что любые две пересекающиеся прямые определяют плоскость, а плоскости, в свою очередь, — пространство.
Итак, в пространстве прямые, расположенные в одной плоскости, могут пересекаться или быть параллельными. По аксиоме параллельных прямых, через точку вне прямой можно провести единственную прямую, параллельную данной. По следствию из аксиомы стереометрии, через прямую и точку вне ее можно провести единственную плоскость. Поэтому выходит, что две параллельные прямые задают плоскость.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Если две произвольные прямые
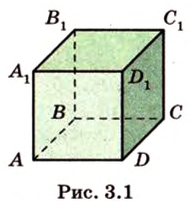
Рассмотрим модель куба, изготовленного из «проволочных отрезков», лежащих на соответствующих прямых (рис. 3.1). Среди прямых, на которых лежат ребра куба, есть такие, которые не пересекаются и лежат в одной плоскости ( 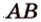
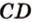
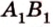
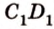
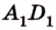
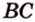
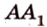
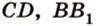
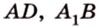
Две прямые пространства, которые не пересекаются и не параллельны, называются скрещивающимися.
Понятно, что две скрещивающиеся прямые не могут лежать в одной плоскости. Поэтому говорят, что две прямые скрещиваются, если их нельзя поместить в одну плоскость. Для определения скрещивающихся прямых используют символ 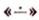

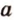
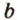
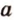
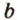
Итак, расположение двух прямых в пространстве может быть следующим:
- прямые пересекаются, если они имеют только одну общую точку;
- прямые параллельны, если они не пересекаются и лежат в одной плоскости;
- прямые скрещиваются, если они не пересекаются и не параллельны;
- прямые совпадают, если они имеют хотя бы две общие точки.
Рассмотрим свойства, которыми обладают параллельные прямые в пространстве.
Теорема 1
Через любую точку пространства, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
Пусть 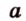
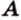
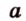
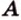
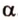
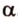

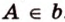
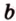
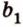
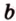
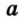

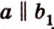
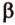
Итак, 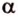
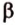
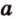
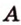
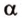
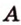
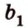
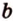
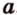
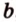
Теорема 2 (признак параллельности прямых)
Если две прямые параллельны третьей прямой, то они параллельны между собой.
Пусть прямые 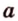
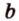
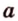
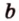
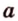
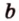
По условию 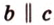
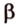
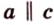
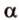
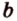
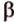
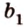

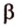
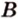
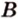
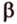
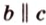
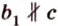
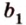
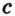
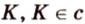

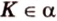
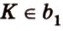
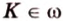
Т.е. точка 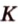
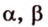
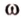
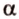
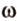
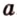
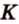
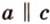
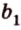
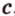
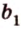
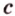
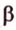
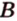
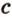
Поэтому прямые 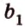
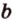
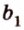
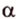
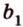
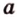
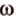
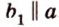
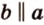
Свойство скрещивающихся прямых выражает признак: если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (предлагаем доказать это самостоятельно).
Взаимное расположение прямой и плоскости в пространстве
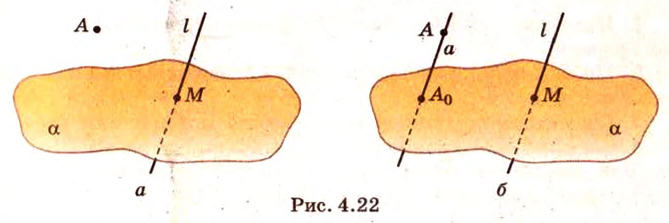
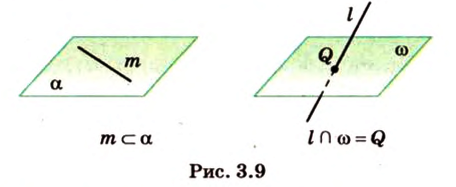
Прямая является подмножеством точек плоскости. Она состоит из множества точек. Такие рассуждения приводят к тому, что прямая и плоскость могут иметь множество общих точек, одну или ни одной общей точки. Случаи, когда прямая принадлежит плоскости и когда прямая пересекает плоскость, нам известны (рис. 3.9). Другие случаи расположения прямой и плоскости рассмотрим в следующих параграфах.
Теорема 3
Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая также пересекает эту плоскость.
Пусть даны параллельные прямые 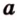
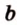
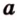
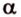
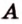
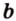
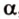
Обозначим 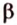
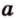
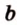
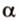
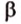
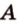

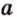
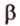
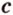
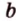
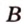
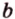
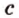
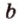
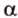
Допустим, что прямая 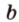
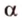
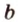
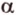
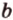
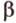
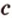
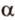
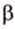
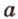
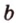
Пример №1
Отрезок 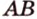
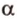
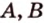
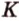
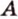
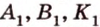
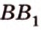
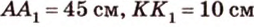
Поскольку прямые 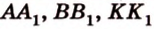
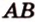

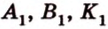
Проведем в плоскости 
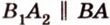
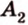
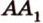
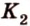
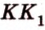
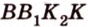
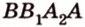
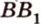
Тогда 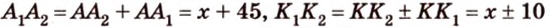
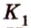
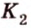
Из подобия треугольников 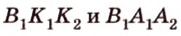
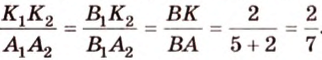
Итак, 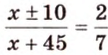
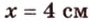
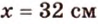
Ответ. 4 см или 32 см.
Отметим, что прямая пересекает плоскость, когда у нее с плоскостью одна общая точка.
Параллельность прямой и плоскости
Рассмотренные в параграфах 3.1 и 3.2 случаи не исчерпывают всех возможных вариантов расположения прямой относительно плоскости. Рассмотрим случай, когда у прямой с плоскостью нет ни одной общей точки. В таком случае говорят, что прямая параллельна плоскости.
Прямая называется параллельной плоскости, если не имеет с ней ни одной общей точки.
Параллельность прямой и плоскости обозначают символом 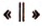
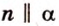
Теорема 4 (признак параллельности прямой и плоскости)
Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Пусть 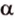
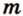
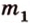
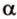
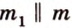
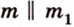
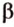
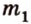
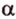
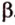
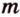
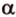
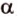
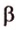
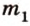
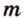
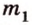
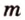
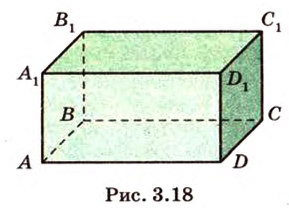
Отрезок называется параллельным плоскости, если он принадлежит прямой, которая параллельна плоскости. Например, и помещении, имеющем форму прямоугольного параллелепипеда, стыки стен с потолком параллельны полу, и наоборот -стыки стен с полом параллельны потолку и т.д. Аналогично можно рассматривать такое расположение на модели прямоугольного параллелепипеда (рис. 3.18):
Следствие 1. Если прямая параллельна плоскости, то через каждую точку этой плоскости на ней можно провести пря мую, параллельную данной прямой.
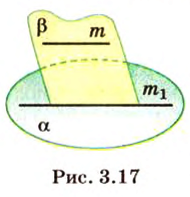
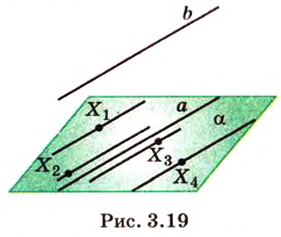
Например, на плоскости 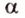
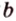
Следствие 2. Существует множество прямых, параллель пых одной и той же плоскости.
Например, вне плоскости 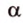
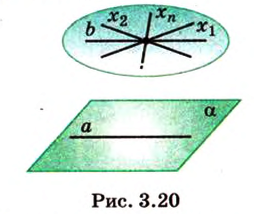
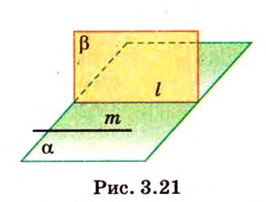
Следствие 3. Если прямая параллельна каждой из пересекаю щихся плоскостей, то она параллельна и прямой их пересечения.
Например, на рисунке 3.21 изображены 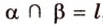
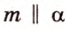
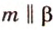
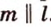
Итак, через точку 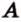
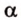
- — множество прямых, параллельных плоскости
,
- — одну прямую
, параллельную прямой
плоскости
,
- — множество прямых, скрещивающихся с прямой
плоскости
Пример №2
Докажите, что все прямые, пересекающие одну из двух скрещивающихся прямых и параллельные другой, лежат в одной плоскости.
Дано: прямые 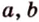
Доказать, что все прямые, пересекающие 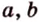
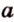
Проведем несколько произвольных прямых 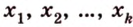
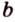
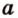
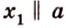
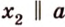
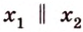
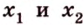
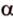
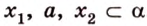
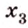
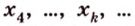
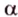
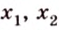
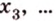
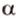
Почему именно так?
Скрещивающиеся прямые 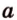

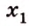
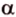
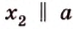

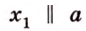
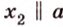
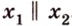

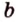
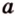
Пример №3
Плоскость 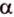
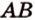
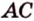
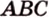
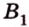
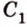
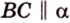
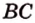
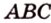
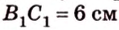
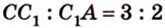
Дано: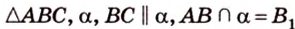
Найти: 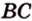
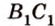
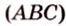
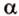
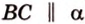
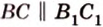
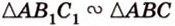
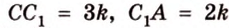
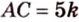
Почему именно так?
Плоскость треугольника 
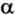
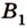
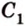
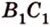
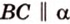
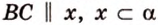
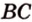
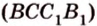
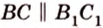
Взаимное расположение двух плоскостей в пространстве. Параллельные плоскости
Если рассматривать две плоскости в пространстве, то их расположение зависит от наличия общих точек.
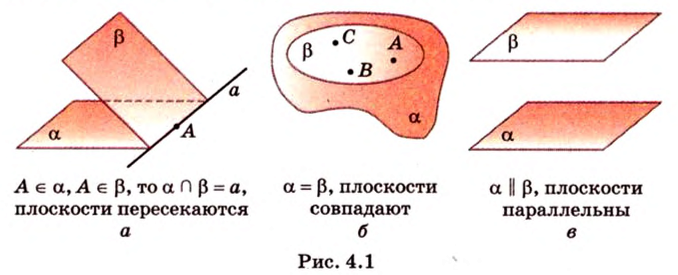
1. Если у двух плоскостей имеется одна общая точка, то они пересекаются по прямой, которая проходит через эту точку (аксиома расположения) (рис. 4.1, а). При наличии двух общих точек ситуация не изменится: через произвольные две точки можно провести только одну прямую, которая будет общей для этих двух плоскостей, т.е. они пересекаются по этой прямой.
Итак, если две плоскости имеют одну или много общих точек, лежащих на одной прямой, то эти плоскости пересекаются.
2. Как известно, через три произвольные точки пространства, не лежащие на одной прямой, можно провести плоскость, и притом только одну (следствие из аксиом стереометрии). Тогда очевидно, что если две плоскости будут иметь три и больше общих точек, не лежащих на одной прямой, то они будут накладываться (рис. 4.1, б). В таком случае говорят, что плоскости совпадают.
Отсюда вытекает, что плоскости совпадают, если они имеют:
- а) общую прямую и точку, не принадлежащую ей;
- б) две общие прямые, которые пересекаются;
- в) хотя бы три общие точки, не лежащие на одной прямой.
3. Если две различные плоскости не имеют ни одной общей точки, то они называются параллельными (рис. 4.1, в). Для обозначения параллельности плоскостей используют символ 
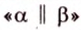
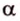
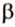
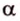
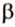
Итак, плоскости в пространстве могут: пересекаться, совпадать или быть параллельными.
Модели параллельных плоскостей встречаются довольно часто: полки в шкафу, двойные стекла в оконной раме, пол и потолок, перекрытия в многоэтажном доме, ровно сложенные в упаковках диски, учебники и т.д. Выяснить, параллельны ли плоскости, позволяет признак параллельности плоскостей.
Теорема 1
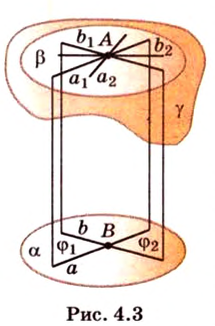
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Пусть 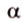
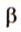
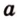
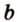
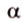
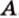
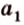
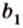
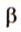
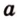
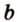
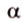
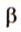
Допустим, что 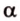
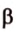

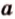
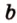
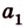
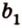
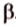
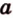
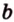
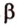
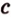
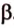
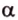
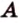
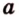
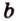

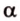
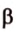
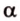
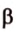
Теорема 2
Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
Пусть 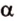
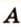
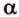
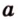
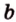
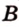
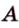
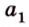
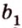
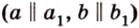
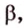
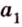
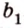
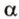
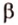
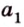
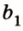
Допустим, что существует другая плоскость 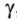
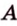
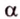
1. Построим плоскость 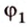
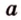
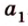
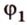
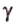
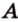
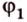
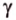
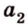
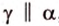
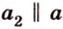
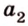
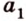
2. Построим плоскость 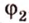
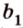
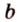
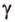
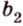
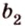
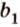
Итак, имеем, что через две пересекающиеся прямые 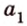
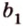
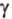
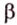
Пример №4
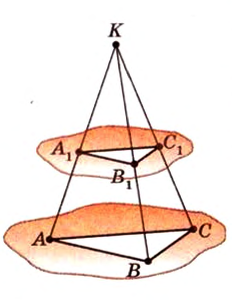
Точка 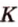
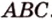
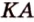
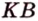
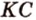
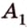
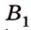
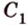

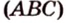
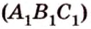
Дано: 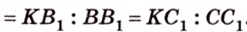
Доказать: 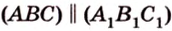
По условию задачи: 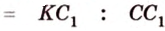
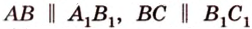
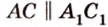
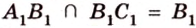
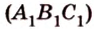
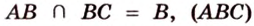
Итак, по признаку параллельности плоскостей, имеем, что 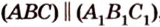
Почему именно так?
По обобщенной теореме Фалеса параллельные прямые отсекают на сторонах угла пропорциональные отрезки. Поэтому, учитывая условие задачи, получаем параллельность трех пар соответствующих прямых: 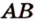
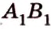
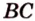
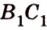
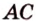
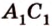
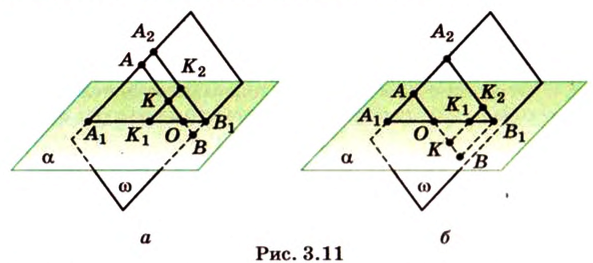
Точками 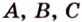
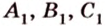
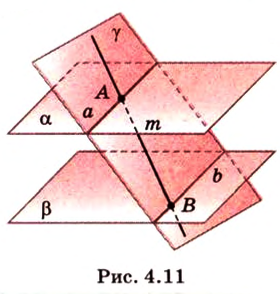
Пример №5
Даны две параллельные плоскости 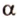
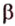
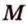
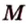
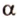
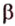
Пусть плоскости 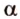
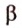
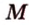
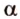
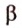
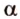
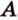
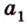
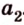
Через точку 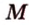
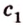
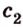
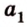
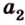
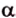
Две пересекающиеся прямые определяют единственную плоскость, пусть это будет плоскость 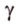
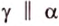
Аналогично доказывается, что 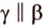
Через точку 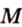
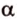
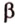
Ответ. Плоскость.
Почему именно так?
Точка 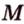
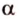
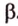
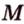
Свойства параллельных плоскостей
Параллельные плоскости имеют определенные свойства. Рассмотрим их.
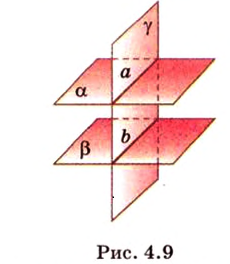
Свойство 1. Если две параллельные плоскости пересечь третьей, то прямые их пересечения параллельны.
Пусть 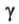
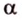
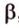
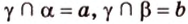
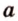
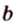
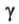
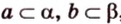
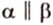
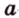
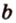
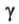
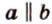
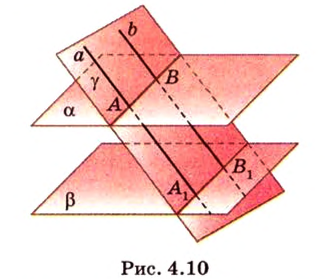
Свойство 2. Параллельные плоскости, пересекая две параллельные прямые, отсекают на них равные отрезки.
Пусть 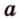
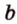
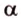
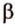
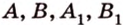
Поскольку прямые 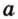
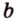
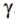
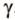
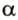
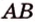
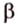
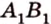
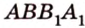
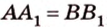
Свойство 2 иногда формулируется так: отрезки параллельных прямых, находящиеся между двумя параллельными плоскостями, равны.
Свойство 3. Две плоскости, параллельные третьей плоскости, параллельны между собой.
Пусть 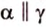
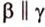
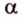
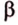
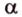
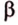
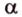
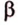
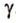
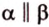
Пример №6
Докажите, что плоскость, пересекающая одну из двух параллельных плоскостей, пересекает и другую плоскость.
Дано: 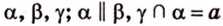
Доказать: плоскость у пересекается с плоскостью 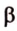
Докажем, что плоскость 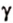
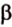
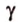
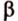
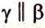
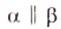
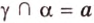

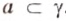
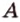
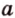
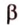
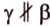
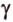
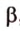
Почему именно так?
Для доказательства требования задачи важно выбрать метод доказательства: прямой или от противного. В общих случаях чаще используют метод от противного. Сделав предположение, противоположное требованию задачи, мы приходим к выводу: 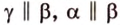
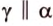
Итак, плоскость, пересекающая одну из двух параллель ных плоскостей, пересекает и другую.
Пример №7
Докажите, что прямая, которая пересекает одну из параллельных плоскостей, пересекает и другую.
Дано: 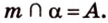
Доказать: прямая 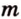
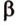
Построим произвольную плоскость 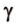
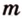
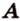
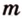
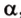
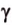
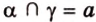
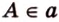
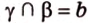
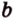
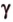
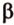
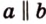
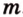
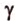
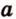
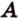
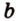
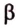
Можно было бы доказать требование задачи методом от противного: предположив, что прямая 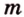
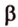
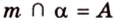
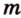
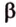

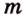
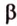
Итак, любая прямая, пересекающая одну из двух параллельных плоскостей, пересекает и другую.
Пример №8
Две параллельные плоскости 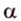
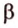
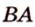
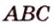
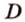
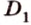
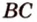
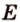
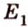
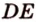
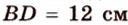
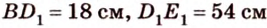
Дано: плоскости 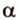
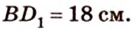
Найти:
Пусть 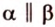
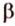
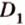
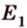
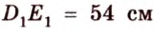
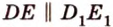
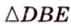
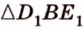
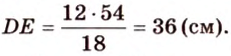
Ответ. 36 см.
Почему именно так?
Через точки 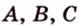
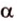
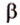
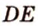
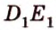
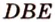
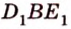
Параллельное проецирование. Изображение плоских и пространственных фигур на плоскости
Чтобы изобразить пространственные фигуры на плоскости, прибегают к разным методам. Один из них — параллельное проецирование.
Параллельное проецирование — это метод изображения произвольной геометрической фигуры на плоскости, при котором все точки фигуры переносятся на плоскость по прямым, параллельным заданной, называющейся направлением проецирования.
Модели параллельного проецирования можно сравнить с тенью на плоской поверхности стены или земли при солнечном освещении. Итак, чтобы выполнить параллельное проецирование, сначала задают фигуру и плоскость, на которую проецируют, — плоскость проекции. Далее задают прямой направление проецирования — проецирующую прямую. Она должна пересекать плоскость проекции.
Пусть заданы произвольная плоскость 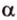
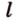
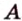
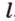
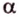
Проведем через точку 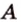
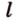
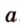
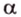
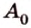
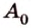
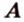
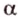
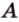
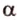
Каждая геометрическая фигура состоит из точек. Поэтому, проецируя последовательно точки фигуры на плоскость, получаем изображение, которое называют проекцией этой фигуры, и способ выполнения изображения — параллельным проецированием.
Отметим, что если точка принадлежит проецирующей прямой, ее проекцией будет точка пересечения прямой с плоскостью (точка 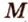
Рассмотрим параллельное проецирование для изображения геометрических фигур на плоскость. Пусть 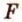
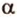
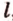
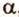
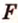
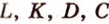
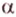
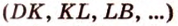
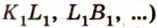
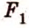
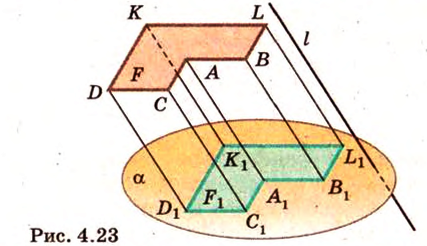
Для параллельного проецирования важно знать его направление. От него зависит общий вид изображения проекции. Например, проекцией отрезка, параллельного проецирующей прямой, будет точка (рис. 4.24, а), а проекцией отрезка, не параллельного проецирующей прямой, — отрезок (рис. 4.24, б).
Итак, параллельное проецирование имеет свои свойства для прямых и отрезков, не параллельных направлению проецирования:
- Проекцией прямой является прямая, а проекцией отрезка — отрезок.
- Проекции параллельных прямых параллельны или совпадают.
- Соотношения длин отрезков одной прямой или параллельных прямых сохраняются (рис. 4.24, б), т.е. равны соотношению длин своих проекций, в частности середина отрезка проецируется в середину его проекции.
Отметим, что длины проекций отрезков, параллельных плоскости проекций, сохраняются, т.е. равны длинам самих отрезков. Отсюда вытекает, что плоская фигура, плоскость которой параллельна плоскости проекции, проецируется в равную себе фигуру.
Приведем некоторые свойства изображения фигуры на плоскости, вытекающие из вышеописанного построения.
Прямолинейные отрезки фигуры изображаются на плоскости рисунка отрезками (рис. 4.24, б).
Действительно, все прямые, которые проецируют точки отрезка 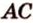
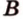
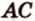
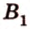
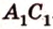
Отметим, что рассмотренные выше отрезки, которые проецируются, не параллельны направлению проецирования.
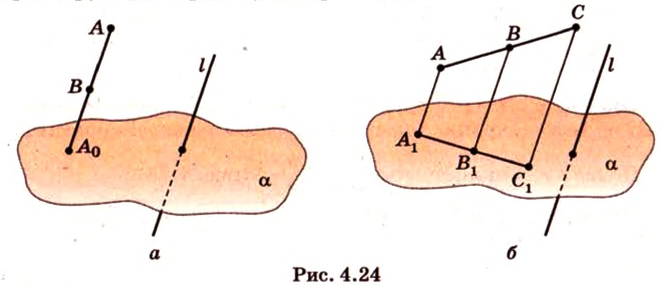
Параллельные отрезки фигуры изображаются на плоскости рисунка параллельными отрезками (рис. 4.25).
Пусть 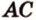
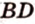
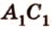
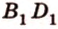
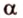
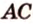
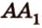
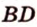
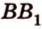
Соотношения длин отрезков одной прямой или параллельных прямых сохраняются при параллельном проецировании.
Покажем, например, что 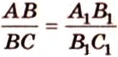
Прямые 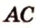
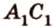
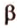
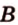
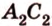
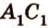

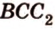
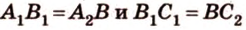
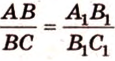
Пример №9
Дана параллельная проекция треугольника. Как построить проекции медиан этого треугольника?
При параллельном проецировании сохраняются соотношения отрезков прямой. Поэтому середина стороны треугольника проецируется в середину проекции этой стороны. Отсюда вытекает, что проекции медиан треугольника будут медианами его проекции.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
- Параллелограмм
- Теорема синусов и теорема косинусов
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Стереометрия для ЕГЭ: 2 - параллельные и скрещивающиеся прямыеСкачать

Точка пересечения прямых в пространстве онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Точка пересечения прямых в пространстве − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в каноническом виде.
- 2. Точка пересечения прямых, заданных в параметрическом виде.
- 3. Точка пересечения прямых, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
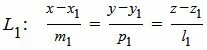 , , | (1) |
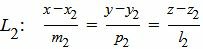 , , | (2) |
Найти точку пересечения прямых L1 и L2 (Рис.1).
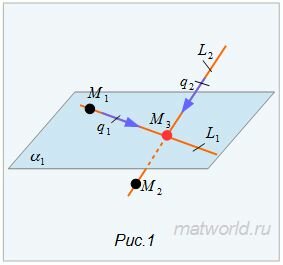 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
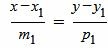 , , | (3) |
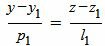 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
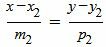 , , | (7) |
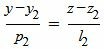 | (8) |
Сделаем перекрестное умножение в уравнениях (7) и (8):
| p2(x−x2)=m2(y−y2) |
| l2(y−y2)=p2(z−z2) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p2x−m2y=p2x2−m2y2, | (9) |
| l2y−p2z=l2y2−p2z2. | (10) |
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
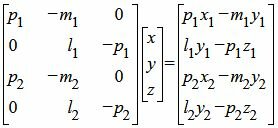 | (11) |
Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L1 и L2 не пересекаются. Если система (11) имеет множество решений, то прямые L1 и L2 совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L1 и L2 .
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
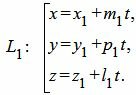 | (12) |
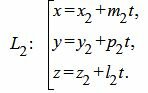 | (13) |
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
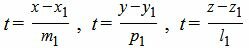 | (14) |
Так как левые части уравнений (14) равны, то можем записать:
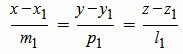 | (15) |
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
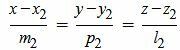 | (16) |
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
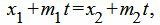 | (17) |
 | (18) |
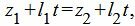 | (19) |
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
 | (20) |
 | (21) |
Представим уравнение (20) в виде двух уравнений:
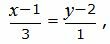 | (22) |
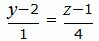 | (23) |
Сделаем перекрестное умножение в уравнениях (22) и (23):
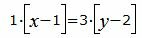 |
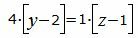 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
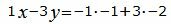 |
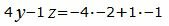 |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
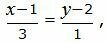 | (26) |
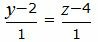 | (27) |
Сделаем перекрестное умножение в уравнениях (7) и (8)
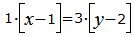 |
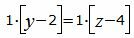 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
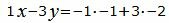 |
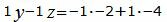 |
Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
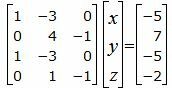 | (30) |
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
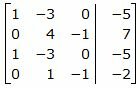 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
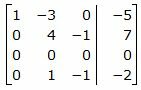 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:
 |
Сделаем перестановку строк 3 и 4.
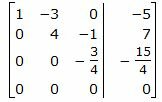 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
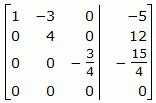 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
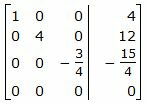 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
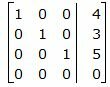 |
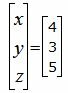 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
 | (31) |
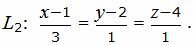 | (32) |
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
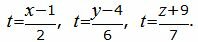 |
Из равентсв выше получим каноническое уравнение прямой:
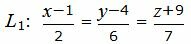 | (33) |
Представим уравнение (33) в виде двух уравнений:
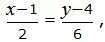 | (34) |
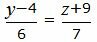 | (35) |
Сделаем перекрестное умножение в уравнениях (34 и (35):
 |
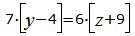 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
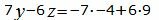 |
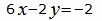 | (36) |
 . . | (37) |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
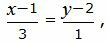 | (38) |
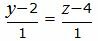 | (39) |
Сделаем перекрестное умножение в уравнениях (38) и (39)
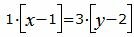 |
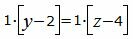 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
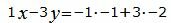 |
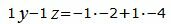 |
Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
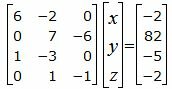 | (42) |
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:
 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
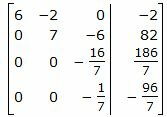 |
Исключим элементы 3-го столбца матрицы ниже элементаa33. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:
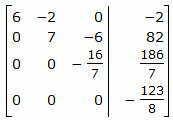 |
Из расширенной матрицы восстановим последнюю систему линейных уравнений:
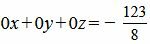 | (43) |
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Прямая L1 имеет направляющий вектор q1=, а прямая L2 имеет направляющий вектор q2=. Эти векторы не коллинеарны. Следовательно прямые L1 и L2 скрещиваются .
🎬 Видео
Параллельность прямых. 10 класс.Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельность прямой и плоскости. 10 класс.Скачать

Скрещивающиеся прямыеСкачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

15. Взаимное расположение прямых в пространствеСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ 10 класс стереометрияСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

✓ Расстояние между скрещивающимися прямыми | ЕГЭ-2018. Задание 13. Математика | Борис ТрушинСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Лекция №4 Чертеж прямой. Следы прямой. Прямые общего и частного положения. Взаимное положение прямыхСкачать

Параллельность прямых. Практическая часть. 10 класс.Скачать


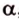 ,
,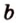 , параллельную прямой
, параллельную прямой  плоскости
плоскости  ,
, плоскости
плоскости