Условие возможности построения треугольника (7 видео)

Существующие треугольники

Содержание

Определение
Теорема
Доказательство теоремы
Определить существование треугольника по трем сторонам
Определить возможность существования треугольника по сторонам
Задача
Решение
🎥 Видео

Определение

Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.

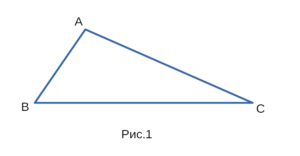
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.

Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.

Теорема

Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.

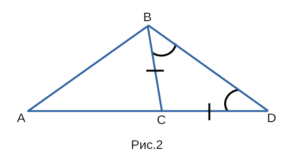
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:

Доказательство теоремы

Проведем отрезок CD равный отрезку CB.
△BCD — равнобедренный, значит ∠ CBD=∠CDB.
Рассмотрим △ABD: ∠ ABD >∠ CBD, следовательно ∠ ABD >∠ CDB, то AB

Видео:Построение треугольника по углу и двум сторонам. 7 класс.Скачать

Определить существование треугольника по трем сторонам

У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится.

Пользователь вводит длины трех сторон. Программа должна определять, может ли существовать треугольник при таких длинах. Это значит, необходимо сравнить суммы всех пар сторон с оставшейся третьей стороной. Чтобы треугольник существовал, сумма всегда должна быть больше отдельной стороны или, по крайней мере, не меньше, если учитывать так называемый вырожденный треугольник.

Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b , b + c , a + c . Первую сумму сравниваем с оставшейся стороной c , вторую — с a и третью — с b . Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.

Можно решить задачу сложнее. Если требуется также определить, какая из сторон больше суммы двух других, то решение может быть таким:

Особого смысла использовать переменную flag здесь нет. Она просто позволяет лишний раз не писать в программе строки, информирующие о том, что треугольник не существует. Большего внимания заслуживает использование вложенных конструкций if-else.

Видео:Построение треугольника по трем сторонам. 7 класс.Скачать

Определить возможность существования треугольника по сторонам

Задача

Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей.

Дано: a , b , c – стороны предполагаемого треугольника.

Требуется сравнить длину каждого отрезка-стороны с суммой двух других. Если хотя бы в одном случае отрезок окажется больше суммы двух других, то треугольника с такими сторонами не существует.

Решение

Ниже приведены решения задачи на языке программирования Паскаль двумя способами. В первом случае все стороны проверяются в одном операторе if; во втором случае каждое условие проверяется отдельно, а программа содержит вложенные операторы if-else.

Программа 1 (предпочтительный способ решения):

В языке Паскаль логический оператор and имеет приоритет над операторам >, if проверяется, что каждая из сторон меньше суммы других. Если хотя бы одна будет больше, то все логическое выражение вернет ложь ( false ). В таком случае сработает ветка else .

В данном случае существование треугольника проверяется по-этапно. Если первое условие возвращает ложь, то программа переходит к последнему else. Если же первое условие соблюдено, то поток выполнения программы оказывается у вложенного if. Здесь проверяется уже второе условие. Если оно возвращает ложь, то программа переходит к предпоследнему else. Если и второе логическое выражение возвращает истину (true), то программа идет к третьему условию. При его соблюдении выполняется тело самого вложенного оператора if. При его несоблюдении сработает самое вложенное else.

Несмотря на то, что данная программа кажется длиннее, в определенных ситуациях она может выполняться быстрее, чем первая. Здесь если внешнее if возвращает ложь, то остальные логические выражения вообще не проверяются. В первой программе могут и проверяться (это зависит от особенностей языка программирования).