В задачах с параметрами Профильного ЕГЭ по математике вам встретятся не только графики функций (в школьном смысле этого слова), но и множества точек на плоскости.
Вот несколько уравнений и неравенств, задающих окружность, круг, ромбик, отрезок. Заметим, что окружность или ромбик, хотя и задаются уравнениями, не являются графиками функций в школьном смысле этого слова. Чтобы лучше почувствовать эту разницу, повторите тему «Что такое функция».
Задачи с параметрами на ЕГЭ по математике считаются одними из самых сложных. Однако на самом деле они похожи на конструктор, где вы собираете решение из готовых элементов. Чтобы уверенно решать задачи с параметрами, необходимо отлично знать 5 типов элементарных функций и их графики. Преобразования графиков функций. И вот эти базовые элементы:
1. Уравнение задает окружность с центром в начале координат и радиусом
2. Уравнение задает окружность с центром в точке (a;b) и радиусом
3. Неравенство задает круг вместе с границей.
4. Уравнение задает верхнюю полуокружность с центром в начале координат и радиусом
5. Уравнение задает нижнюю полуокружность с центром в начале координат и радиусом
6. Уравнение задает верхнюю полуокружность центром в точке и радиусом
7. Уравнение при положительных и задает ромбик, симметричный относительно начала координат.
8. Уравнение (сумма модулей) задает график следующего вида:
9. Расстояние между точками и находится по формуле:
Координаты середины М отрезка АВ находятся по формуле:
Уравнение отрезка концы отрезка и
В левой части уравнения сумма расстояний от точки P с координатами до точек и В правой расстояние между точками и
Пара чисел соответствует координатам любой точки этого отрезка.
Кратко это можно записать так: Это значит, что точка P лежит на отрезке
- Уравнения к полу окружности
- Уравнение окружности и полуокружности. Декартовы координаты точек плоскости
- Примеры решения задач про уравнение окружности
- Задача. Составить уравнение заданной окружности
- Задача. Принадлежит ли точка уравнению окружности
- Построить функцию
- Преимущества построения графиков онлайн
- 📸 Видео
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Уравнения к полу окружности
Найдите все значения а, при каждом из которых система
имеет единственное решение.
Преобразуем первое уравнение системы:
Эти условия задают «верхнюю» полуокружность с центром в точке (−1; −1) радиуса 3. Преобразуем второе уравнение системы:
Эти условия задают «верхнюю» полуокружность с центром в точке (а; а) радиуса 3. Полуокружности, определяемые уравнениями системы, изображены на рисунке 1, обозначим полуокружности через F и Fa, а их центры — О и Оа.
Данная в условии система имеет единственное решение, если полуокружности F и Fa имеют единственную общую точку. Поэтому это необходимо исследовать при различных значения параметра а. Две «верхние» полуокружности одинакового радиуса либо не имеют общих точек, либо имеют ровно одну общую точку, либо совпадают.
При a = −1 полуокружности F и Fa совпадают, т. е. a = −1 не является искомым.
При a > −1, т. е. точка Оа расположена выше точки О. В этом случае полуокружности F и Fa имеют общую точку, если диаметр BC полуокружности Fa имеет общую точку с полуокружностью F. Крайнее положение диаметра BC, при котором он ещё имеет общую точку c полуокружностью F, является положение на рисунке 2, при этом точка Оа имеет координаты (2; 2), т. е. a = 2. При a > 2 полуокружности F и Fa не имеют общих точек. Таким образом, все значения являются искомыми.
При a Ответ:
| Критерии оценивания выполнения задания | Баллы | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Обоснованно получен верный ответ | 4 | |||||||||||||
| Обосновано получен ответ, отличающийся от верного только исключением граничных точек Обосновано получен ответ, отличающийся от верного только включением граничной точки Ответ неверен вследствие одной вычислительной ошибки (описки), не повлиявшей на ход решения и не упростившей задачу | 3 | |||||||||||||
| С помощью верного рассуждения получены промежутки значений a, отличающийся от верного только включением граничной точки и исключением граничных точек С помощью верного рассуждения получен верно только один из промежутков Задача сведена к полному исследованию взаимного расположения двух полуокружностей одной выпуклости и одинакового радиуса и найдено, что при а= -1 они совпадают, а дальнейшие рассуждения выполнены с арифметической ошибкой | 2 | |||||||||||||
| С помощью верного рассуждения получен только один из промежутков, отличающийся от верного только исключением или граничных точек Задача сведена к полному исследованию взаимного расположения двух полуокружностей одной выпуклости и одинакового радиуса и найдено, что при а= -1 они совпадают и начаты дальнейшие рассуждения при аналитическом решении составлено уравнение, например, Видео:Уравнение окружности (1)Скачать  Уравнение окружности и полуокружности. Декартовы координаты точек плоскостиАналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат. В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений. Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию. Геометрическая интерпретация уравнения окружности – это линия окружности. Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности. Окружность с центром в точке А и радиусом R поместим в координатную плоскость. Если координаты центра (а;b) , а координаты любой точки окружности (х; у) , то уравнение окружности имеет вид: Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат. Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:
Видео:Уравнение полуокружностиСкачать  Примеры решения задач про уравнение окружностиЗадача. Составить уравнение заданной окружностиРешение . Подставим значения в формулу. Получаем: Задача. Принадлежит ли точка уравнению окружностиРешение . В уравнение (x — 2) 2 + (y + 3) 2 = 16 Проверим истинность полученного равенства Таким образом, заданная точка не принадлежит заданному уравнению окружности. Если расположить единичную числовую окружность на координатной плоскости, то для ее точек можно найти координаты. Числовую окружность располагают так, чтобы ее центр совпал с точкой начала координат плоскости, т. е. точкой O (0; 0). Обычно на единичной числовой окружности отмечают точки соответствующие от начала отсчета на окружности
На координатной плоскости при указанном выше расположении на ней единичной окружности можно найти координаты, соответствующие этим точкам окружности. Координаты концов четвертей найти очень легко. У точки 0 окружности координата x равна 1, а y равен 0. Можно обозначить так A (0) = A (1; 0). Конец первой четверти будет располагаться на положительной полуоси ординат. Следовательно, B (π/2) = B (0; 1). Конец второй четверти находится на отрицательной полуоси абсцисс: C (π) = C (-1; 0). Конец третьей четверти: D ((2π)/3) = D (0; -1). Но как найти координаты середин четвертей? Для этого строят прямоугольный треугольник. Его гипотенузой является отрезок от центра окружности (или начала координат) к точке середины четверти окружности. Это радиус окружности. Поскольку окружность единичная, то гипотенуза равна 1. Далее проводят перпендикуляр из точки окружности к любой оси. Пусть будет к оси x. Получается прямоугольный треугольник, длины катетов которого — это и есть координаты x и y точки окружности. Четверть окружности составляет 90º. А половина четверти составляет 45º. Поскольку гипотенуза проведена к точке середины четверти, то угол между гипотенузой и катетом, выходящим из начала координат, равен 45º. Но сумма углов любого треугольника равна 180º. Следовательно, на угол между гипотенузой и другим катетом остается также 45º. Получается равнобедренный прямоугольный треугольник. Из теоремы Пифагора получаем уравнение x 2 + y 2 = 1 2 . Поскольку x = y, а 1 2 = 1, то уравнение упрощается до x 2 + x 2 = 1. Решив его, получаем x = √½ = 1/√2 = √2/2. Таким образом, координаты точки M 1 (π/4) = M 1 (√2/2; √2/2). В координатах точек середин других четвертей будут меняться только знаки, а модули значений оставаться такими же, так как прямоугольный треугольник будет только переворачиваться. Получим: При определении координат третьих частей четвертей окружности также строят прямоугольный треугольник. Если брать точку π/6 и проводить перпендикуляр к оси x, то угол между гипотенузой и катетом, лежащим на оси x, составит 30º. Известно, что катет, лежащий против угла в 30º, равен половине гипотенузы. Значит, мы нашли координату y, она равна ½. Зная длины гипотенузы и одного из катетов, по теореме Пифагора находим другой катет: Таким образом T 1 (π/6) = T 1 (√3/2; ½). Для точки второй трети первой четверти (π/3) перпендикуляр на ось лучше провести к оси y. Тогда угол при начале координат также будет 30º. Здесь уже координата x будет равна ½, а y соответственно √3/2: T 2 (π/3) = T 2 (½; √3/2). Для других точек третей четвертей будут меняться знаки и порядок значений координат. Все точки, которые ближе расположены к оси x будут иметь по модулю значение координаты x, равное √3/2. Те точки, которые ближе к оси y, будут иметь по модулю значение y, равное √3/2. Цель урока: ввести уравнение окружности, научить учащихся составлять уравнение окружности по готовому чертежу, строить окружность по заданному уравнению. Оборудование : интерактивная доска.
− (Приложение1 Слайд 2 ) записать формулу нахождения координат середины отрезка; − (Слайд 3) З аписать формулу расстояние между точками (длины отрезка). 3. Объяснение нового материала. (Слайды 4 – 6) Дать определение уравнения окружности. Вывести уравнения окружности с центром в точке (а ;b ) и с центром в начале координат. х 2 + у 2 = R 2 − уравнение окружности с центром в начале координат. Для того чтобы составить уравнение окружности, надо:
4. Решение задач. В задачах № 1 – № 6 составить уравнения окружности по готовым чертежам. № 7. Заполнить таблицу. № 8. Построить в тетради окружности, заданные уравнениями: № 9. Найти координаты центра и длину радиуса, если АВ – диаметр окружности.
№ 10. Составьте уравнение окружности с центром в начале координат, проходящей через точку К (-12;5). R 2 = ОК 2 = (0 + 12) 2 + (0 – 5) 2 = 144 + 25 = 169; Уравнение окружности: х 2 + у 2 = 169. № 11. Составьте уравнение окружности, проходящей через начало координат с центром в точке С (3; — 1). R 2 = ОС 2 = (3 – 0) 2 + (–1–0) 2 = 9 + 1 = 10; № 12. Составьте уравнение окружности с центром А (3;2), проходящей через В (7;5). 1. Центр окружности – А (3;2); № 13. Проверьте, лежат ли точки А (1; -1), В (0;8), С (-3; -1) на окружности, заданной уравнением (х + 3) 2 + (у − 4) 2 = 25. I . Подставим координаты точки А (1; -1) в уравнение окружности: (1 + 3) 2 + (−1 − 4) 2 = 25; II . Подставим координаты точки В (0;8) в уравнение окружности: (0 + 3) 2 + (8 − 4) 2 = 25; III. Подставим координаты точки С (-3; -1) в уравнение окружности: (−3 + 3) 2 + (−1− 4) 2 = 25;
Построить функциюМы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos . Для ввода функций воспользуйтесь левой колонкой. Вводить можно вручную либо с помощью виртуальной клавиатуры внизу окна. Для увеличения окна с графиком можно скрыть как левую колонку, так и виртуальную клавиатуру. Преимущества построения графиков онлайн
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется. 📸 ВидеоПараметр 23 | mathus.ru | единственное решение системы | уравнение полуокружностиСкачать 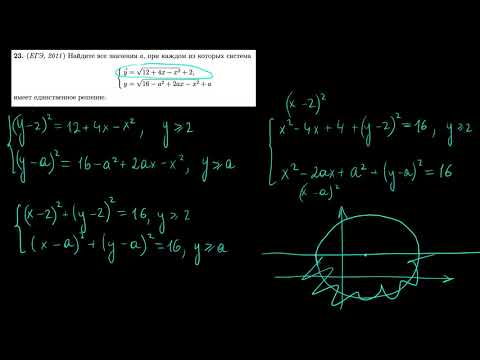 ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать  УРАВНЕНИЕ ОКРУЖНОСТИСкачать  ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать  Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать  начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать  10 класс, 11 урок, Числовая окружностьСкачать  Тригонометрическая окружность. Как выучить?Скачать  Отбор корней по окружностиСкачать  §2 Различные уравнения окружностиСкачать  УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать  Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать  | ||||||||||||||













