Уравнение прямой параллельной оси ох и отсекающей на оси оу отрезок равный 2 имеет вид (8 видео)

Задача 32290 Найти уравнение прямой: а) образующей с.

Содержание

Условие
Решение
Общее уравнение прямой на плоскости. Неполные уравнения прямой
Написать уравнения примой L , где L параллельна оси Ох и отсекает на оси Оу отрезки равные : а)6 б) — 2?
Цилиндр пересечен плоскостью, параллельной оси цилиндра и отстоящей от оси на расстояние 3?
Написать уравнение прямой параллельной оси 0y, проходящей через точку B(3 ; — 1)?
НАЙТИ ОТРЕЗКИ, ОТСЕКАЕМЫЕ НА ОСЯХ КООРДИНАТ ПРЯМЫМИ : у = 2 — 3х?
Написать уравнение прямой проходящей через точку А( — 4 ; 6) и отсекающей осей координат треугольник площадью равной 6?
В цилиндре параллельно оси проведена плоскость, отсекающая от окружности основания дугу в 60°?
Составьте уравнение прямых, проходящих через точку (1 ; 2) и отсекающих на оси абсцисс отрезок, длина которого от начала координат равна 5?
Составить уравнение прямой проходящей через точки ( — 5 ; — 2) и отсекающей оси ординат отрезок в = — 12?
Прямая, проходящая через точку( — 2, 4) отсекает на оси Ох отрезок а = 2?
Помогите пожалуйста)))1)Составить уравнение плоскости, зная, что она отсекает на координатных осях отрезки а = 8, с = — 2 и проходит через точку (1 ; 2 ; 0)?
Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой 2у–х = 3?
💥 Видео

Условие

Найти уравнение прямой:
а) образующей с осью Ox угол pi/3 и пересекающей ось Oу в точке (0;–6)
б) параллельной оси Ох и отсекающей на оси Oу отрезок, равный 2
в) отсекающей на осях координат отрезки, равные 3 и 4.
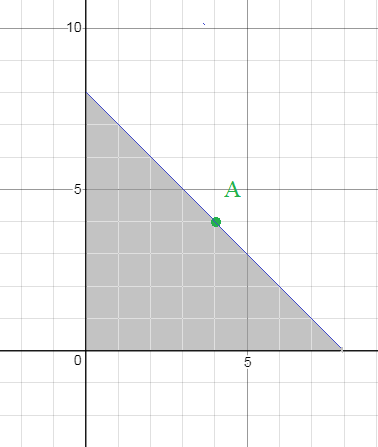
2) Составить уравнение прямой, проходящей через точку А(4;4) и отсекающей от координатного угла треугольник площадью S=4

Решение

а) Уравнение прямой y=kx+b
k_(прямой)=tgα

По условию α =(π/3)

Чтобы найти b подставим координаты точки

-6=sqrt(3)*0+b
b=-6
О т в е т. y=sqrt(3)*x — 6

в)
(x/3)+(y/4)=1
При х=0 получаем y=4 ( отрезок длины 4 на оси Оу)
При у=0 получаем х=3 ( отрезок длины 3 на оси Ох)

a^2-2a+8=0
D

Видео:68. Уравнение прямой в отрезках на осяхСкачать

Общее уравнение прямой на плоскости. Неполные уравнения прямой

Общее уравнение прямой: Ax + By + C = 0. Этим уравнением можно задать любую прямую. Коэффициенты А, В, С при этом определяются не однозначно, а с точностью до пропорциональности.

Уравнение Ax + By + C = 0 называется неполным уравнением прямой на плоскости, если хотя бы один из его коэффициентов А, В, С равен нулю.

Если коэффициент B = 0, A ≠ 0 ≠ C , то из уравнения Ax + By + C = 0 следует x = — C / A = a. Это уравнение прямой, параллельной оси Оу, отсекающей от оси Ох отрезок величиной а.

Если коэффициент A = 0, B ≠ 0 ≠ C то из уравнения Ax + By + C = 0 следует y = — C / B = b. Это уравнение прямой, параллельной оси Ох, отсекающей от оси Оу отрезок величиной b.

Если C = 0, то уравнение Ax + By + C = 0 принимает вид Ax + By = 0. Ясно, что эта прямая проходит через начало координат.

Если в уравнении Ax + By = 0 коэффициент B ≠ 0 , то отсюда получаем y = — x. Обозначив через

k = — , получаем уравнение, которое носит название уравнения прямой с угловым коэффициентом

Если в уравнении Ax + By = 0 A ≠ B = 0, то Ax = 0 и, сокращая на А, получаем уравнение оси Оу: x = 0.

Если в уравнении Ax + By = 0 B ≠ A = 0, то By = 0 и, сокращая на В, получаем уравнение оси Ох: y = 0.

Подведем итог исследования общего уравнения прямой Ax + By + C = 0:

1) Если A ≠ 0, B ≠ 0, C ≠ 0 , то уравнение Ax + By + C = 0 может быть записано в виде уравнения прямой в отрезках: x /a + y / b = 1 – прямая, отсекающая от осей координат отрезки величиной а и b соответственно.

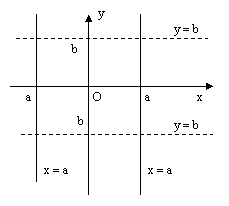
2) Если A = 0, B ≠ 0, C ≠ 0, то уравнение может быть записано в виде: y = b – прямая параллельная оси Ох и отсекающая от оси Оу отрезок величины b.

3) Если A ≠ 0, B = 0, C ≠ 0, то уравнение может быть записано в виде: x = a – прямая параллельная оси Оу и отсекающая от оси Ох отрезок величины а.

4) Если A = 0, B ≠ 0, C = 0, то уравнение прямой имеет вид: y = 0 – прямая совпадает с осью Ох.

5) Если A ≠ 0, B = 0, C = 0, то уравнение прямой имеет вид: x = 0 – прямая совпадает с осью Оу.

6) Если A ≠ 0, B ≠ 0, C = 0, то уравнение может быть записано в виде: y = k * x – уравнение прямой с угловым коэффициентом.

17. Общее уравнение прямой на плоскости. Уравнение прямой в «отрезках» (с выводом)

Уравнение прямой в отрезках: + = 1.Здесь знаменатели а и b – это координаты точек пересечения прямой с соответствующими координатными осями. С помощью такого уравнения невозможно задать прямую, проходящую через начало координат или параллельную одной из осей.

Пусть ни один из коэффициентов А, В, С общего уравнения прямой Ax + By + C = 0, не равен нулю. Перенесем свободный член С в правую часть уравнения и разделим обе части уравнения на (– С):

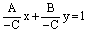
Обозначим . Тогда последнее уравнение можно записать в виде: : + = 1 – это уравнение прямой в отрезках

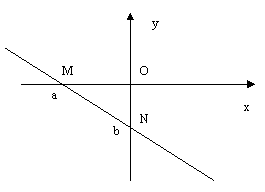
Для построения прямой достаточно взять две точки на этой прямой. Для построения прямой в отрезках удобно найти ее точки пересечения с координатными осями:

М(а, 0) – точка пересечения прямой : + = с осью Ох и

N(0, b) – точка пересечения прямой : + = с осью Оу.

Говорят, что прямая отсекает от координатных осей отрезки ОМ и ОN величина которых равна числам а и b соответственно. Под величиной отрезка ОА здесь понимается не его длина 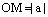, а координата точки М, т.е. число а. Аналогично, величина отрезка ОN равна числу b.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Написать уравнения примой L , где L параллельна оси Ох и отсекает на оси Оу отрезки равные : а)6 б) — 2?

Математика | 10 — 11 классы

Написать уравнения примой L , где L параллельна оси Ох и отсекает на оси Оу отрезки равные : а)6 б) — 2.

Уравнение такой прямой имеет вид : y = b, где b — данные в задаче отрезки.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Цилиндр пересечен плоскостью, параллельной оси цилиндра и отстоящей от оси на расстояние 3?

Цилиндр пересечен плоскостью, параллельной оси цилиндра и отстоящей от оси на расстояние 3.

Секущая плоскость отсекает от окружности основания дугу 60º.

Найдите объем цилиндра, если диагональ сечения равна 4 (считать π = 3).

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Написать уравнение прямой параллельной оси 0y, проходящей через точку B(3 ; — 1)?

Написать уравнение прямой параллельной оси 0y, проходящей через точку B(3 ; — 1).

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

НАЙТИ ОТРЕЗКИ, ОТСЕКАЕМЫЕ НА ОСЯХ КООРДИНАТ ПРЯМЫМИ : у = 2 — 3х?

НАЙТИ ОТРЕЗКИ, ОТСЕКАЕМЫЕ НА ОСЯХ КООРДИНАТ ПРЯМЫМИ : у = 2 — 3х.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Написать уравнение прямой проходящей через точку А( — 4 ; 6) и отсекающей осей координат треугольник площадью равной 6?

Написать уравнение прямой проходящей через точку А( — 4 ; 6) и отсекающей осей координат треугольник площадью равной 6.

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

В цилиндре параллельно оси проведена плоскость, отсекающая от окружности основания дугу в 60°?

В цилиндре параллельно оси проведена плоскость, отсекающая от окружности основания дугу в 60°.

Длина оси 12 см, её расстояние от секущей плоскости 3 см.

Вычислите площадь сечения.

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Составьте уравнение прямых, проходящих через точку (1 ; 2) и отсекающих на оси абсцисс отрезок, длина которого от начала координат равна 5?

Составьте уравнение прямых, проходящих через точку (1 ; 2) и отсекающих на оси абсцисс отрезок, длина которого от начала координат равна 5.

Видео:3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Составить уравнение прямой проходящей через точки ( — 5 ; — 2) и отсекающей оси ординат отрезок в = — 12?

Составить уравнение прямой проходящей через точки ( — 5 ; — 2) и отсекающей оси ординат отрезок в = — 12.

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Прямая, проходящая через точку( — 2, 4) отсекает на оси Ох отрезок а = 2?

Прямая, проходящая через точку( — 2, 4) отсекает на оси Ох отрезок а = 2.

Составьте уравнение этой порямой.

Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Помогите пожалуйста)))1)Составить уравнение плоскости, зная, что она отсекает на координатных осях отрезки а = 8, с = — 2 и проходит через точку (1 ; 2 ; 0)?

1)Составить уравнение плоскости, зная, что она отсекает на координатных осях отрезки а = 8, с = — 2 и проходит через точку (1 ; 2 ; 0).

2)Составить уравнение плоскости, зная, что она отсекает на координатных осях отрезки а = 5, в = 4, с = 2.

3) Записать в виде уравнения в отрезках на осях уравнение прямой 5х — 3у + 10 = 0.

Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой 2у–х = 3?

Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой 2у–х = 3.

Вопрос Написать уравнения примой L , где L параллельна оси Ох и отсекает на оси Оу отрезки равные : а)6 б) — 2?, расположенный на этой странице сайта, относится к категории Математика и соответствует программе для 10 — 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.