Определение треугольника по погорелову

Четырёхугольником называется фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырёхугольника, а соединяющие их отрезки — сторонами четырёхугольника.

Четырёхугольник называется вписанным, если все его вершины лежат на некоторой окружности, и описанным, если все его стороны касаются некоторой окружности.

Вершины четырёхугольника называются соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырёхугольника, называются диагоналями.

Стороны четырёхугольника, исходящие из одной вершины, называются соседними сторонами. Стороны, не имеющие общего конца, называются противолежащими сторонами.

Четырёхугольник обозначается указанием его вершин. Например, ABCD. В обозначении четырёхугольника рядом стоящие вершины должны быть соседними. Четырёхугольник ABCD можно также обозначить BCDA или DCBA. Но нельзя обозначить ABDC (В и D — не соседние вершины).

Сумма длин всех сторон четырёхугольника называется периметром.

Параллелограмм

Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны, т. е. лежат на параллельных прямых.

Теорема 6.1. Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.

Свойство диагоналей параллелограмма

Теорема 6.2 . (обратная теореме 6.1) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Свойство противолежащих сторон и углов параллелограмма

Теорема 6.3 . У параллелограмма противолежащие стороны равны, противолежащие углы равны.

Прямоугольник

Прямоугольник — это параллелограмм, у которого все углы прямые.

Теорема 6.4 . Диагонали прямоугольника равны.

Ромб — это параллелограмм, у которого все стороны равны.

Теорема 6.5. Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов.

Квадрат

Квадрат — это прямоугольник, у которого все стороны равны. Так как стороны квадрата равны, то он является также ромбом. Поэтому квадрат обладает свойствами прямоугольника и ромба.

1. У квадрата все углы прямые.
2. Диагонали квадрата равны.
3. Диагонали квадрата пересекаются под прямым углом и являются биссектрисами его углов.

Теорема Фалеса

Теорема 6.6 . Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Замечание. В условии теоремы Фалеса вместо сторон угла можно взять любые две прямые, при этом заключение теоремы будет то же: параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекают равные отрезки и на другой прямой.

Средняя линия треугольника

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Теорема 6.7 . Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

Трапеция

Трапецией называется четырёхугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.

Теорема 6.8. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Пропорциональные отрезки

Теорема 6.9 . Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

Замечательные точки в треугольнике

Все три биссектрисы треугольника пересекаются в одной точке. Все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке. Все три прямые, содержащие высоты к сторонам треугольника, тоже пересекаются в одной точке (ортоцентр треугольника). Все три медианы треугольника пересекаются в одной точке.

Окружность, описанную около треугольника, вершинами которого являются середины сторон данного треугольника, называют окружностью Эйлера (окружность девяти точек). Середины сторон треугольника и середины отрезков, соединяющих его ортоцентр с вершинами, лежат на одной окружности с центром О, являющейся по определению окружностью Эйлера.

Видео:Неравенства треугольника. 7 класс.Скачать

Раздел 2. Теорема Пифагора

Косинус угла

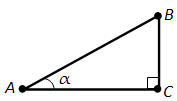
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Косинус угла а обозначается так: cos а и равен отношению катета АС, прилежащего к этому углу, к гипотенузе АВ, т. е. cos a = АС/АВ.

Теорема 7.1. Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.

Это означает, что у двух прямоугольных треугольников с одним и тем же острым углом косинусы этого угла равны.

Теорема Пифагора

Теорема 7.2. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Из теоремы Пифагора следует, что в прямоугольном треугольнике любой из катетов меньше гипотенузы. Отсюда, в свою очередь, следует, что cos а 2 + 4 2 = 5 2 ).

В связи с указанным способом построения прямого угла треугольник со сторонами 3, 4 и 5 единиц иногда называют египетским.

Перпендикуляр и наклонная

Пусть ВА — перпендикуляр, опущенный из точки В на прямую а, и С — любая точка прямой а, отличная от А. Отрезок ВС называется наклонной, проведённой из точки В к прямой а (рис. 153). Точка С называется основанием наклонной. Отрезок АС называется проекцией наклонной.

Из теоремы Пифагора следует, что если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше.

Неравенство треугольника

Если точки А и В различны, то расстоянием между ними называется длина отрезка АВ. Если точки А и В совпадают, то расстояние между ними принимается равным нулю.

Теорема 7.3. Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.

Это значит, что каждое из этих расстояний меньше суммы или равно сумме двух других. Заметим, что в случае, когда точки не лежат на одной прямой, в неравенстве треугольника строгое неравенство. Отсюда следует, что в любом треугольнике каждая сторона меньше суммы двух других сторон.

Соотношения между сторонами и углами в прямоугольном треугольнике

Пусть АВС — прямоугольный треугольник с прямым углом С и острым углом при вершине А, равным а.

• Согласно определению cos а равен отношению катета, прилежащего к углу а, к гипотенузе.
• Синусом угла а (обозначается sin а) называется отношение противолежащего катета ВС к гипотенузе АВ: sin а = ВС/АВ.
• Тангенсом угла а (обозначается tg a) называется отношение противолежащего катета ВС к прилежащему катету АС: tg a = ВС/АС.
• Котангенсом угла а (обозначается ctg a) называется отношение прилежащего катета АС к противолежащему катету ВС: ctga = АС/ВС.

Синус, тангенс и котангенс утла, так же как и косинус, зависят только от величины угла. Из определения sin a, cos a, tg a и ctg a получаем следующие правила:

1. Катет, противолежащий углу а, равен произведению гипотенузы на sin a.
2. Катет, прилежащий к углу а, равен произведению гипотенузы на cos a.
3. Катет, противолежащий углу а, равен произведению второго катета на tg a.
4. Катет, прилежащий к углу а, равен произведению второго катета на ctg a.

Эти правила позволяют, зная одну из сторон прямоугольного треугольника и острый угол, находить две другие стороны; зная две стороны, находить острые углы.

Для sin a, cos a, tg a и ctg a составлены специальные таблицы . Эти таблицы позволяют по данному углу а найти sin a, cos a, tg a и ctg a или по значениям sin a, cos a, tg a и ctg a найти соответствующий угол. В настоящее время для этой цели обычно применяют микрокалькуляторы.

Основные тригонометрические тождества

Эти тождества позволяют, зная одну из величин sin a, cos a, tg a или ctg a, найти три другие.

1. tg a = sin a / cos a.
2. сtg a = cos a / sin a.
3. sin 2 a + cos 2 a = 1.
4. 1 + tg 2 a = 1 / cos 2 a
5. 1 + ctg 2 a = 1 / sin 2 a

Значения синуса, косинуса, тангенса и котангенса некоторых углов

Теорема 7.4. Для любого острого угла a: sin (90° — a) = cos a, cos (90° — a) = sin a.

Изменение синуса, косинуса, тангенса и котангенса при возрастании угла

Теорема 7.5 . При возрастании острого угла sin a и tg a возрастают, а cos a и ctg a убывают.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Раздел 3. Декартовы координаты на плоскости

Определение декартовых координат

Проведём на плоскости через точку О две взаимно перпендикулярные прямые х и у — оси координат. Ось х (она обычно горизонтальная) называется осью абсцисс, а ось у — осью ординат. Точкой пересечения О — началом координат — каждая из осей разбивается на две полуоси. Условимся одну из них называть положительной, отмечая её стрелкой, а другую — отрицательной.

Каждой точке А плоскости мы сопоставим пару чисел — координаты точки — абсциссу (х) и ординату (у) по такому правилу.

Через точку А проведём прямую, параллельную оси ординат. Она пересечёт ось абсцисс х в некоторой точке Ах. Абсциссой точки А мы будем называть число х, абсолютная величина которого равна расстоянию от точки О до точки Ах. Это число будет положительным, если Ах принадлежит положительной полуоси, и отрицательным, если Ах принадлежит отрицательной полуоси. Если точка А лежит на оси у, то полагаем х равным нулю.

Ордината (у) точки А определяется аналогично. Через точку А проведём прямую, параллельную оси абсцисс х. Она пересечёт ось ординат у в некоторой точке Ау. Ординатой точки А мы будем называть число у, абсолютная величина которого равна расстоянию от точки О до точки Ау. Это число будет положительным, если Ау принадлежит положительной полуоси, и отрицательным, если Ау принадлежит отрицательной полуоси. Если точка А лежит на оси абсцисс х, то полагаем у равным нулю. Координаты точки будем записывать в скобках рядом с буквенным обозначением точки, например: А (х; у) (на первом месте абсцисса, на втором — ордината).

Оси координат разбивают плоскость на четыре части — четверти: I, И, III, IV.

Точки оси х (оси абсцисс) имеют равные нулю ординаты (у = 0), а точки оси у (оси ординат) имеют равные нулю абсциссы (х = 0). У начала координат абсцисса и ордината равны нулю.

Плоскость, на которой введены описанным выше способом координаты х и у, будем называть плоскостью ху. Произвольную точку на этой плоскости с координатами х и у будем иногда обозначать просто (х; у). Введённые на плоскости координаты х и у называются декартовыми по имени Р. Декарта, который впервые применил их в своих исследованиях.

Координаты середины отрезка

Пусть А (х1; у1) и В (х2; у2) — две произвольные точки и С (х; у) — середина отрезка АВ. Найдём координаты х, у точки С.
х = (х1 + х2)/2; у = (у1 = у2)/2

Расстояние между точками

Пусть на плоскости ху даны две точки: А1 с координатами х1, у1 и А2 с координатами х2, у2. Выразим расстояние между точками А1 и А2 через координаты этих точек.
d 2 = (х₁ — х₂) 2 + (у₁ — у₂) 2
где d — расстояние между точками А1 и А2.

Уравнение окружности

Уравнением фигуры в декартовых координатах на плоскости называется уравнение с двумя неизвестными х и у, которому удовлетворяют координаты любой точки фигуры. И обратно: любые два числа, удовлетворяющие этому уравнению, являются координатами некоторой точки фигуры.

Составим уравнение окружности с центром в точке А0 (а; b) и радиусом R
(х — а) 2 + (у — b) 2 = R 2 .
Если центром окружности является начало координат, то уравнение окружности имеет вид: х 2 + у 2 = R 2 .

Уравнение прямой

Любая прямая в декартовых координатах х, у имеет уравнение вида ах + by + с = 0, где а, b, с — некоторые числа, причём хотя бы одно из чисел а, b не равно нулю.

Координаты точки пересечения прямых

Координаты точки пересечения являются решением системы уравнений, задающих прямые.

Расположение прямой относительно системы координат

Выясним, как расположена прямая относительно осей координат, если её уравнение ах + by + с = 0 имеет тот или иной частный вид.

1. а = 0, b ≠ 0. В этом случае уравнение прямой можно переписать так: у = -c/b. Таким образом, все точки прямой имеют одну и ту же ординату (-c/b); следовательно, прямая параллельна оси х. В частности, если с = 0, то прямая совпадает с осью х.
2. b = 0, а ≠ 0. Этот случай рассматривается аналогично. Прямая параллельна оси у и совпадает с ней, если и с = 0.
3. с = 0. Прямая проходит через начало координат, так как координаты (0; 0) удовлетворяют уравнению прямой.

Угловой коэффициент в уравнении прямой

Если в общем уравнении прямой ах + by + с = 0 коэффициент при у не равен нулю, то это уравнение можно разрешить относительно у. Получим y = -a/b, x = -c/b. Или, обозначая -a/b = k, -c/b = l, получим у = kx + l.

Коэффициент k в уравнении прямой с точностью до знака равен тангенсу острого угла, который образует прямая с осью х. Коэффициент k в уравнении прямой называется угловым коэффициентом прямой.

График линейной функции

Графиком линейной функции является прямая.

Пересечение прямой с окружностью

Пусть R — радиус окружности и d — расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную к данной,— за ось х (рис. 180). Тогда уравнением окружности будет х 2 + у 2 = R 2 , а уравнением прямой х = d.

Для того чтобы прямая и окружность пересекались, надо, чтобы система двух уравнений х2 + у2 = R2, х = d имела решение. И обратно: всякое решение этой системы даёт координаты х, у точки пересечения прямой с окружностью.

1. Окружность и прямая имеют две точки пересечения, если R > d.
2. Система имеет одно решение, т. е. прямая и окружность касаются, если R = d
3. Система не имеет решения, т. е. прямая и окружность не пересекаются, если R Раздел 4. Движение

Преобразование фигур

Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной.

Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками, т. е. переводит любые две точки X и У одной фигуры в точки X’ и Y’ другой фигуры так, что ХУ = Х’У’.

Замечание. Понятие движения в геометрии связано с обычным представлением о перемещении. Но если мы представляем себе непрерывный процесс, то в геометрии для нас будут иметь значение только начальное и конечное положения фигуры. Два движения, выполненные последовательно, дают снова движение. Преобразование, обратное движению, также является движением.

Свойства движения

Теорема 9.1. Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.

Это значит, что если точки А, В, С, лежащие на прямой, переходят в точки А1, В1, С1, то эти точки также лежат на прямой; если точка В лежит между точками А и С, то точка В1 лежит между точками А1 и С1.

Из теоремы 9.1 следует, что при движении прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки. При движении сохраняются углы между полупрямыми.

Симметрия относительно точки

Пусть О — фиксированная точка и X — произвольная точка плоскости. Отложим на продолжении отрезка ОХ за точку О отрезок ОХ’, равный ОХ. Точка X’ называется симметричной точке X относительно точки О. Точка, симметричная точке О, есть сама точка О. Очевидно, что точка, симметричная точке X’, есть точка X.

Преобразование фигуры F в фигуру F’, при котором каждая её точка X переходит в точку X’, симметричную относительно данной точки О, называется преобразованием симметрии относительно точки О. При этом фигуры F и F’ называются симметричными относительно точки О (рис. 189).

Если преобразование симметрии относительно точки О переводит фигуру F в себя, то она называется центрально-симметричной, а точка О называется центром симметрии.

Например, параллелограмм является центрально-симметричной фигурой. Его центр симметрии — точка пересечения диагоналей.

Теорема 9.2. Преобразование симметрии относительно точки является движением.

Симметрия относительно прямой

Пусть g — фиксированная прямая. Возьмём произвольную точку X и опустим перпендикуляр АХ на прямую g. На продолжении перпендикуляра за точку А отложим отрезок АХ’, равный отрезку АХ. Точка X’ называется симметричной точке относительно прямой g. Если точка X лежит на прямой g, то симметричная ей точка есть сама точка X. Очевидно, что точка, симметричная точке X’, есть точка X.

Преобразование фигуры F в фигуру F’, при котором каждая её точка X переходит в точку X’, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F’ называются симметричными относительно прямой g.

Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры.

Например, прямые, проходящие через точку пересечения диагоналей прямоугольника параллельно его сторонам, являются осями симметрии прямоугольника. Прямые, на которых лежат диагонали ромба, являются его осями симметрии.

Теорема 9.3. Преобразование симметрии относительно прямой является движением.

Поворот

Поворотом плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении.

Это значит, что если при повороте около точки О точка X переходит в точку X’, то лучи ОХ и ОХ’ образуют один и тот же угол, какова бы ни была точка X. Этот угол называется углом поворота. Преобразование фигур при повороте плоскости также называется поворотом.

Параллельный перенос и его свойства

Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (данное определение не является математически строгим).

Параллельный перенос задаётся формулами х = х + а, у’ = у + b. Эти формулы выражают координаты х’, у’ точки, в которую переходит точка (х; у) при параллельном переносе.

Параллельный перенос есть движение. Параллельный перенос сохраняет расстояния, а значит, является движением. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. При параллельном переносе прямая переходит в параллельную прямую (или в себя).

Существование и единственность параллельного переноса. Сонаправленность полупрямых

Теорема 9.4. Каковы бы ни были две точки А и А’, существует один и только один параллельный перенос, при котором точка А переходит в точку А’.

Две полупрямые называются одинаково направленными или сонаправленными, если они совмещаются параллельным переносом, т. е. существует параллельный перенос, который переводит одну полупрямую в другую.

Если полупрямые а и b одинаково направлены и полупрямые b и с одинаково направлены, то полупрямые а и с тоже одинаково направлены.

Две полупрямые называются противоположно направленными, если каждая из них одинаково направлена с полупрямой, дополнительной к другой.

Геометрические преобразования на практике

Известно, что геометрия как наука выросла из практического землемерия. А теперь сама она имеет большое прикладное значение. В частности, на практике широко используются геометрические преобразования

Равенство фигур

Две фигуры называются равными, если они движением переводятся одна в другую. Для обозначения равенства фигур используется обычный знак равенства. Запись F = F’ означает, что фигура F равна фигуре F’. В записи равенства треугольников: DАВС = DA1B1C1 — предполагается, что совмещаемые при движении вершины стоят на соответствующих местах. При таком условии равенство треугольников, определяемое через их совмещение движением, и равенство, как мы его понимали до сих пор, выражают одно и то же.

Это значит, что если у двух треугольников соответствующие стороны равны и соответствующие углы равны, то эти треугольники совмещаются движением. И обратно: если два треугольника совмещаются движением, то у них соответствующие стороны равны и соответствующие углы равны.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Раздел 5. Векторы

Абсолютная величина и направление вектора

Вектор — это направленный отрезок. Направление вектора определяется указанием его начала и конца. На чертеже направление вектора отмечается стрелкой. Для обозначения векторов будем пользоваться строчными латинскими буквами а, b, с, … . Можно также обозначать вектор указанием его начала и конца. При этом начало вектора ставится на первом месте. Вместо слова «вектор» над буквенным обозначением вектора иногда ставится стрелка или черта.

Векторы АВ и CD называются одинаково направленными, если полупрямые АВ и CD одинаково направлены. Векторы АВ и CD называются противоположно направленными, если полупрямые АВ и CD противоположно направлены.

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор.

Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулём с чёрточкой (0). О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю.

Равенство векторов

Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. Из данного определения равенства векторов следует, что

равные векторы одинаково направлены и равны по абсолютной величине. Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.

Координаты вектора

Пусть вектор а имеет началом точку А1 (х1; у1), а концом точку А2 (х2; у2). Координатами вектора а будем называть числа а1 = х2 – х1, а2 = у2 – у1. Координаты нулевого вектора равны нулю.

Равные векторы имеют равные соответствующие координаты. И обратно: если у векторов соответствующие координаты равны, то векторы равны.

Сложение векторов

Суммой векторов а и b с координатами а1, а2 и b1, b2 называется вектор с с координатами a1 +b1, a2 + b2.

Теорема 10.1. Каковы бы ни были точки А, В, С, имеет место векторное равенство АВ + ВС = АС.

Сложение сил

Силу, приложенную к телу, удобно изображать вектором, направление которого совпадает с направлением действия силы, а абсолютная величина пропорциональна величине силы. Как показывает опыт, при таком способе изображения сил равнодействующая двух или нескольких сил, приложенных к телу в одной точке, изображается суммой соответствующих им векторов.

Представление силы в виде суммы сил, действующих в двух заданных направлениях, называется разложением силы по этим направлениям. Удобно производить разложение вектора по двум перпендикулярным осям. В этом случае составляющие вектора называются проекциями вектора на оси.

Умножение вектора на число

Произведением вектора (а1; а2) на число λ называется вектор (λа1; λа2).

Теорема 10.2. Абсолютная величина вектора λа равна |λ| |a|. Направление вектора λа при а ≠ 0 совпадает с направлением вектора а, если λ > 0, и противоположно направлению вектора а, если λ 2 и называется скалярным квадратом.

Для любых векторов а(а1; а2), b(b1; b2), с(с1; с2)
(а + b) • с = ас + bс.

Теорема 10.3. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.

Из теоремы 10.3 следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нулевого векторов равно нулю, то векторы перпендикулярны.

Разложение вектора по координатным осям

Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.

Для любого вектора a (a1; а2) получается разложение а = а1е1 + а2е2.

Вы смотрели «Геометрия 8 Погорелов: все теоремы и определения» — краткое повторение геометрии за 8 класс (основные понятия, определения и теоремы без доказательств ).

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Определение треугольника по погорелову

Вопрос 1. Дайте определение косинуса острого угла прямоугольного треугольника.
Ответ. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинус угла (alpha) обозначается так: (cos alpha). На рисунке 147 показан прямоугольный треугольник ABC с углом A, равным (alpha). Косинус угла (alpha) равен отношению катета AC, прилежащего к этому углу, к гипотенузе AB, т.е.

Вопрос 2. Докажите, что косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.
Ответ. Теорема 7.1. Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.
Это означает, что у двух прямоугольных треугольников с одним и тем же острым углом косинусы этого угла равны.
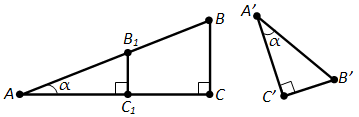
Доказательство. Пусть ABC и A’B’C’ — два прямоугольных треугольника с одним и тем же углом при вершинах A и A’, равным (alpha) (рис. 148). Требуется доказать, что

Построим треугольник AB₁C₁, равный треугольнику A’B’C’, как показано на рисунке 148. Так прямые BC и B₁C₁ перпендикулярны прямой AC, то они параллельны. По теореме о пропорциональных отрезках

А так как по построению AC₁ = A’C’, AB₁ = A’B’, то

Вопрос 3. Докажите теорему Пифагора.
Ответ. Теорема 7.2 (теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
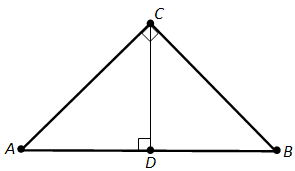
Доказательство.Пусть ABC – данный прямоугольный треугольник с прямым углом C. Проведём высоту CD из вершины прямого угла C (рис. 149).

По определению косинуса угла (cos A = frac = frac). Отсюда (AB cdot AD = AC^2). Аналогично (cos B = frac = frac). Отсюда (AB cdot BD = BC^2). Складывая полученные равенства почленно и замечая, что (AD + DB = AB), получим:

Видео:Признаки равенства треугольников. 7 класс.Скачать

Подготовка к зачету за курс геометрии 7 класса по учебнику Погорелова А.В. Свойства, аксиомы, признаки.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Подготовка к зачету по геометрии за курс 7 класса.

Основные свойства, аксиомы и признаки.

Основные свойства принадлежности точек принадлежности точек и прямых:

Какова бы ни была прямая, существует точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые 2 точки можно провести прямую, и только одну.

Основные свойства расположения точек на прямой

Из трех точек на прямой одна и только одна лежит между двумя другими.

Основные свойства измерения отрезков

Каждый отрезок имеет определенную длину, большую нуля.

Длина отрезка равна сумма длин частей, на которые он разбивается любой его точкой.

Основное свойство расположения точек относительно прямой на плоскости

Прямая разбивает плоскость на две полуплоскости.

Основные свойства измерения углов

Каждый угол имеет определенную градусную меру, большую нуля.

Развернутый угол равен 180 градусов.

Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Основные свойства откладывания отрезков и углов

На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.

От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.

8. Свойство существования треугольника, равного данному

Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

9. Основное свойство параллельных прямых (аксиома параллельных):

Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Глава 2. Смежные и вертикальные углы.

1. Если два угла равны, то смежные с ним углы равны.

2. Если угол не развернутый, то его градусная мера меньше 180°.

Следствие из Т. О смежных углах:

Угол, смежный с прямым углом, есть прямой угол.

Глава 3. Признаки равенства треугольников.

Глава 4. Сумма углов треугольника.

Следствие из теоремы о признаке параллельности прямых:

Две прямые, перпендикулярные третьей параллельны.

Признак параллельности прямых по соответственным углам:

Прямые параллельны, если соответственные углы равны.

Следствие: Через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и только одну.

Следствие из свойства углов, образованных при пересечении параллельных прямых секущей:

Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.

Свойство из теоремы о суммы углов треугольника:

У любого треугольника хотя бы два угла острые.

Св-во из из теоремы о внешних углах треугольника:

Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.

Признаки равенства прямоугольных треугольников:

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны. (Признак равенства по гипотенузе и острому углу)

Если катет и противолежащий ему угол одного прямоугольного треугольника соответственно равны катету и противолежащему углу другого треугольника, такие треугольники равны. (Признак равенства по катету и противолежащему углу).

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны. (Признак равенства по гипотенузе и катету).

Глава5. Геометрические построения

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 988 человек из 78 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 672 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:8 класс, 20 урок, Определение подобных треугольниковСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 540 138 материалов в базе

Материал подходит для УМК

«Геометрия», Погорелов А.В.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 13.03.2018
• 2083
• 14

• 13.03.2018
• 1178
• 7

• 13.03.2018
• 1475
• 20

• 13.03.2018
• 1710
• 9

• 12.03.2018
• 588
• 1

• 12.03.2018
• 1125
• 1

• 12.03.2018
• 601
• 0

• 12.03.2018
• 334
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 13.03.2018 1251
• DOCX 16.6 кбайт
• 17 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Кенжакаева Зоя Тахировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 4 месяца
• Подписчики: 0
• Всего просмотров: 2137
• Всего материалов: 3

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Минобороны начало вакцинацию подростков от COVID-19

Время чтения: 1 минута

В России классы будут переводить на дистант, если заболели 20% детей

Время чтения: 1 минута

Детский омбудсмен призвала предусматривать в школах условия для детей с инвалидностью

Время чтения: 3 минуты

Пермский Роспотребнадзор предписал перевести обучение в школах и ссузах на дистант

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💥 Видео

Первый признак равенства треугольников. 7 класс.Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Треугольники. 7 класс.Скачать

§ 4 № 1-51 - Геометрия 7-9 класс ПогореловСкачать

8 класс, 19 урок, Пропорциональные отрезкиСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать