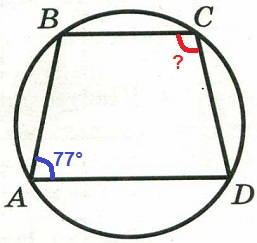
Задание 17. Угол А трапеции ABCD с основаниями AD и ВС, вписанной в окружность, равен 77°. Найдите угол С этой трапеции. Ответ дайте в градусах.
Для любого четырехугольника, вписанного в окружность, соблюдается равенство:
(сумма противоположных углов 180°). Отсюда находим величину угла C:
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Решение №1614 Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 77°.
Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 77°. Найдите угол С этой трапеции. Ответ дайте в градусах.
Источник задания: ОГЭ 2021 Математика, И.В. Ященко. 36 вариантов.
Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º.
Углы ∠А и ∠С противоположные. Найдём угол ∠С:
∠С = 180° – ∠А = 180° – 77° = 103°
Ответ: 103.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Видео:Задача 6 №27636 ЕГЭ по математике. Урок 77Скачать

Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Видео:77. Вписанная окружностьСкачать

Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Видео:Окружность, вписанная в трапециюСкачать

Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Видео:ЕГЭ 2023 математика Вариант 5 задача 1Скачать
Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
📹 Видео
77 задач по геометрии ОГЭ 2023Скачать

Задание 3 (№ 27704) ЕГЭ по математике. Урок 77Скачать
МНЕ ТЯЖЕЛО СВЕТИТЬ! Неправильная Мантикора. Серия 23Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Задание №26 ОГЭ по математикеСкачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Задача про трапецию, описанную около окружностиСкачать

ОГЭ. Понятный разбор задачи №26. Две окружности радиусов 44 и 77 касаются внешним образом...Скачать

Малоизвестные свойства равнобедренной трапеции. Разбор задачи 17 ЕГЭ профиль.Скачать
Найдите углы трапецииСкачать

16 ИЗ ОГЭ // ЕСЛИ ЗНАЕШЬ ЭТО, ТО РЕШИШЬ ЗА 10 сек // Окружность// МатематикаСкачать

Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Вариант 77, № 7. Свойство касательной. Теорема о касательных, проведенных из одной точки. Задача 1Скачать