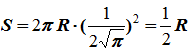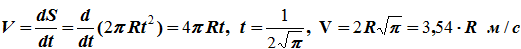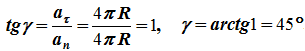Угол между вектором полного ускорения и радиусом окружности

Пример решения задачи по определению в заданный момент времени угла между вектором ускорения точки, движущейся по траектории окружности и радиусом этой окружности.

Видео:Физика - движение по окружностиСкачать

Задача

Точка движется по окружности радиуса R по закону: S=2πRt 2 .

В момент времени:

сек, определить угол между вектором ускорения и радиусом.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Решение

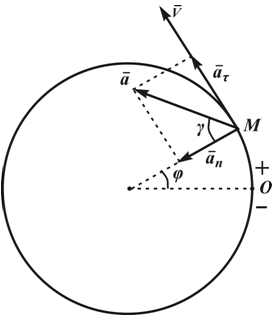
Выбрав начало отсчета и положительное направление движения, показываем положение точки в заданный момент времени:

При длине дуги (1/2)R центральный угол φ=S/R=1/2 рад.

Вектор скорости направлен по касательной к траектории движения, в сторону возрастания дуговой координаты.

Касательное, нормальное и полное ускорения точки:

Угол между вектором ускорения и радиусом :

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:Центростремительное ускорение. 9 класс.Скачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Угол между векторами. 9 класс.Скачать

I. Механика

Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Видео:Ускорение при равномерном движении по окружностиСкачать

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Видео:Вращательное движение. 10 класс.Скачать

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Видео:угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Видео:Иродов. Решение задачи 1.38Скачать

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Найти угол составляемый вектором полного ускорения с радиусом колеса

Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

UptoLike

Колесо радиусом R = 5см вращается так, что зависимость линейной скорости точек, лежащих на ободе колеса, от времени дается уравнением v=At+Bt 2 , где А = 3 см/с 2 и В = 1 см/с 3 . Найти угол α, составляемый вектором полного ускорения с радиусом колеса в моменты времени t, равные: 0, 1, 2, 3, 4 и 5с после начала движения.

Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

ОПРЕДЕЛЕНИЯ

• мера наклона между двумя прямыми линиями или плоскостями, а также величины вращательного движения

величина, имеющая размер и направление.

• расстояние или прямая от центра окружности или сферы к любой точке окружности или поверхности сферы

• движение вокруг своей оси по окружности

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Дополнительные материалы

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Похожие задачи

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Найти через время после начала движения угловую скорость

Колесо радиусом R = 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ=А+B+Ct 2 , где В = 2 рад/с и С = 1 рад/с 3 .

Во сколько раз нормальное ускорение больше ее тангенциального ускорения

Во сколько раз нормальное ускорение а_n точки, лежащей на ободе колеса, больше ее тангенциального ускорения а_τ для того момента, когда вектор полного ускорения точки составляет угол α = 30° с вектором ее линейной скорости?