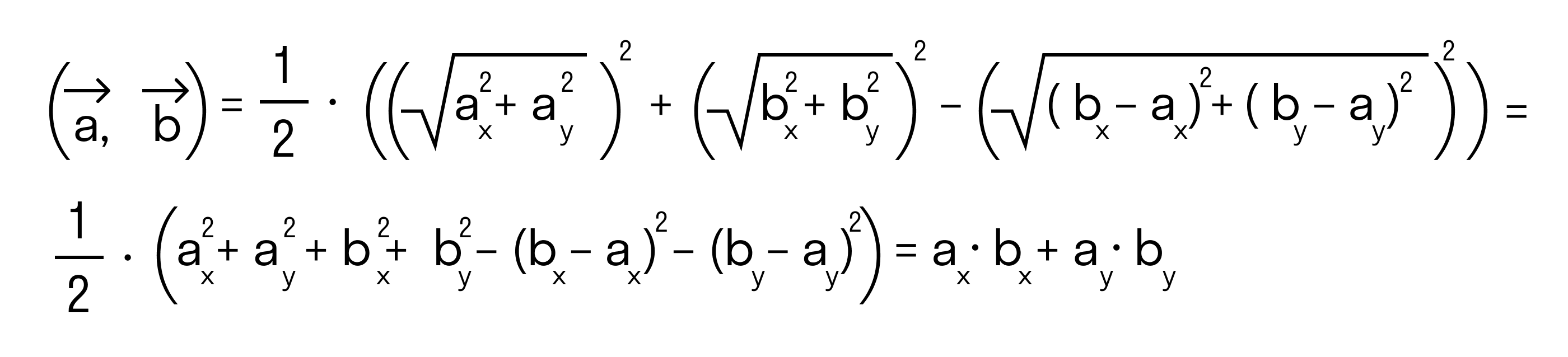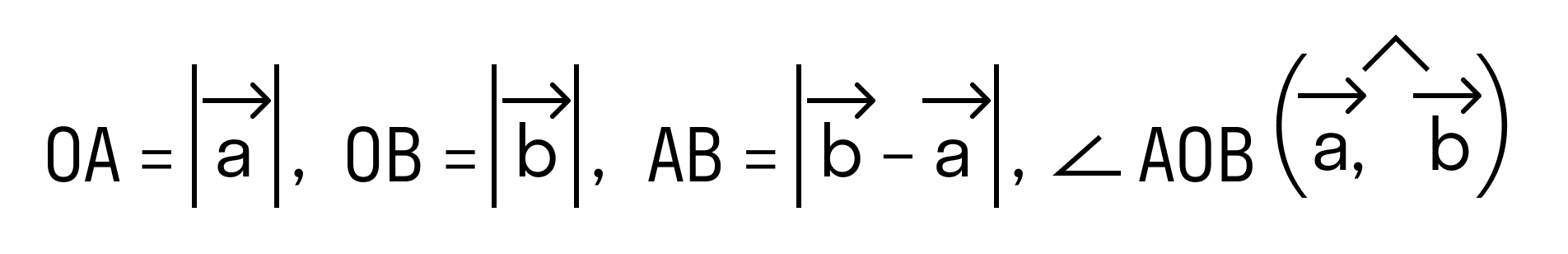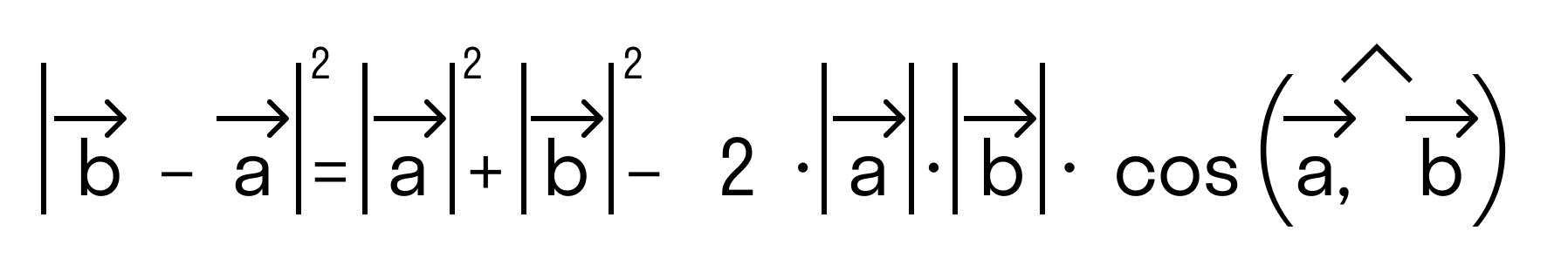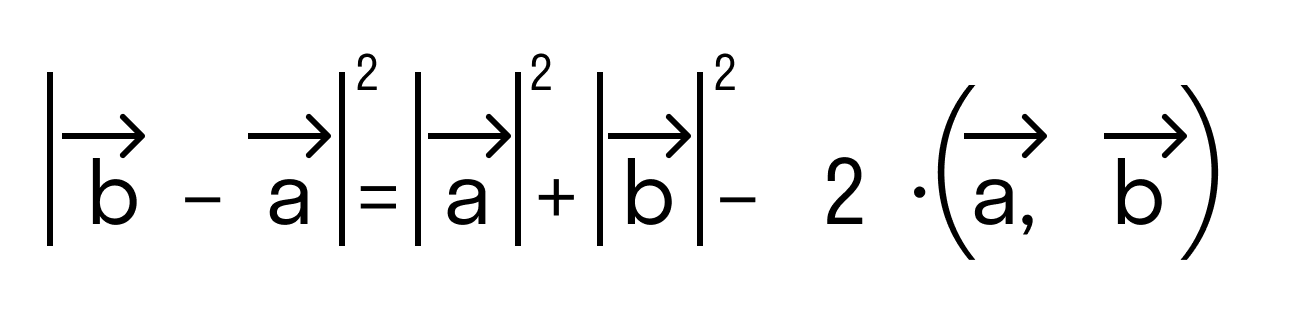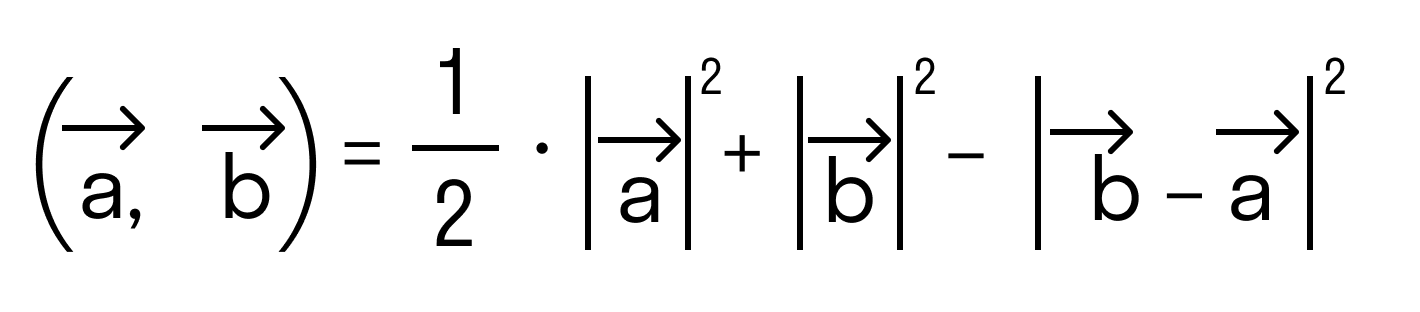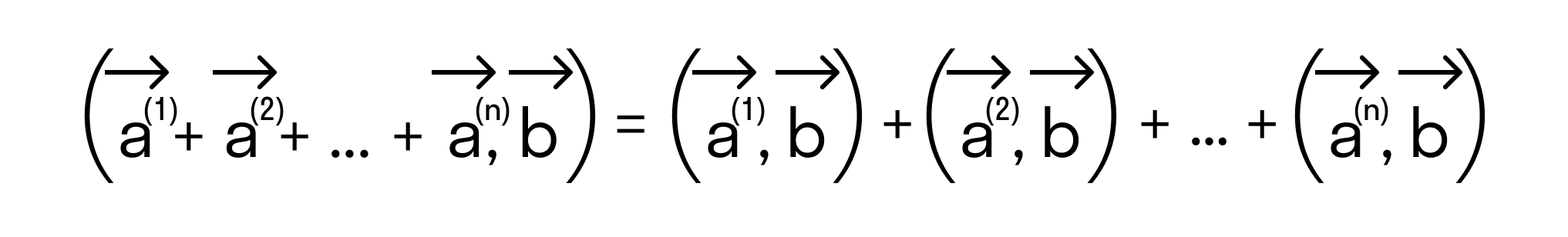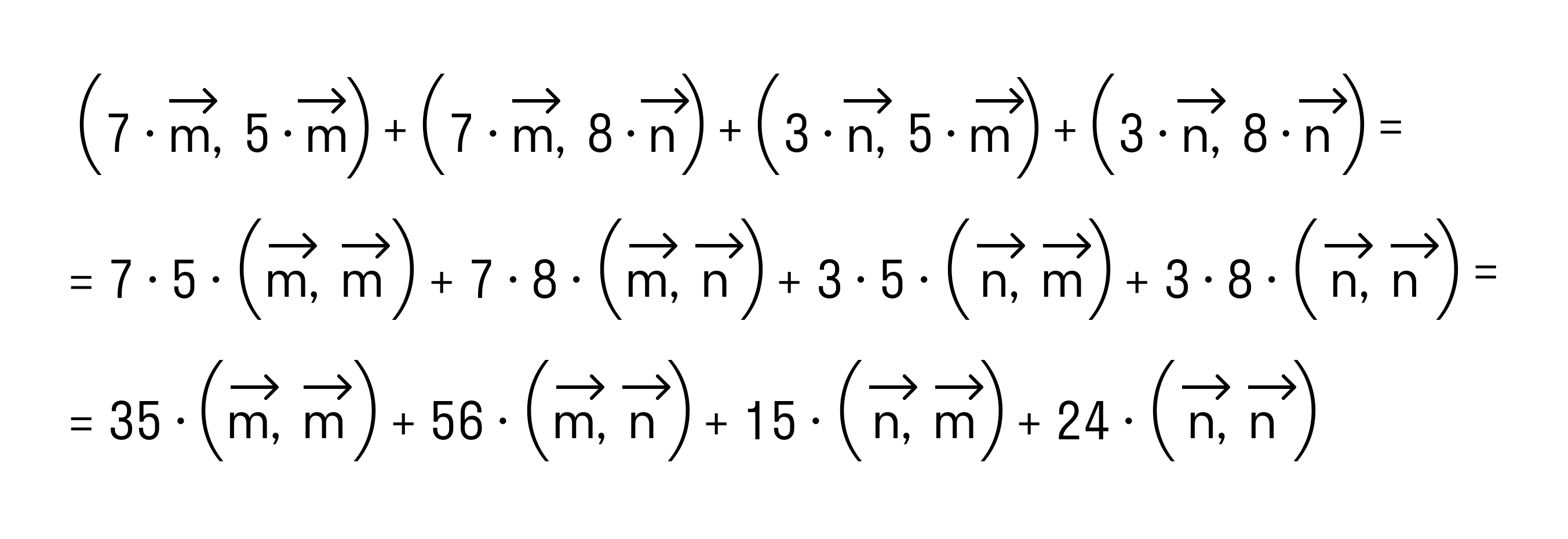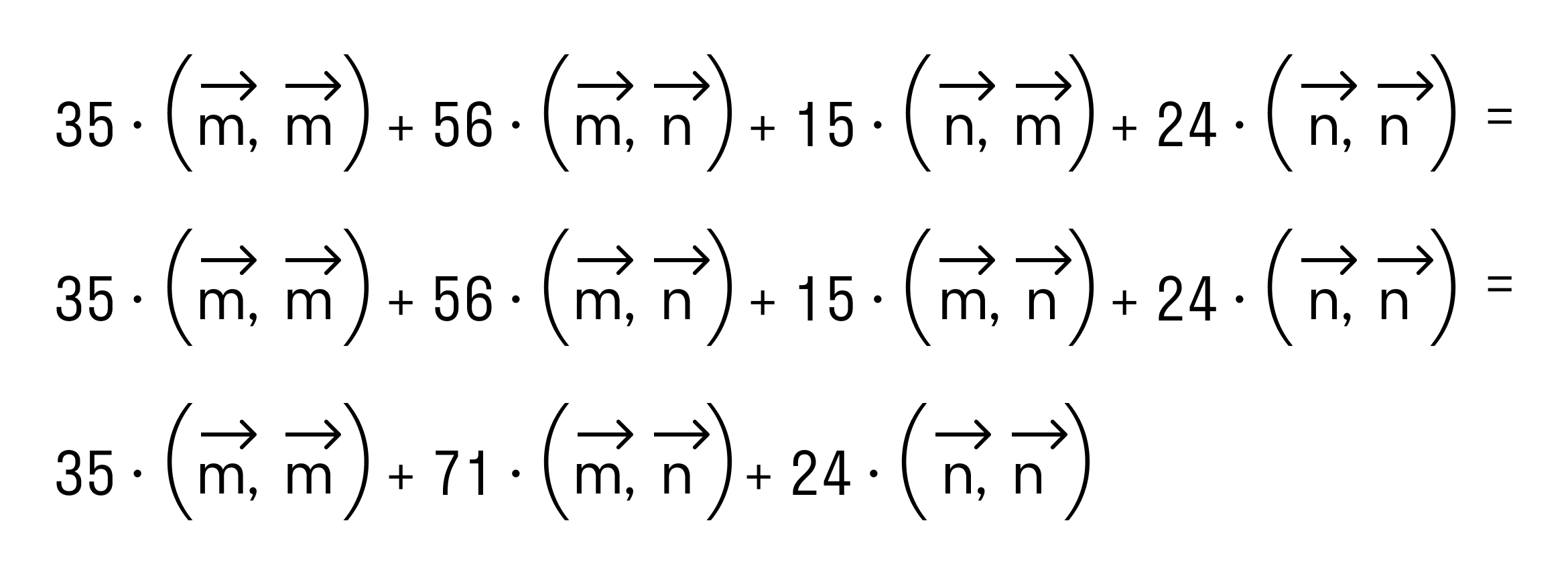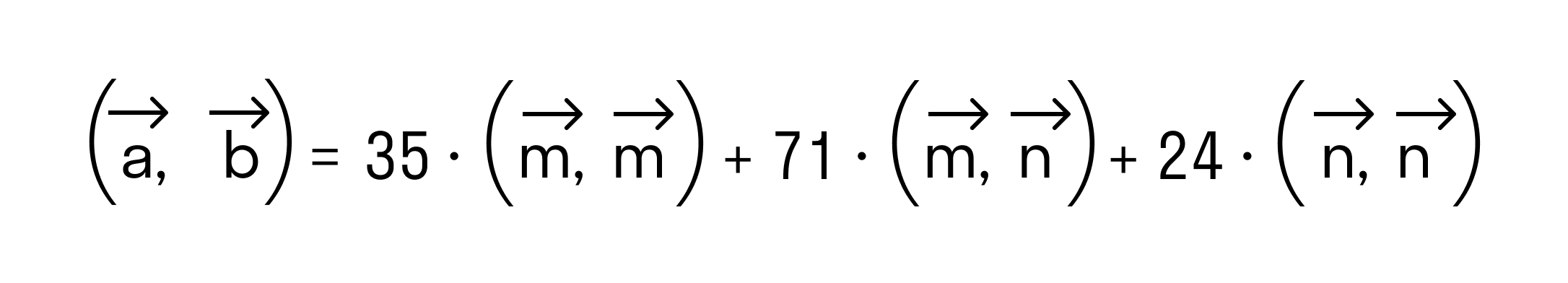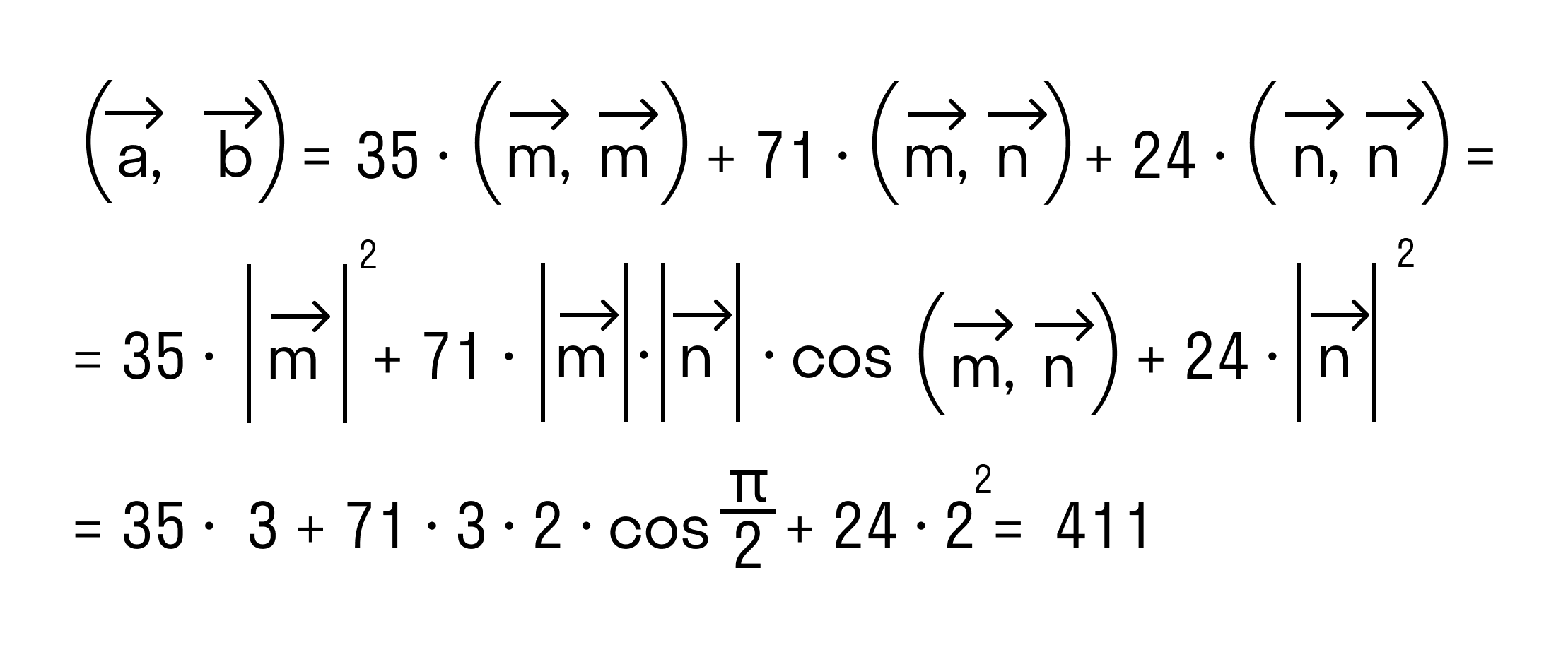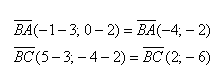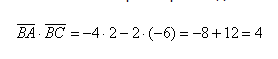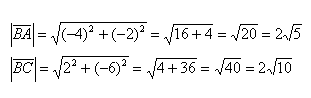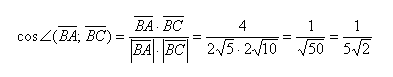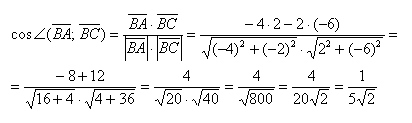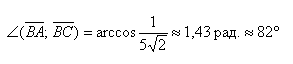Угол между векторами m и n равен 150 градусов

Вопрос по геометрии:

Длины векторов m и n равны 3 и 2. Угол между ними равен 150 градусов. найдите скалярное произведение n(m+n)

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

N(n+m)=n^+mn;
mn=|m|•|n|•cos150=3•2•(-корень из 3/2)=-3 корень из 3;
n(n+m)=4-3 корень из 3

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Угол между векторами | МатематикаСкачать

Длины векторов m и n равны 3 и 2?

Геометрия | 10 — 11 классы

Длины векторов m и n равны 3 и 2.

Угол между ними равен 150 градусов.

Найдите скалярное произведение n(m + n).

mn = |m|•|n|•cos150 = 3•2•( — корень из 3 / 2) = — 3 корень из 3 ;

n(n + m) = 4 — 3 корень из 3.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Скалярное произведение векторов С и D, угол между ними равен 30` и векторы |с| = 3, а |d| = 4, равно ?

Скалярное произведение векторов С и D, угол между ними равен 30` и векторы |с| = 3, а |d| = 4, равно .

Видео:Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

Если скалярное произведение двух векторов равно нулю, то угол между ними составляет 90 градусов?

Если скалярное произведение двух векторов равно нулю, то угол между ними составляет 90 градусов.

Видео:9 класс, 17 урок, Угол между векторамиСкачать

Найдите скалярное произведение векторов а и b, если |а| = 9, |b| = 10, a угол между ними равен 125˚?

Найдите скалярное произведение векторов а и b, если |а| = 9, |b| = 10, a угол между ними равен 125˚.

Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Вычислите скалярное произведение векторов а и b, если | а | = 7, | b | = 8, а угол между ними равен : 45°?

Вычислите скалярное произведение векторов а и b, если | а | = 7, | b | = 8, а угол между ними равен : 45°.

Видео:Угол между векторами. 9 класс.Скачать

Сторона ромба ABCD равна 4 См, угол C равен 60 градусам?

Сторона ромба ABCD равна 4 См, угол C равен 60 градусам.

Найдите скалярное произведение векторов AB и AD.

Видео:Угол между векторами | Геометрия 7-9 класс #100 | ИнфоурокСкачать

Найдите длину векторов 2а + 3в и 2а — 3в , их скалярное произведение и угол между ними, если вектор а (1, — 1, 2) в(2, 2, 0)?

Найдите длину векторов 2а + 3в и 2а — 3в , их скалярное произведение и угол между ними, если вектор а (1, — 1, 2) в(2, 2, 0).

Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Когда скалярное произведение ненулевых векторов а и b положительно?

Когда скалярное произведение ненулевых векторов а и b положительно?

Когда угол м у ними меньше 90 градусов?

Видео:105. Угол между векторамиСкачать

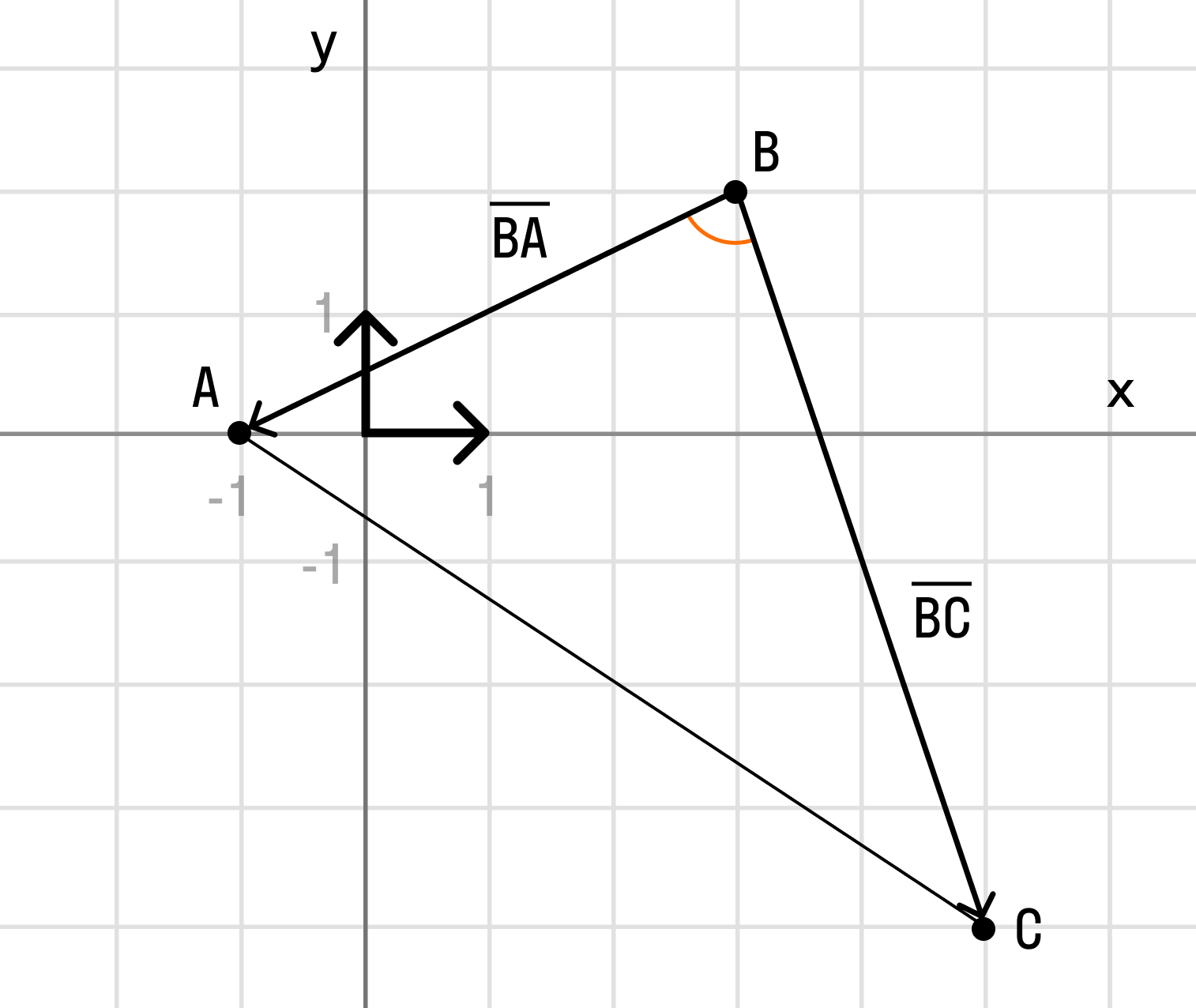
Вычеслите скалярное произведение векторов BA и BC если a = 5 b = 8 а угол между ними равен 60 градусов?

Вычеслите скалярное произведение векторов BA и BC если a = 5 b = 8 а угол между ними равен 60 градусов.

Видео:Скалярное произведение векторов. 9 класс.Скачать

Вычислите скалярное произведение векторов а и b, если | а | = 5, | b | = 8, а угол между ними равен 60 гр?

Вычислите скалярное произведение векторов а и b, если | а | = 5, | b | = 8, а угол между ними равен 60 гр.

Видео:Нахождение угла между векторами через координаты. 9 класс.Скачать

ПОМОГИТЕ ГЕОМЕТРИЯЯЯЯЯЯЯЯЯЯЯЯ?

Если длины двух векторов а и b равны ΙаΙ = 2, ΙbΙ = 5, а угол между ними равен 45°, найти скалярное произведение этих векторов.

Вы находитесь на странице вопроса Длины векторов m и n равны 3 и 2? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Ну ок 2, 8 первый и 12, 8 второй.

Пожалуйста вот ничего сложного.

Сечение конуса по образующим — равносторонний треугольник, так как угол при основании равен 60°. Тогда высота конуса по формуле h = a * √3 / 2 получим h = 4, 5√3см. Второй вариант : Высота конуса — это катет прямоугольного треугольника, лежащий про..

Видео:Угол между векторами. Уроки 11. Геометрия 9 классСкачать

Скалярное произведение векторов

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.

Видео:100 тренировочных задач #135 Угол между векторамиСкачать

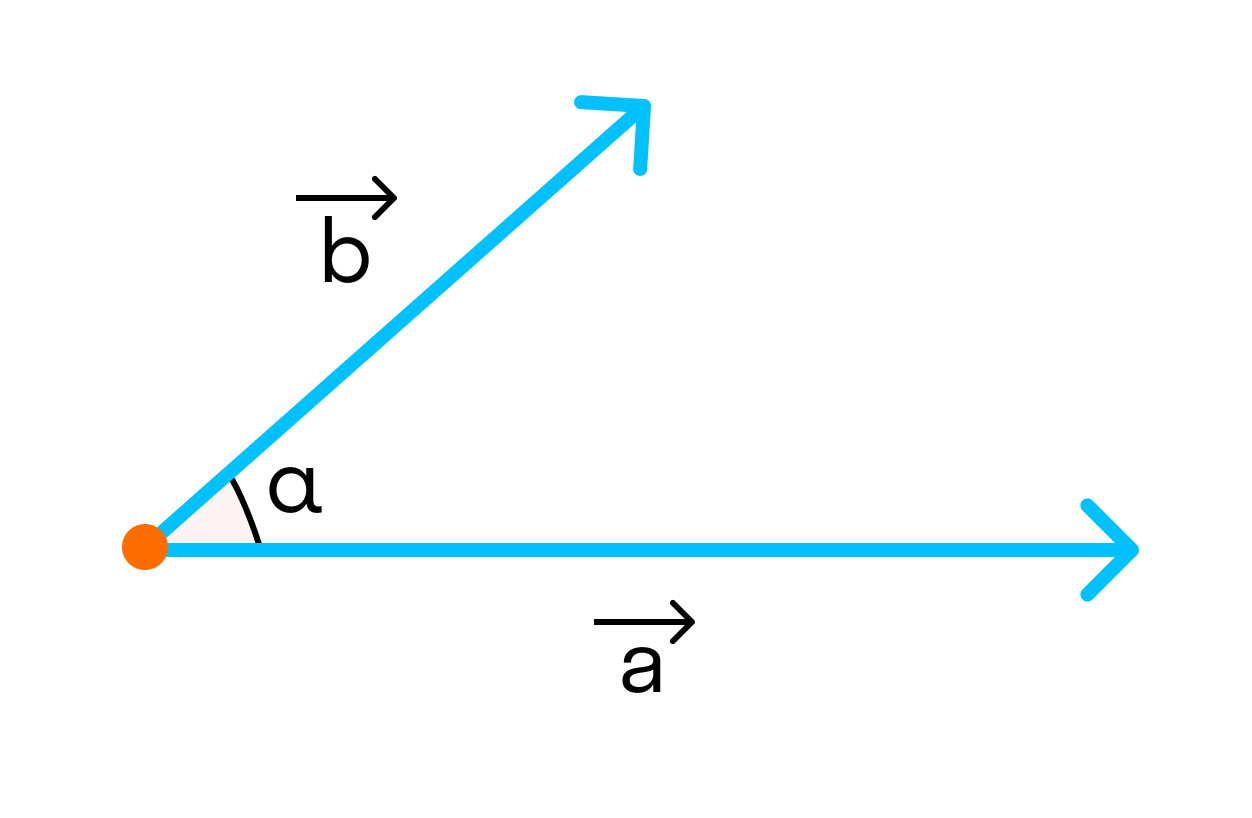
Угол между векторами

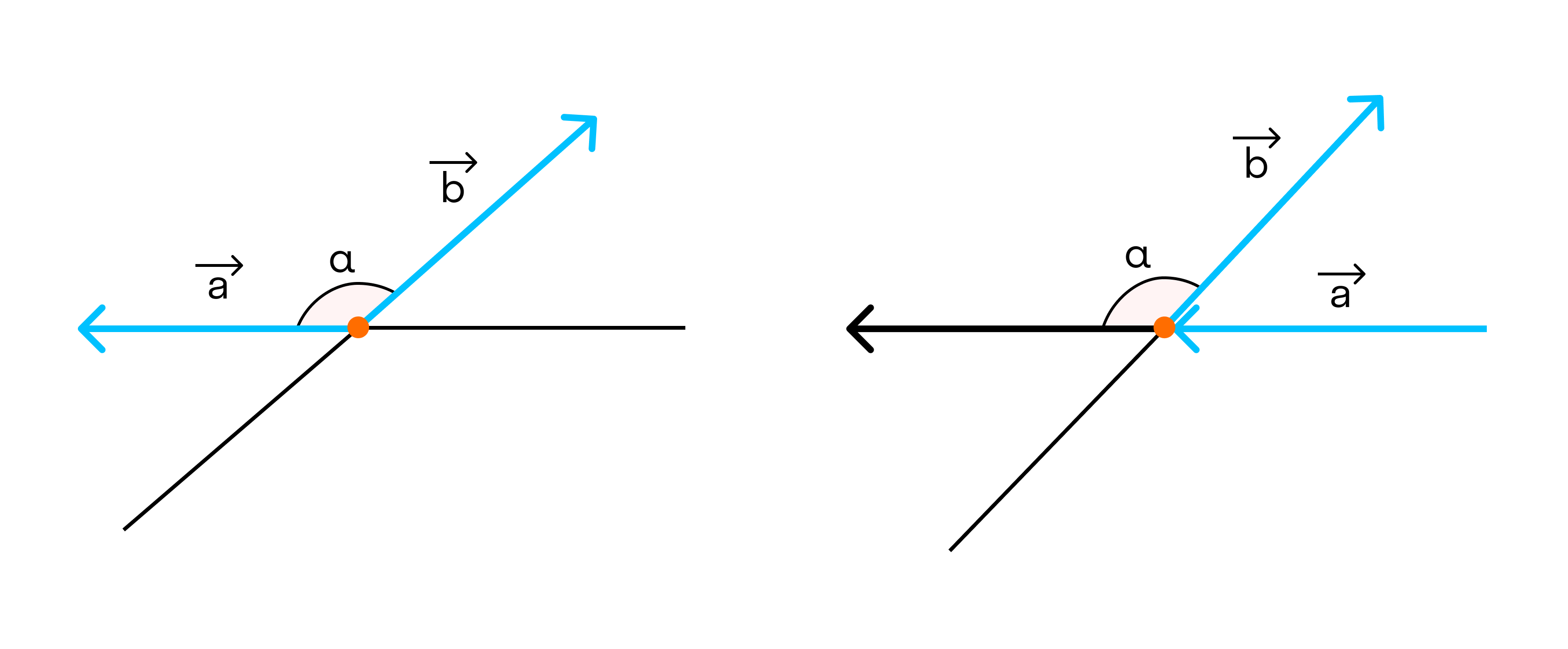
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=

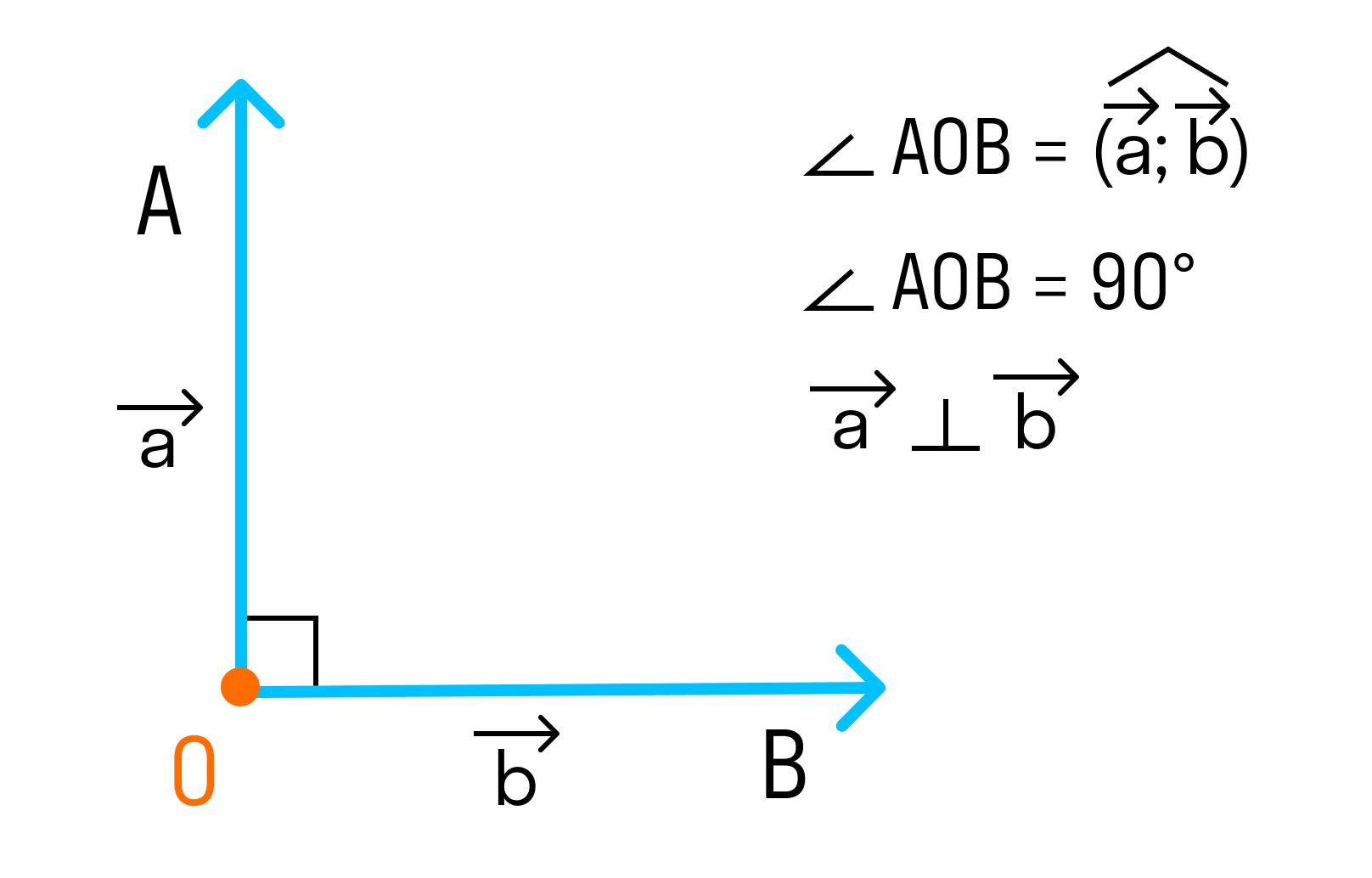
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.

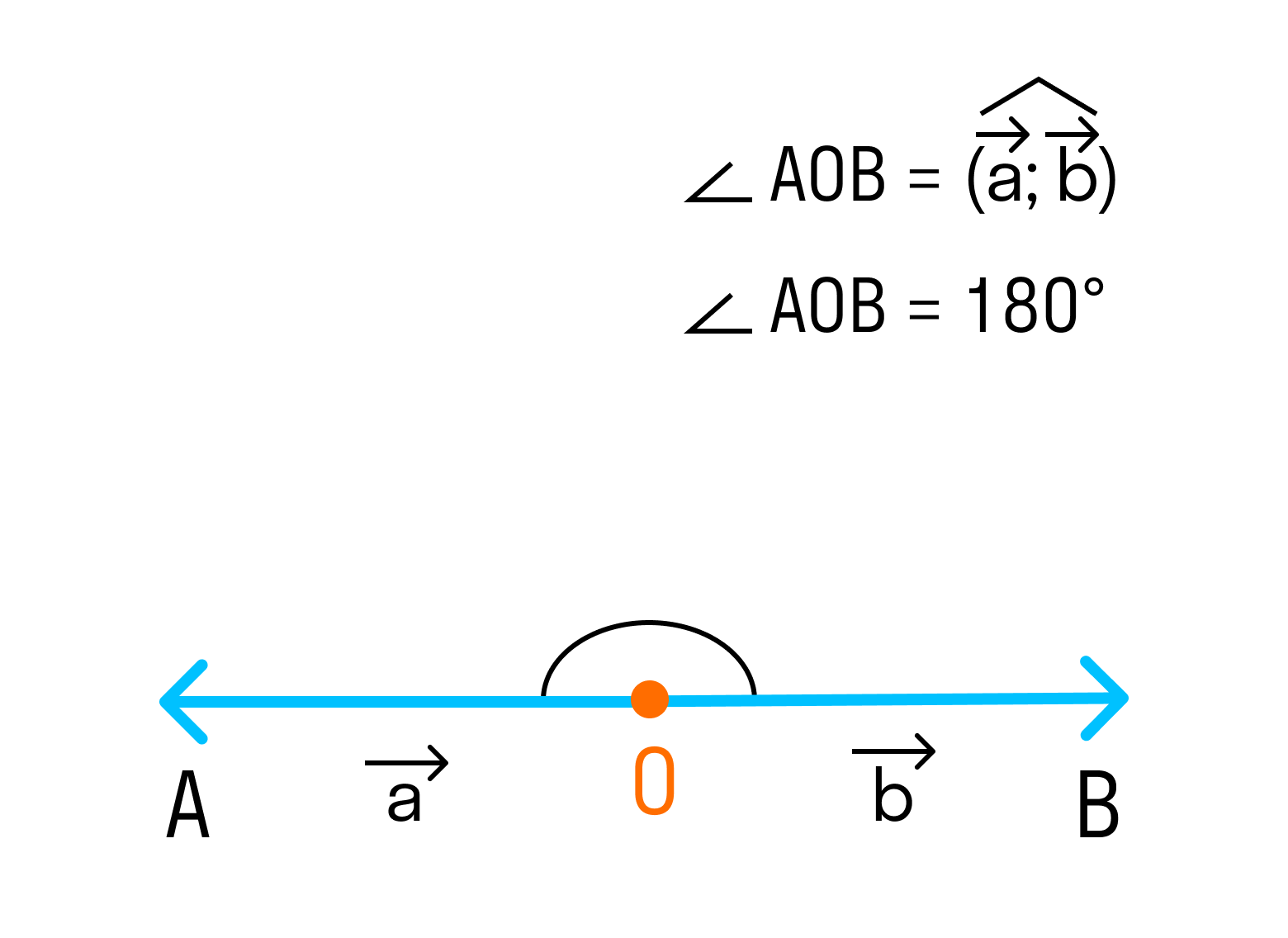
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.

Также векторы могут образовывать тупой угол. Это выглядит так:

Видео:найти угол между единичными векторамиСкачать

Скалярное произведение векторов

Определение скалярного произведения можно сформулировать двумя способами:

Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.

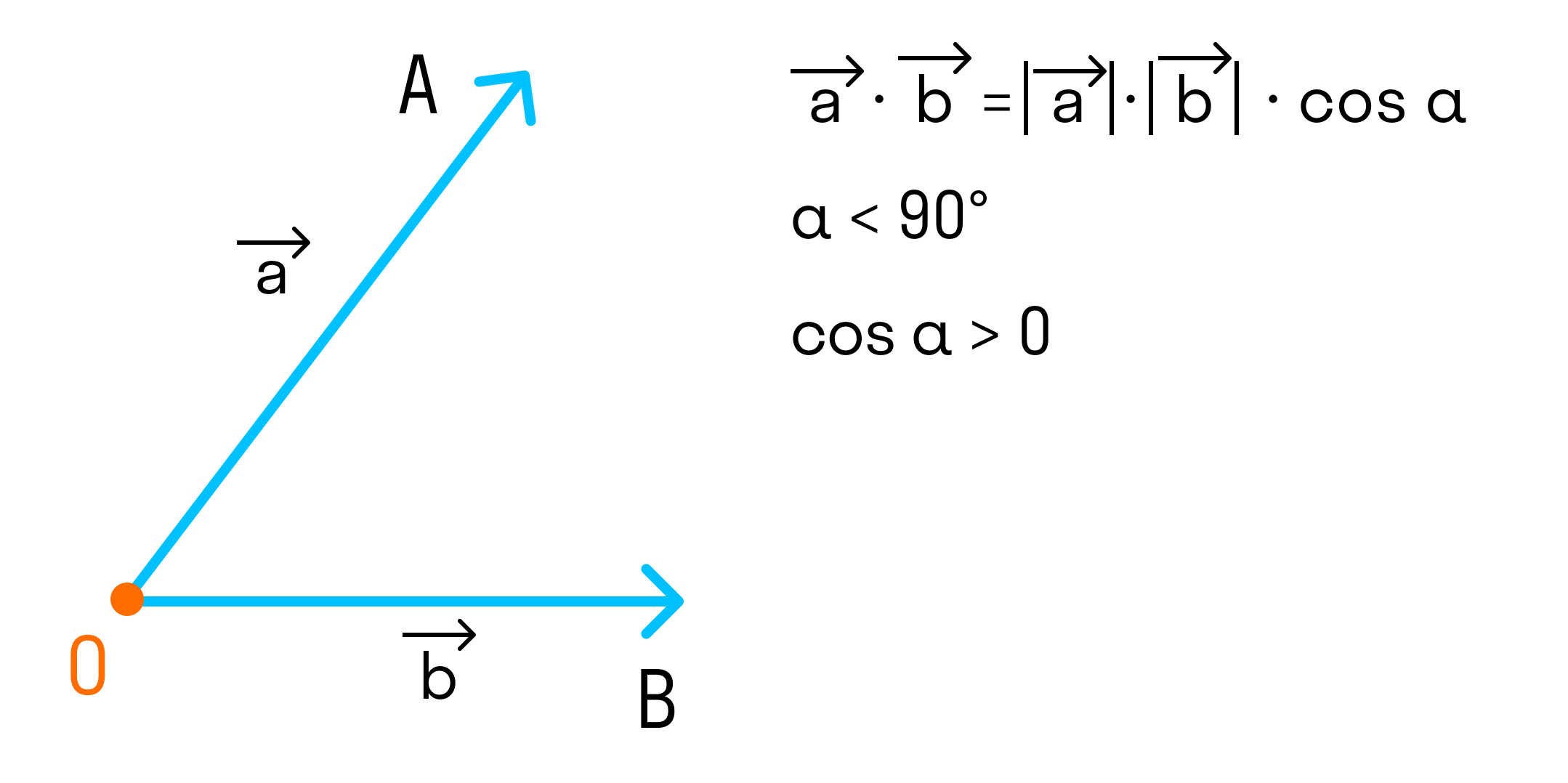
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:

→a * →b = →|a| * →|b| * cosα

Что важно запомнить про геометрическую интерпретацию скалярного произведения:

• Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
• Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα

Видео:11 класс, 5 урок, Угол между векторамиСкачать

Скалярное произведение в координатах

Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.

То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by

А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz

Докажем это определение:

Сначала докажем равенства

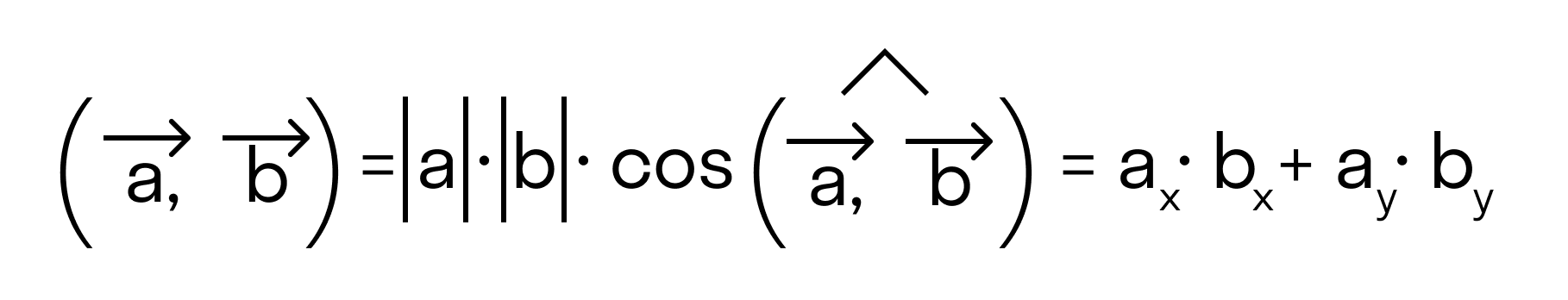
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)

Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)

Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:

то последнее равенство можно переписать так:

а по первому определению скалярного произведения имеем

Вспомнив формулу вычисления длины вектора по координатам, получаем

Записывайтесь на наши курсы по математике для учеников с 1 по 11 классы!

Видео:ГЕОМЕТРИЯ 11 класс : Угол между векторами. Скалярное произведение векторовСкачать

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В плоской задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by

Формула скалярного произведения векторов для пространственных задач

В пространственной задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by + az * bz

Формула скалярного произведения n-мерных векторов

В n-мерном пространстве скалярное произведение векторов a = и b = можно найти по формуле:

a * b = a1 * b1 + a2 * b2 + . + an * bn

Видео:№1039. Диагонали квадрата ABCD пересекаются в точке О. Найдите угол между векторами: а) АВ и АССкачать

Свойства скалярного произведения

Свойства скалярного произведения векторов:

Скалярное произведение вектора самого на себя всегда больше или равно нулю. В результате получается нуль, если вектор равен нулевому вектору.

→0 * →0 = 0

Скалярное произведение вектора самого на себя равно квадрату его модуля:

→a * →a = →∣∣a∣∣2

Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:

→a * →b = →b * →a

Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:

(→a + →b) * →c = →a * →c + →b * →c

Сочетательный закон для скалярного произведения:

(k * →a) * →b = k * (→a * →b)

Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:

a ≠ 0, b ≠ 0, a * b = 0 a ┴ b

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)

По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.

Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,

Видео:СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ \\ 9 класс \\ геометрияСкачать

Примеры вычислений скалярного произведения

Пример 1.

Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.

У нас есть все данные, чтобы вычислить скалярное произведение по определению:

(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.

Ответ: (→a,→b) = 21/2 = 10,5.

Пример 2.

Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.

Используем формулу →a * →b = →|a| * →|b| * cosα.

В данном случае:

→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3

Пример 3.

Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.

По свойству дистрибутивности скалярного произведения имеем

Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:

В силу свойства коммутативности последнее выражение примет вид

Итак, после применения свойств скалярного произведения имеем

Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:

Пример 4.

В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.

Введем систему координат.

Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.

Найдем координаты векторов →AB1 и →BC1:

Найдем длины векторов →AB1 и →BC1:

Найдем скалярное произведение векторов →AB1 и →BC1:

Найдем косинус угла между прямыми AB1 и BC1:

Пример 5.

а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .

б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).

а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно

б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)

Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.

Обратите внимание на два существенных момента:

• В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
• В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.

Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.

Пример 6.

Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.

По условию чертеж выполнять не требуется, но для удобства можно сделать:

Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.

Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).

Вычислим скалярное произведение:

Вычислим длины векторов:

Найдем косинус угла:

Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:

Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.

Найдём сам угол:

Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.

Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°

Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.

А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.

🔍 Видео

Угол между векторамиСкачать