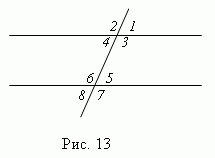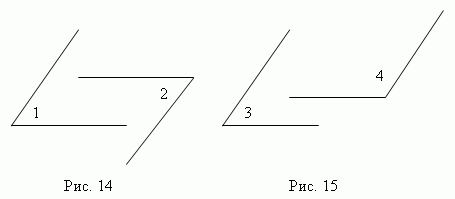Для того чтобы мы могли определить угол между двумя лучами, они вовсе необязательно должны иметь общее начало. В самом деле, каждый луч, независимо от того, где он начинается, задает какое-то направление на плоскости, а различие между двумя направлениями характеризуется не чем иным, как углом — точнее говоря, угловым расстоянием или, с учетом знака, угловым смещением.
Рассмотрим лучи OА и OВ с общим началом в точке O. Обозначим угол между ними через γ . Давайте, однако, договоримся, что здесь и далее в этих рассуждениях под «углом» мы будем понимать не угловое расстояние, а угловое смещение, которое может быть положительным или отрицательным. Об этом на рисунках нам будет напоминать стрелка у дуги, обозначающей угол:
Пусть на луче OA между O и A задана произвольная точка A0, а на луче OB между O и B — произвольная точка B0. Очевидно, что угол между лучами A0A и B0B тоже равен γ , хотя на этот раз лучи исходят не из одной точки.
Этот угол мы могли бы найти и другим способом. Проведем через точки A0 и B0 прямую и отметим на ней точки A1 и B1, как показано на рисунке:
Измерим углы ∠A1A0A и ∠A1B0B и обозначим результаты наших измерений через α и β соответственно. Эти углы (а точнее — угловые смещения) отсчитываются от одного и того же направления, задаваемого лучом B0A1. Очевидно, что угол γ можно вычислить как
Пусть теперь на плоскости нам даны два произвольных луча B0B и A0A. Опираясь на предыдущие рассуждения, мы всегда можем найти угол γ между ними одним из следующих двух способов.
Первый способ. Восстановить исходные лучи до полных прямых, найти точку их пересечения и непосредственно измерить угол γ между подходящими лучами, начинающимися в этой точке:
Второй способ. Провести прямую через точки A0 и B0, измерить образовавшиеся углы α и β и вычислить угол γ по формуле γ = β − α .
Необходимо отметить, что второй способ работает всегда, а с первым способом могут возникнуть проблемы. Это случается, в частности, тогда, когда углы α и β в точности равны друг другу:
В этом случае угол γ , вычисляемый по формуле γ = β − α , обращается в нуль. А это означает, что прямые, восстановленные из лучей B0B и A0A, нигде не пересекаются.
Действительно, если бы они пересекались, то угол γ можно было бы измерить в точке пересечения непосредственно, но тогда он оказался бы отличен от нуля.
Пусть две несовпадающие прямые принадлежат одной плоскости и на них лежат лучи, угол между которыми равен нулю. Про такие прямые говорят, что они параллельны друг другу. Важнейшее свойство параллельных прямых заключается в том, что они нигде не пересекаются.
Вернемся к задаче о нахождении угла γ между двумя произвольными лучами B0B и A0A с началом в разных точках. Мы только что рассмотрели особый случай, когда этот угол равен нулю. Про лучи, угловое расстояние между которыми равно нулю, говорят, что они сонаправлены или параллельны. Возможен другой особый случай, когда угол γ , рассчитанный по формуле γ = β − α , оказывается равен 180° или −180°:
Такие лучи называются противонаправленными или антипараллельными. Несложно видеть, что прямые, восстановленные из этих лучей, параллельны друг другу и, таким образом, этот случай очень похож на предыдущий.
Постороение параллельных прямых
Пусть на листе бумаги начерчена некоторая прямая n и мы хотим провести другую прямую, параллельную первой. Делается это так. Совместим с прямой n одну из сторон чертежного треугольника. К другой стороне треугольника приставим линейку. Прочно держим линейку одной рукой и передвигаем треугольник другой рукой, скользя им вдоль линейки. После этого проводим линию по той стороне треугольника, которую первоначально мы приставляли к исходной прямой n. Новая линия образует тот же угол с линейкой, что и прямая n, а значит, обе линии параллельны друг другу.
Если мы хотим, чтобы новая прямая прошла через какую-то определенную точку, то мы всегда это может сделать, остановив скольжение угольника вдоль линейки в подходящем месте.
- Угол между прямыми онлайн
- Предупреждение
- 1. Угол между прямыми на плоскости
- Прямые заданы каноническими уравнениями
- 1.1. Определение угла между прямыми
- 1.2. Условие параллельности прямых
- 1.3. Условие перпендикулярности прямых
- Прямые заданы общими уравнениями
- 1.4. Определение угла между прямыми
- 1.5. Условие параллельности прямых
- 1.6. Условие перпендикулярности прямых
- 2. Угол между прямыми в пространстве
- 2.1. Определение угла между прямыми
- 2.2. Условие параллельности прямых
- 2.3. Условие перпендикулярности прямых
- Параллельные прямые
- 💥 Видео
Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
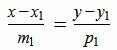 , , | (1.1) |
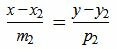 , , | (1.2) |
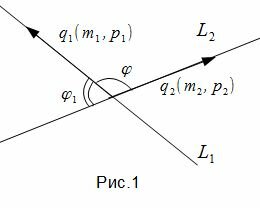
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
 , , |
 , , | (1.3) |
Из выражения (1.3) получим:
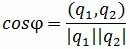 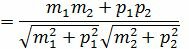 . . | (1.4) |
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
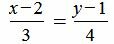 . . | (1.5) |
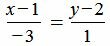 . . | (1.6) |
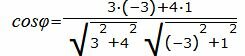 . . |
Упростим и решим:
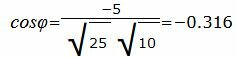 . . |
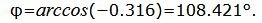 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
 |
Угол между прямыми равен:
 |
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
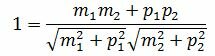 . . | (1.7) |
Сделаем преобразования с выражением (1.7):
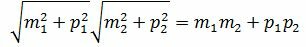 , , |
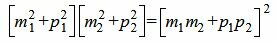 , , |
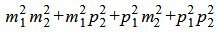 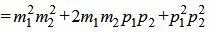 , , |
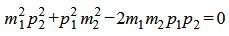 , , |
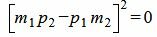 , , |
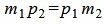 . . | (1.8) |
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
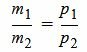 . . | (1.9) |
Пример 2. Определить, параллельны ли прямые
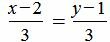 . . | (1.10) |
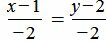 . . | (1.11) |
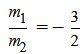 , , 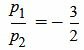 . . |
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
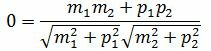 . . | (1.12) |
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
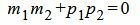 . . | (1.13) |
Пример 3. Определить, перпендикулярны ли прямые
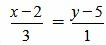 | (1.14) |
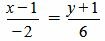 . . | (1.15) |
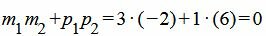 . . | (16) |
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
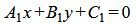 | (1.17) |
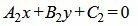 . . | (1.18) |
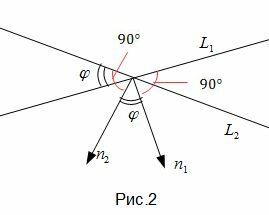
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
 . . |
Из определения скалярного произведения двух векторов, имеем:
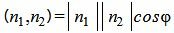 . . | (1.19) |
Из уравнения (19) получим
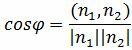 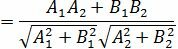 . . | (1.20) |
Пример 4. Найти угол между прямыми
| 5x1−2x2+3=0 | (1.21) |
| x1+3x2−1=0. | (1.22) |
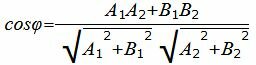 | (23) |
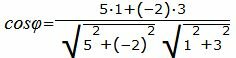 |
Упростим и решим:
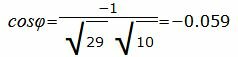 |
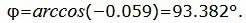 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
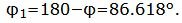 |
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
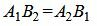 . . | (1.24) |
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
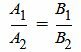 . . | (1.25) |
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
| 4x+2y+2=0 | (1.26) |
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
| A1A2+B1B2=0. | (1.28) |
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
| 4x−1y+2=0 | (1.29) |
| 2x+8y−14=0. | (1.30) |
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
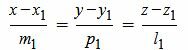 , , | (2.1) |
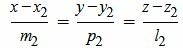 , , | (2.2) |
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
 , , | (2.3) |
Из выражения (2.3) получим:
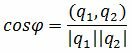 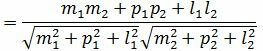 . . | (2.4) |
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
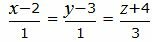 . . | (2.5) |
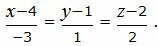 | (2.6) |
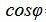 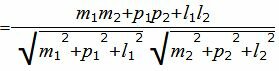 . . |
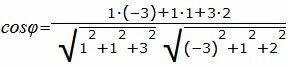 . . |
Упростим и решим:
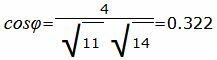 . . |
 |
Угол между прямыми равен:
 |
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
| m1=αm2, p1=αp2, l1=αl2 | (2.7) |
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
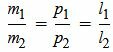 | (2.8) |
Отметим, что любую пропорцию 
Пример 2. Определить, параллельны ли прямые
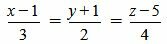 . . | (2.9) |
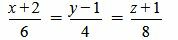 . . | (2.10) |
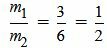 , , 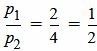 , , 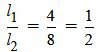 . . |
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
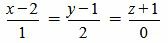 . . | (2.11) |
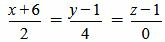 . . | (2.12) |
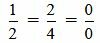 . . | (2.13) |
Выражение (2.13) нужно понимать так:
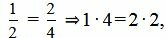 , , 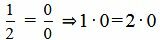 , , 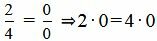 . . | (2.14) |
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
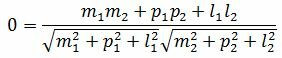 . . | (2.15) |
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
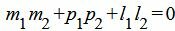 . . | (2.16) |
Пример 3. Определить, перпендикулярны ли прямые
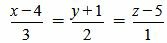 | (2.17) |
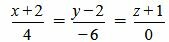 . . | (2.18) |
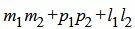 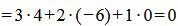 . . | (2.19) |
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Видео:Расстояние между параллельными прямымиСкачать

Параллельные прямые
Параллельные прямые . Расстояние между параллельными прямыми .
Углы с соответственно параллельными сторонами .
Соответственные углы .
Внутренние и внешние накрест лежащие углы .
Внутренние и внешние односторонние углы .
Углы с соответственно перпендикулярными сторонами .
Пропорциональные отрезки . Теорема Фалеса.
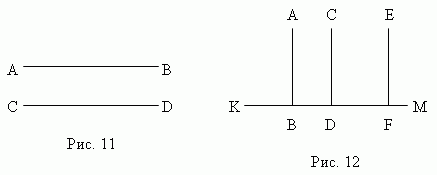
Две прямые AB и CD ( рис.11 ) называются параллельными , если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать. Обозначение: AB || CD . Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой. Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Угол между двумя параллельными лучами равен нулю, если у них одинаковые направления, и 180 ° , если их направления противоположны. Все перпендикуляры ( AB , CD , EF , рис.12 ) к одной и той же прямой KM параллельны между собой. Обратно, прямая KM , перпендикулярная к одной из параллельных прямых, перпендикулярна и к остальным. Длина отрезка перпендикуляра, заключённого между двумя параллельными прямыми, есть расстояние между ними.
При пересечении двух параллельных прямых третьей прямой, образуются восемь углов ( рис.13 ), которые попарно называются:
1) соответственные углы ( 1 и 5; 2 и 6; 3 и 7; 4 и 8 ); эти углы попарно
равны: (







2) внутренние накрест лежащие углы ( 4 и 5; 3 и 6 ); они попарно равны;
3) внешние накрест лежащие углы ( 1 и 8; 2 и 7 ); они попарно равны;
4) внутренние односторонние углы ( 3 и 5; 4 и 6 ); их сумма равна 180 °
( 



5) внешние односторонние углы ( 1 и 7; 2 и 8 ); их сумма равна 180 °
( 



Углы с соответственно параллельными сторонами либо равны друг другу ( если они оба острые, или оба тупые, 



Углы с соответственно перпендикулярными сторонами также либо равны друг другу ( если они оба острые, или оба тупые ), либо их сумма равна 180 ° .
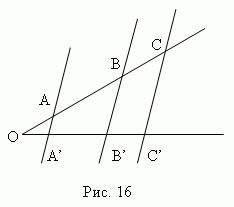
Теорема Фалеса. При пересечении сторон угла параллельными прямыми ( рис.16 ) стороны угла делятся на пропорциональные отрезки:
Copyright © 2004 — 2007 Др. Юрий Беренгард. All rights reserved.
💥 Видео
Угол между прямыми в пространстве. 10 класс.Скачать

№557. Стороны угла А пересечены параллельными прямыми ВС и DE, причем точки В и D лежатСкачать

Пары углов в геометрииСкачать

14. Угол между прямыми в пространствеСкачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Углы между секущими и параллельными прямымиСкачать

9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать

9. Угол между прямымиСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

10 класс, 9 урок, Угол между прямымиСкачать

Параллельные прямые (задачи).Скачать

Угол между прямыми!Скачать

19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать