Угол между хордой и касательной к окружности равен 48 (3 видео)

Задание 16 из ОГЭ по математике

Два угла четырёхугольника, вписанного в окружность, равны $93^°$ и $54^°$ (см. рис.). Найдите больший из оставшихся углов. Ответ дайте в градусах.

Угол между хордой $AB$ и касательной $BC$ к окружности равен $48^°$ (см. рис.). Найдите величину меньшей дуги, стягиваемой хордой $AB$. Ответ дайте в градусах.

Четырёхугольник $ABCD$ вписан в окружность, причём угол $A$ больше угла $C$ в два раза (см. рис.). Найдите угол $A$. Ответ дайте в градусах.

Четырёхугольник $ABCD$ вписан в окружность, причём угол $B$ равен $87^°$ (см. рис.). Найдите угол $D$. Ответ дайте в градусах.

Точка $O$ — центр окружности, на которой лежат точки $P$, $K$ и $F$. Известно, что $∠ POF=95^°$ и $∠ POK=143^°$ (см. рис.). Найдите дугу $KF$, если она меньше $150^°$. Ответ дайте в градусах.

Колесо имеет $32$ спицы. Найдите величину угла (в градусах), который образуют две соседние спицы.

В треугольнике $ABC$ угол $C$ равен $90^°$, $AB=13$, $BC=5$ (см. рис.). Найдите радиус вписанной окружности.

Два угла вписанного в окружность четырёхугольника равны $75^°$ и $92^°$ (см. рис.). Найдите меньший из оставшихся углов. Ответ дайте в градусах.

Хорда $AB$ стягивает дугу окружности в $92^°$ (см. рис.). Найдите угол $ABC$ между хордой и касательной к окружности, проведённой через точку $B$. Ответ дайте в градусах.

В треугольнике $ABC$ $AC=25$,
$BC=10√ $, угол $C$ равен $90^°$. Найдите радиус описанной окружности этого треугольника.

Радиус окружности с центром в точке $O$ равен $17$, а длина хорды $AB$ равна $30$. Найдите расстояние от хорды $AB$ до параллельной ей касательной $m$ (см. рис.).

Прямая касается окружности в точке $P$. Точка $O$ — центр окружности. Хорда $PR$ образует с касательной угол, равный $57^°$ (см. рис.). Найдите величину угла $ORP$.

$AC$ и $BD$ — диаметры окружности с центром в точке $O$. Угол $ACB$ равен $68^°$. Найдите угол $AOD$. Ответ дайте в градусах.

$AC$ и $BD$ — диаметры окружности с центром в точке $O$. Центральный угол $AOB$ равен $140^°$. Найдите угол $BAC$. Ответ дайте в градусах.

Через точку $A$, лежащую на окружности с центром в точке $O$, проведена касательная $AB$. Отрезок $BO$ пересекает окружность в точке $D$ (см. рис.). Найдите диаметр окружности, если $AB=60$, $BD=20$.…

К окружности с центром в точке $O$ проведены касательная $FK$ и секущая $FO$, пересекающая окружность в точке $E$. Найдите $FE$, если $FK=50$, $OE=120$ (см. рис.).

На отрезке $AB$ выбрана точка $K$ так, что $AK=8$, $BK=9$. Построена окружность с центром $A$, проходящая через $K$ (см. рис.). Луч, выходящий из точки $B$, касается окружности в точке $M$. Найдит…

Диаметр окружности равен $20$, а расстояние от центра окружности до хорды равно $6$ (см. рис.). Найдите длину хорды.

Длина хорды равна $24$, а расстояние от центра окружности до этой хорды равно $5$ (см. рис.). Найдите диаметр окружности.

В окружности проведены две пересекающиеся хорды $AB$ и $CD$. Известно, что дуга $AD$ равна $40^°$, а угол $ADC$ равен $60^°$ (см. рис.). Найдите угол $DBC$. Ответ дайте в градусах.

Видео:Угол между хордой и касательной. 9 класс.Скачать

Угол между хордой AB и касательной BC

27878. Угол между хордой AB и касательной BC к окружности равен 32 0 . Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Градусная мера искомой дуги соответствует углу АОВ. Угол между радиусом окружности и касательной проходящей через общую точку равен 90 0 , значит мы можем найти:

Треугольник ОВА равнобедренный, следовательно

Проект «МатематикаЕГЭ» — Решение задач из открытого банка заданий ЕГЭ

Видео:Угол между хордой и касательнойСкачать

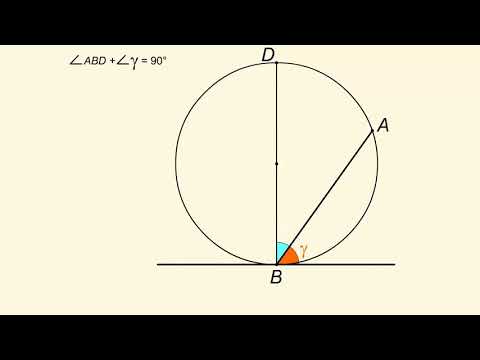
Угол между касательной и хордой

Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

Касательная перпендикулярна радиусу, проведенному в точку касания.

Пусть . Тогда . Треугольник ОСА – равнобедренный, ОА = ОС (как радиусы окружности). Значит, , что и требовалось доказать.

Заметим, что – как вписанный, опирающийся на ту же дугу.

Задача ЕГЭ по теме «Угол между касательной и хордой»

Угол между хордой AB и касательной BC к окружности равен . Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Касательная ВС перпендикулярна радиусу ОВ, проведенному в точку касания. Значит, угол ОВС равен 90°, и тогда угол ОВА равен . Угол ОАВ также равен 58°, так как треугольник ОАВ – равнобедренный, его стороны ОА и ОВ равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол АОВ, равен .

Центральный угол равен угловой величине дуги, на которую он опирается, и тогда дуга АВ равна .

Эту задачу можно решить быстрее, зная теорему об угле между касательной и хордой.
Угол между касательной и хордой, проведенной через точку касания, — это угол АВС. Он равен половине угловой величины дуги, заключенной между касательной ВС и хордой АВ, то есть дуги АВ. Значит, дуга АВ равна .