Угол 630 на окружности

Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы.

Углы 0°,30°,45°,60°,90°,180°270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Sin, Cos, tg, ctg.

Раздел: Таблицы численных значений + Таблицы Брадиса:

Углы в окружности, центральный и вписанный. Свойства и способы нахождения

Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?

Что такое центральный угол?

Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).

Вам будет интересно: Пурпурные бактерии — описание, особенности и интересные факты

Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.

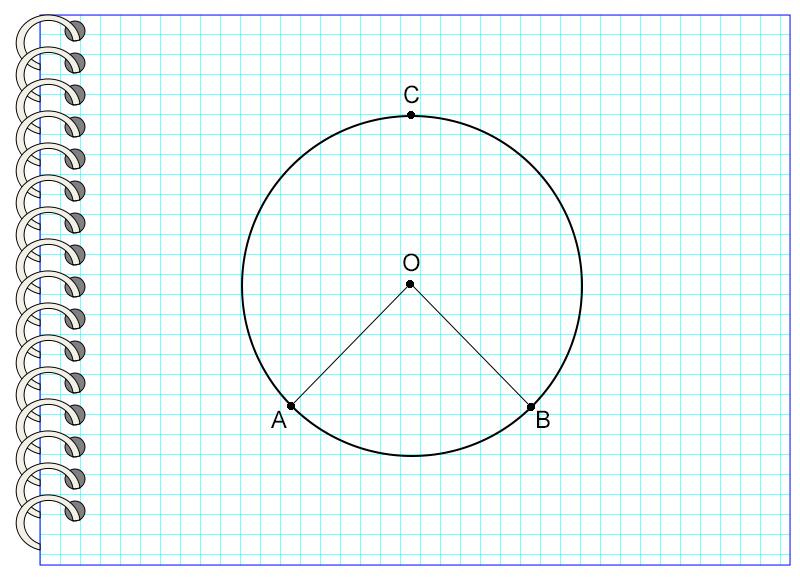
Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.

Рассмотрим пример №1.

На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О. Он опирается на дугу AB, не содержащую точку С.

Чем вписанный угол отличается от центрального?

Вам будет интересно: Площадь боковой поверхности и объем усеченной пирамиды: формулы и пример решения типовой задачи

Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.

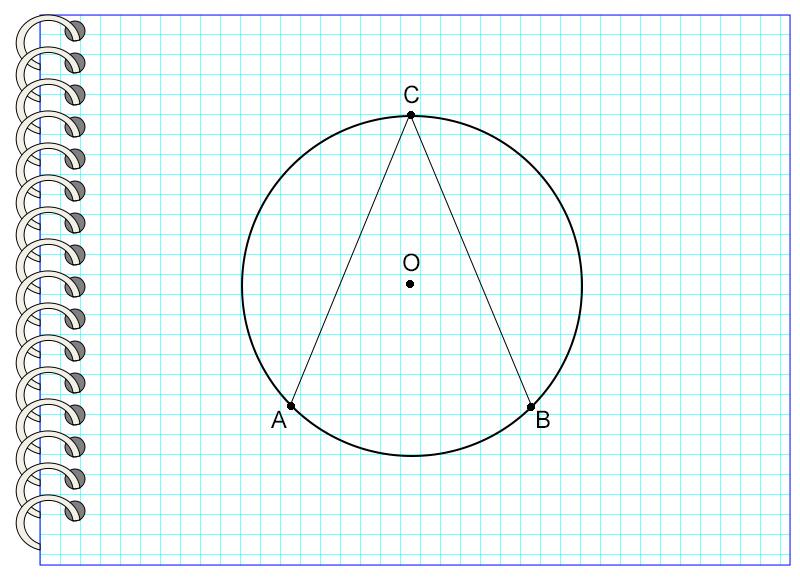
Приведем следующий пример.

Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.

Чему равен центральный угол

Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.

Вам будет интересно: Профиль крыла самолета: виды, технические и аэродинамические характеристики, метод расчета и наибольшая подъемная сила

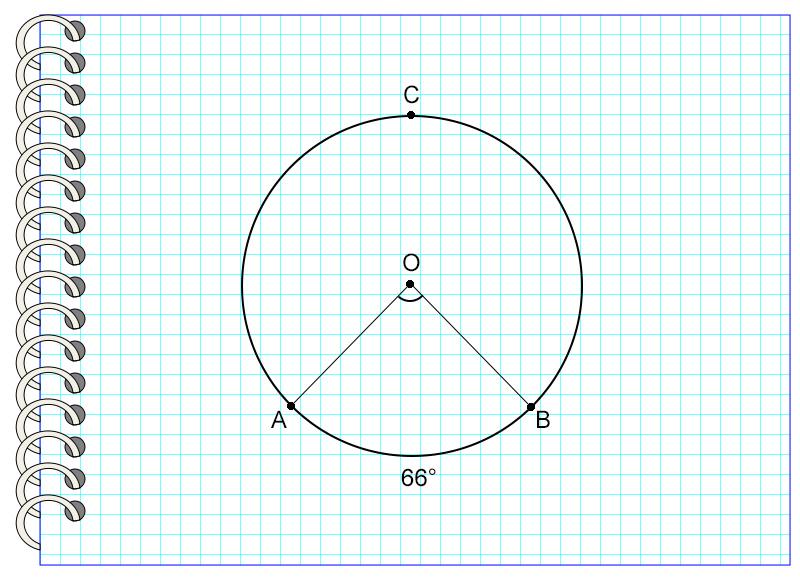
Итак, центральный угол равен градусной мере дуги, на которую он опирается.

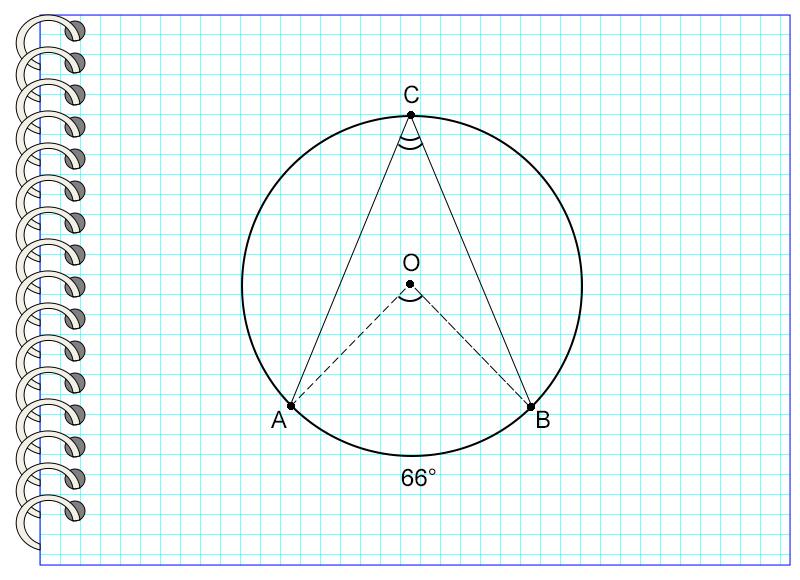
На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.

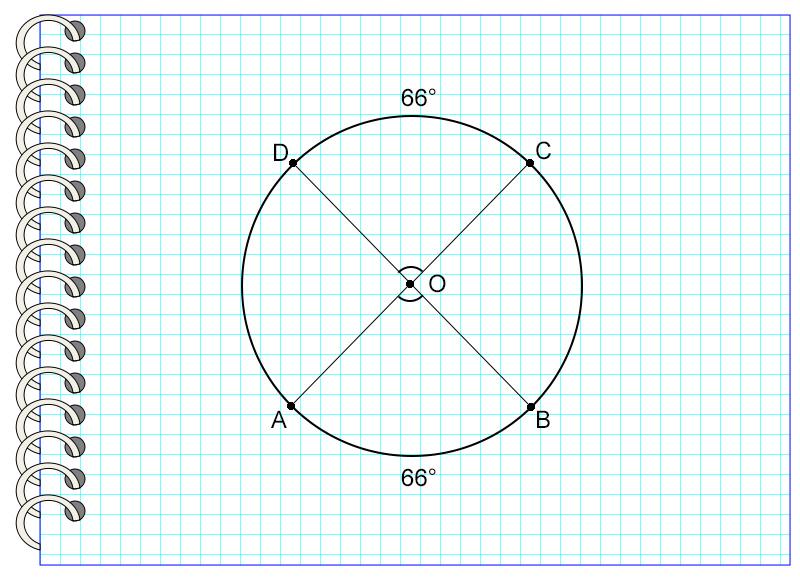
Таким образом, центральные углы, опирающиеся на равные дуги, равны.

На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.

Как найти вписанный угол

Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?

Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.

Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.

Значит, угол АСВ = 66° : 2 = 33°

Рассмотрим некоторые следствия из этой теоремы.

• Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
• Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
• Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
• Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.

Где могут встретиться задачи на эту тему? Их виды и способы решения

Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.

Углы, опирающиеся на одну дугу

Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.

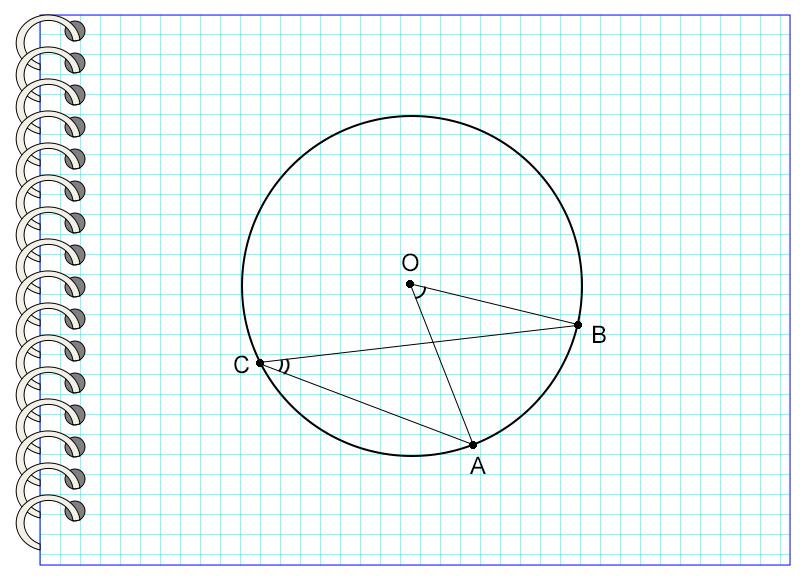
Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.

Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла — общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,

1) АОВ = 54° : 2 = 27°.

Углы, опирающиеся на разные дуги одной окружности

Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.

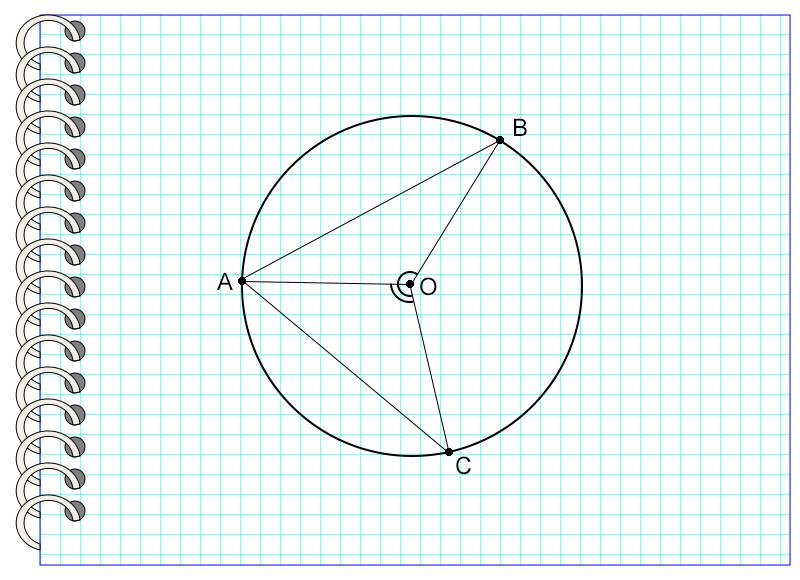
В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.

Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий. Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.

Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.

Точно так же угол АОВ опирается на дугу АВ.

Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.

ВС = 360° — АС — АВ

ВС = 360° — 120° — 30° = 210°

Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.

Угол САВ = 210° : 2 = 110°

Задачи, основанные на соотношении дуг

Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.

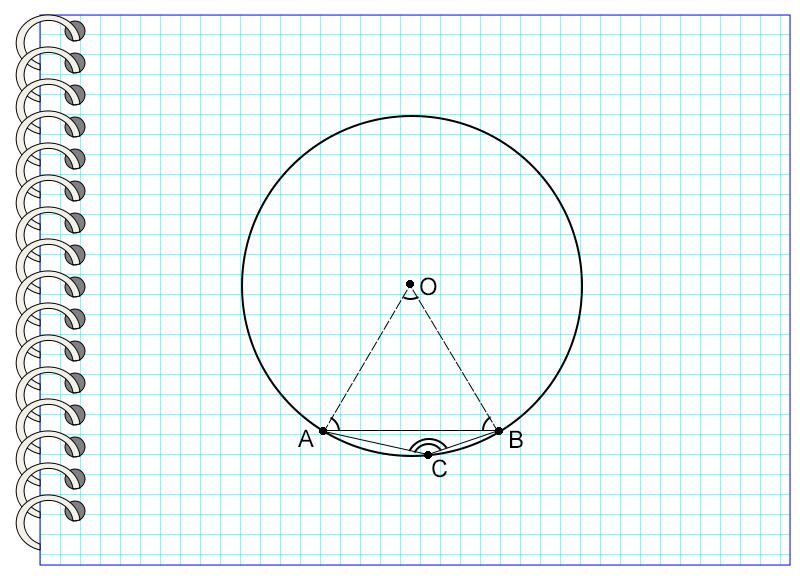
Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.

Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник. Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.

АВ = 360° — 60° = 300°

Угол АВС = 300° : 2 = 150°

В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.

Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.

По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.

Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°

В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги — 50. Вычислите длину большей дуги.

Для того чтобы вычислить длину большей дуги, нужно составить пропорцию — как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.

Большая дуга равна 360° — 60° = 300°.

Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.

Большая дуга = 50 * 5 = 250

Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.

Деление окружности на градусы

Во всем мире принято странное деление окружности на 360 градусов. Со всех точек зрения было бы логичнее деление окружности на 2, потом на 4, потом на 8, 16, 32, 64 и т. д. части. А то поди ж ты: сначала делим окружность на 4 части, потом каждую четверть на 90 градусов. Почему на 90? Почему не на 100 или 120? Оказывается, деление окружности на 360 градусов ведет свое начало от вавилонских жрецов. Они, наблюдая за движением Солнца, обнаружили, что в день равноденствия Солнце от восхода до заката описывает на небесном своде полуокружность, в которой видимый поперечник Солнца укладывается ровно 180 раз. Поэтому-то они и стали каждую полуокружность делить на 180 частей, а каждую окружность – на 360 градусов! Школьный транспортир напоминает, что каждое его деление есть не что иное, как отпечаток – след Солнца, проходящего по небосклону в день равноденствия.

Существует, правда, египетская гипотеза происхождения деления окружности. Длительность года у египтян составляла 360 дней. Год был разбит на 12 месяцев, а каждый месяц на 30 дней. И Солнце по небу проходило каждый год через 12 зодиакальных созвездий. Так что Солнце находилось в каждом из этих созвездий по 30 дней. Итак, за 1 день солнце проходит по небу расстояние в 1 единицу пути. Таких единиц всего 360. И только потом эту единицу пути назвали градусом.

Герой романа Жюля Верна «Таинственный остров» инженер Сайрес Смит, чтобы определить величину острого угла, образованного ножками самодельного циркуля, «измерил этот угол по окружности, разделённой на триста шестьдесят равных частей; угол равнялся десяти градусам». Зачем для измерения острого угла потребовалось делить на части всю окружность, когда достаточно рассмотреть её четверть, непонятно, и как удалось добиться их равенства? Поэтому, деление окружности непростой вопрос, которому во многих задачах стоит уделить время.

Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.

Содержание

Градус [ править | править код ]

Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.

Причина выбора градуса как единицы измерения углов неизвестна. Одна из теорий предполагает, что это связано с тем, что 360 — приблизительное количество дней в году [1] . Некоторые древние календари, такие как древнеперсидский, использовали год в 360 дней.

Другая теория гласит, что аккадцы (вавилоняне) поделили окружность, используя угол равностороннего треугольника как базу и поделив результат на 60, следуя своей шестидесятеричной системе счисления [2] [3] .

Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.

Градус в альтернативных единицах измерения:

1 ∘ = 2 π 360 = >>> радиан = π 180 = 1 p ≈ 1 57,295 779513 ∘ >>= >approx 295779513^ >>>> [4] ≈ 0,017 4532925 0174532925> (радиан в 1°) 1 ∘ = 1 360 = >> оборота=0,002(7) оборота=0,002777777777… 1 ∘ = 400 360 = >> градов=1,(1) градов=1,11111111111… градов

Минуты и секунды [ править | править код ]

По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″. Ранее употреблялась величина в 1/60 секунды — терция (третье деление), с обозначением тремя штрихами — z″′. Деление градуса на минуты и секунды ввёл Клавдий Птолемей [5] ; корни же такого деления восходят к учёным Древнего Вавилона (где использовалась шестидесятеричная система счисления).

Минуты и секунды в других системах измерения:

1 ′ = 2 π 360 ∘ ⋅ 60 ′ = 1 ′ p ′ ≈ 1 ′ 3437,747 ′ >cdot 60′>>= 747′>>> [4] ≈ 2,908 88208 ⋅ 10 − 4 rad 90888208cdot 10^

>> (1 минута в радианах) 1 ″ = 2 π 360 ∘ ⋅ 60 ′ ⋅ 60 ″ = 1 ″ p ″ ≈ 1 ″ 206264 , 8 ″ >cdot 60’cdot 60”>>= >approx 8”>>> [4] ≈ 4,848 136811 ⋅ 10 − 6 rad 848136811cdot 10^

>> (1 секунда в радианах).

Минуты и секунды в радианной мере из-за своих чрезмерно малых величин представляют ограниченный интерес и практически очень мало используются.
Гораздо больший интерес представляет перевод десятичных (сотых, десятитысячных) долей градуса в минуты и секунды и обратно — см. Радиан#Связь радиана с другими единицами и Географические координаты.

Угловая секунда [ править | править код ]

Углова́я секу́нда (англ. arcsecond , arc second , as , second of arc ; синонимы: дуговая секунда, секунда дуги [6] ) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла [7] .

Использование [ править | править код ]

Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается s ). Соотношение между этими величинами определяется формулой 1 s =15″. [8]

Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой [6] [9] , что является простой транслитерацией с англ. arcsecond .

Дольные единицы [ править | править код ]

По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds , mas ), микросекунды (англ. microarcseconds , µas ) и пикосекунды (англ. picoarcseconds , pas ). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению [7] . Однако согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками [10] , в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами ( mas , µas и pas соответственно).

Связь различных угловых единиц измерения

Единица	Величина	Обозначение	Аббревиатура	Радиан (прибл.)
градус	1/360 окружности	°	deg	17,4532925 mrad
минута	1/60 градуса	′	arcmin, amin, ′ ^ >> , MOA	290,8882087 µrad
секунда	1/60 минуты	″	arcsec	4,8481368 µrad
миллисекунда	1/1000 секунды	mas	4,8481368 nrad
микросекунда	1 × 10 −6 секунды	μas	4,8481368 prad

Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.

Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника. [ источник не указан 2692 дня ]

В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP) [11] [12] .

Главная ≫ Инфотека ≫ Математика ≫ По следам вавилонян, или почему в окружности 360 градусов? // Наталья Карпушина

Знаете ли вы, почему в окружности 360 градусов, а не 180 или, скажем, не 300? Откуда пошла традиция делить окружность на равные части и почему было выбрано именно такое их число? Оказывается, этому делению мы обязаны вавилонянам. Согласно их календарю, продолжительность года составляла 360 дней — именно столько раз, по наблюдениям древних астрономов, солнечный диск укладывался на годичном пути светила. Иными словами, за каждые сутки солнце делало один «шаг». Поэтому вавилоняне и разделили окружность на 360 равных частей, каждую из которых называют градусом (от лат. gradus — шаг, ступень). Считается, что они же изобрели простейший инструмент для измерения углов − транспортир. Но вот вопрос: как же древние сумели разделить окружность на равные части, не владея техникой геометрических построений и располагая лишь примитивными инструментами? Загадка…

С подобной проблемой однажды столкнулся инженер Сайрес Смит, герой романа Жюля Верна «Таинственный остров». Чтобы определить величину острого угла, образованного ножками самодельного циркуля, он «измерил этот угол по окружности, разделённой на триста шестьдесят равных частей; угол равнялся десяти градусам». Вот, собственно, и всё, что сообщает о решении данной задачи Жюль Верн. Непонятно, зачем для измерения острого угла потребовалось делить на части всю окружность, когда достаточно рассмотреть её четверть, и уж совсем неясно, как удалось добиться их равенства. Можно лишь предположить, что инженер выполнял построения на земле с помощью подручных средств, как он не раз поступал при решении других практических задач, если те требовали знания геометрии.

Сначала прикинем решение на бумаге. Для того чтобы разделить окружность на равные части, пригодится диск, край которого представляет собой окружность фиксированной длины l . Если катить диск по нарисованной на земле окружности длиной L = nl , где n = 2, 3, 4 …, то через n оборотов он обежит линию и вернётся в исходную точку. Пришло время проявить смекалку: сделаем на краю диска «острый выступ», оставляющий на земле отметку после каждого оборота. С его помощью мы разметим окружность, то есть разобьём на равные части. Допустим, нужно разделить окружность на дуги по 10°. В таком случае n = 360° : 10° = 36. Так как L превосходит l в 36 раз, то из соображений подобия и радиус R нарисованной на земле окружности должен быть во столько же раз больше радиуса r диска.

Теперь можно переходить к конкретным действиям. Измерим радиус диска. Пусть для определённости r = 5 см, тогда R = 180 см. Сделаем в диске отверстие по линии радиуса и вставим в него, например, кусочек спицы так, чтобы острый конец чуть торчал наружу. Отмерим кусок верёвки длиной 180 см и привяжем к его концам по колышку. Один колышек вобьём в землю, затем натянем верёвку и, удерживая её в таком состоянии, очертим другим колышком окружность. Наконец, прокатим по нарисованной линии диск; 36 меток (следов спицы) разделят окружность на дуги по 10° в каждой. Задача решена. Ясно, что в общем случае, подбирая подходящую длину радиуса R и количество «зарубок» на диске, легко разделить окружность на нужное число равных частей.

Задачу можно решить и по-другому, как делали древние египтяне, строя прямой угол при помощи верёвки, разделённой узелками на равные части. За единицу измерения примем длину диска. Обмотаем верёвку вокруг диска и завяжем на конце отмеренного отрезка узелок. Проделаем ту же операцию необходимое число раз. Затем положим размеченную таким образом верёвку поверх нарисованной на земле окружности (узелки соответствуют меткам, которые оставил бы на земле катящийся диск в первом способе построения). В данном случае при вычерчивании окружности можно обойтись без рулетки: радиус R окружности получим, отложив на верёвке диаметр диска n /2 раз (при нечётном n придётся добавить длину радиуса).

Проигрывая в точности построений, мы вместе с тем выигрываем в их простоте и доступности, что на практике зачастую ценится больше. Добавим, что верёвка с узелками — это примитивный циркуль, который используется до сих пор, когда надо провести на земле дугу большого радиуса, например при разметке спортивной арены, или очертить круг при разбивке клумбы.

💡 Видео

Комментарии: 0