Какое из следующих утверждений верно?
1) В треугольнике против большего угла лежит большая сторона.
2) Диагонали ромба равны.
3) Площадь параллелограмма равна половине произведения его диагоналей.
В ответ запишите номер выбранного утверждения.
1) В треугольнике против бо́льшего угла лежит бо́льшая сторона — верно.
2) Диагонали ромба равны — неверно.
3) Площадь параллелограмма равна половине произведения его диагоналей — неверно.
Теорема о соотношениях между углами и сторонами треугольника
Теорема о соотношениях между углами и сторонами
треугольника звучит так:
В треугольнике напротив большего угла лежит
большая сторона, и обратно, напротив большей
стороны лежит больший угол.
Доказательство теоремы
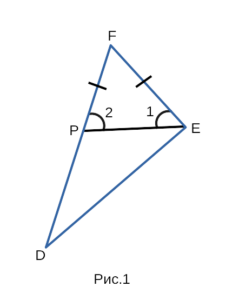
Эту теорему мы докажем, используя рисунок 1, где изображен
треугольник DFE.
1. Предположим, что в треугольнике DFE сторона FE ∠D.
Отложим на стороне DF отрезок FP = FE. В результате ∠1 = ∠2,
а сторона PF = FE, следовательно треугольник PFE — равнобедренный.
∠1 является частью ∠E, значит ∠1 ∠D. Так, как ∠1 и ∠2 равны, а ∠1
является частью ∠E, ∠2 > ∠D, значит ∠E > ∠D.
2. Допустим, что в треугольнике DFE ∠E > ∠D. Докажем,
что сторона FD > FE.
Предположим, что это не так. Тогда сторона FD = FE, или сторона FD ∠E — напротив большей стороны лежит больший угол.
Утверждение в первом и втором случае противоречит условию: ∠E > ∠D. Из этого
следует то, что наше предположение неверно, и, следовательно DF > FE, ∠E >∠D, ч.т.д.
Теорема доказана.
Следствия из доказанной теоремы
Из теоремы, которую мы сейчас доказали следует вот что:
- Гипотенуза в прямоугольном треугольнике больше катета,
так как катеты лежат напротив острых углов, а гипотенуза
лежит напротив прямого угла. - Если две стороны или два угла треугольника равны, то
треугольник равнобедренный, действительно, если в
треугольнике два угла равны, значит и стороны
напротив этих углов равны. - В равнобедренном треугольнике при равных сторонах два
угла равны, а третий больший угол лежит
напротив большей стороны.
Свойства сторон и углов треугольника
| Фигура | Рисунок | Формулировка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Большая сторона треугольника |  | Против большей стороны треугольника лежит больший угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньшая сторона треугольника |  | Против меньшей стороны треугольника лежит меньший угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Длины сторон треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Углы треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешний угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема косинусов |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема синусов |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник | ||
| ||
| Большая сторона треугольника | ||
| Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | ||
| Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | ||
| Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | ||
| Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | ||
| ||
| Углы треугольника | ||
| ||
| Внешний угол треугольника | ||
| ||
| Больший угол треугольника | ||
| ||
| Меньший угол треугольника | ||
| ||
| Теорема косинусов | ||
| ||
| Теорема синусов | ||
| ||
| Треугольник |
|
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.
Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .
Свойство большей стороны треугольника:
Против большей стороны треугольника лежит больший угол
Свойство большего угла треугольника:
Против большего угла треугольника лежит большая сторона
Свойство меньшей стороны треугольника:
Против меньшей стороны треугольника лежит меньший угол
Свойство меньшего угла треугольника:
Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.
a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.
Свойство углов треугольника:
Сумма углов треугольника равна 180°
Свойство внешнего угла треугольника:
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Свойство большего угла треугольника:
Величина большего угла треугольника не может быть меньшей, чем 60°.
,
где α – больший угол треугольника.
Свойство меньшего угла треугольника:
Величина меньшего угла треугольника не может быть большей, чем 60°.
,
где β – меньший угол треугольника.
Свойство меньшего угла треугольника:
,