Углы в пифагоровом треугольнике

В математике есть определенные каноны, которые явились, так сказать, фундаментом или основанием всего последующего развития современной математики. Одним из этих канонов, по праву можно считать теорему Пифагора.

Кому еще со школьных времен не известна смешная формулировка теоремы Пифагора: «Пифагоровы штаны во все стороны равны». Ну да, правильно это звучит так: «квадрат гипотенузы равен сумме квадратов катетов «, но про штаны гораздо лучше запоминается.

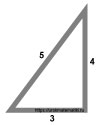
Нагляднее всего это видно на треугольнике со сторонами 3-4-5. Но если изучить внимательно использование такого треугольника в древней истории, то можно заметить одну занимательную вещь и называется она ни как по другому, как Египетский треугольник.

Этот самый философ и математик Пифагор Самосский из Греции, именем которого и названа эта теорема, жил примерно 2,5 тысяч лет тому назад. Ну конечно дошедшая до нашего времени биография Пифагора не совсем достоверна, но, тем не менее, известно что Пифагор много путешествовал по странам Востока. В том числе он был и Египте и Вавилоне. В Южной Италии Пифагор основал свою знаменитую «Пифагорову школу», которая сыграла очень даже важную роль, как в научной, так и политической жизни древней Греции. С тех времен по преданиям Плутарха, Прокла и других известных математиков того времени, считалось, что эта теорема до Пифагора известна не была и именно по этому её назвали его именем.

Но история говорит что это не так. Обратимся туда, где бывал Пифагор и что видел, прежде чем сформулировать свою теорему. Африка, Египет. Бесконечный и однообразный океан песка, почти ни какой растительности. Редкие кустики растений, едва заметные верблюжьи следы. Раскаленная пустыня. Солнце и то кажется тусклым, как будто покрытым этим вездесущим мелким песком.

И вдруг, как мираж, как видение, на горизонте возникают строгие очертания пирамид, изумительных по своим идеальным геометрическим формам, устремленным к палящему солнцу. Своими огромными размерами, и совершенством своих форм они изумляют.

Скорее всего, Пифагор их видел в ином виде, нежели как они выглядят сейчас. Это были сияющие полированные громады с четкими гранями на фоне многоколонных прилегающих храмов. Рядом с величественными царскими пирамидами стояли пирамиды поменьше: жен и родичей фараонов.

Власть фараонов Древнего Египта была непререкаемой. Фараонов считали божеством и отдавали им божественные почести. Фараон-бог был вершителем судьбы народа и его покровителем. Даже после смерти культ фараона имел преогромное значение. Умершего фараона сохраняли веками, и для сохранения тела фараона сооружали гигантские пирамиды. Величие, архитектура и размеры этих пирамид поражают и сейчас. Недаром эти сооружения относили к одному из семи чудес света.

Изначально назначение пирамид было не только как усыпальниц фараонов. Считают что они сооружались как атрибуты могущества, величия, и богатства Египта. Это памятники культуры того времени, хранилища истории страны и сведений о жизни фараона и его народа, собрание предметов быта того времени. Кроме того однозначно, что пирамиды имели определенное «научное содержание». Их ориентирование на местности, их форма, размеры и каждая деталь, каждый элемент настолько тщательно продумывались, что должны были продемонстрировать высокий уровень знаний создателей пирамид. Очевидно что они строились на тысячелетия, «навечно». И недаром арабская пословица гласит: «Все на свете страшится времени, а время страшится пирамид».

Своим аналитическим умом Пифагор не мог не заметить определенную закономерность в формах и геометрических размерах пирамид. Скорее всего, это и натолкнуло Пифагора на анализ этих размеров, что впоследствии и было им выражено своей знаменитой теоремой, от которой ныне и отталкивается современная геометия.

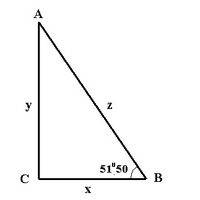
Среди множества пирамид сохранившихся до нашего времени особое место занимает пирамида Хеопса. Если рассмотреть геометрическую модель этой пирамиды и восстановить её первоначальную форму, то очевидно, что её поперечное сечение представляет собой два треугольника с внутренним углом равным 51°50′.

Сейчас пирамида является усеченной, но это разрушения времени, а если геометрически восстановить её в первоначальном виде, то получается что стороны этих треугольников равны: основание СВ = 116, 58 м, высота АС = 148,28 м.

Отношение катетов у/х = 148,28/116,58 = 1,272. А это величина тангеса угла 51град 50 мин. Получается, что в основу треугольника АСВ пирамиды Хеопса было заложено отношение AC/CB = 1,272. Такой прямоугольный треугольник называется «золотым» прямоугольным треугольником.

Получается что основной «геометрической идеей» пирамиды Хеопса является «золотой» прямоугольный треугольник. Но особой в этом отношении является пирамида Хефрена. Угол наклона боковых граней у этой пирамиды равен 53°12, при котором отношение катетов прямоугольного треугольника 4:3. Такой треугольник называют «священным» или «египетским» треугольником. По мнению многих известных историков, «египетскому» треугольнику в древности придавали особый магический смысл. Так Плутарх писал, что египтяне сопоставляли природу Вселенной со «священным» треугольником: символически они уподобляли вертикальный катет мужу, основание — жене, а гипотенузу — тому, что рождается от обоих.

Для египетского треугольника со сторонами 3:4:5 справедливо равенство: 32 + 42 = 52, а это и есть знаменитая теорема Пифагора. По неволе напрашивается вопрос: не это ли соотношение хотели увековечить египетские жрецы, построив пирамиду в основе которой лежит треугольник 3:4:5. Пирамида Хефрена наглядное подтверждение того что знаменитая теорема была известна египтянам задолго до ее открытия Пифагором.

Неизвестно как это попало к древним египтянам, то ли это заслуга их ученых, то ли это дар из вне, не исключается и то, что это дар внеземной цивилизации, но использование такого треугольника давало египетским строителям очень существенную и к тому же простую возможность при возведении таких огромных сооружений соблюдать точные геометрические размеры. Ведь свойства этого треугольника таковы, что его угол между катетами является равный 90 градусов. То есть использование такого элемента позволяет обеспечить точную перпендикулярность сопрягаемых элементов и естественно всей конструкции, что и подтверждает архитектура древнего Египта.

Получить прямой угол без необходимых инструментов не просто. Но если воспользоваться этим треугольником, оказывается все достаточно просто. Нужно взять обычную веревку, разделить её на 12 равных частей, и из них сложить треугольник, стороны которого будут равны 3, 4 и 5 частям. Угол между сторонами длиной 3 и 4 части оказывается и есть прямой. Вот это и есть Египетский треугольник Пифагора.

Во многих исторических письменах имеются следы, что уникальные свойства «египетского треугольника» были известны и широко использовались за много веков до Пифагора и не только в Египте, но и далеко за его пределами: в Месопотамии, в древнем Китае, в Вавилоне.

Знаменитая древнеегипетская пословица «Делай, как делается», дошедшая до наших дней, наталкивает на мысль что сами египтяне, возводившие эти строительные шедевры, были простыми исполнителями и особыми знаниями не обладали, а все секреты были скрыты от непосвященных. Ведь работами на строительстве руководили жрецы — члены особой привилегированной замкнутой касты. Они были хранителями древних знаний, которые держались в секрете. Но пытливый ум великого мыслителя Пифагора сумел разгадать один их этих секретов.

Умы людей всегда будоражат разнообразные загадки, и это, вероятно, будет всегда. Египетский треугольник, хоть и известен человечеству с незапамятных времён, все-таки одна из не полностью разгаданных тайн.

Ведь, что не говори, а форма египетского треугольника и проста, и в то же время гармонична, по своему он даже красив. И с ним достаточно легко работать. Для этого можно использовать самые простые инструменты — линейку и циркуль. Использую этот незатейливый элемент и его симметричные отображения, можно получить красивые, гармоничные фигуры. Это и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих — возрастающих, по размерам египетских треугольников в соответствии с правилом золотого сечения. Это удивительное богатство гармоничных пропорций.

До сих пор в мире есть много пытливые люди, которые как безумцы изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Скорее всего, усилия их тщетны, но даже в случае с Египетским треугольником, ясно что «простых тайн» на земле еще много.

Видео:№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

Теорема Пифагора

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c 2 − b 2
• b = √c 2 − a 2
• c = √a 2 + b 2

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
• если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
• если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a 2 = c * HB, b 2 = c * AH.
• Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Видео:Египетский треугольник. Пифагоровы тройки.Скачать

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

Пусть катеты a = 6 и b = 8.

По теореме Пифагора c 2 = a 2 + b 2 .

Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

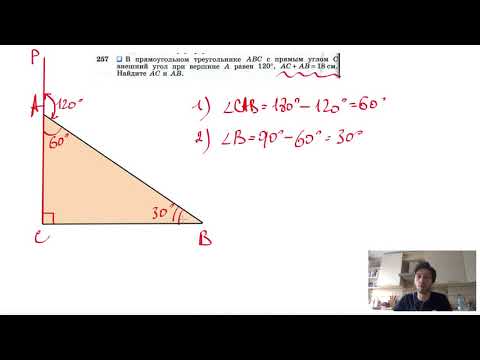
Видео:№257. В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120°Скачать

Теорема Пифагора

Теорема Пифагора — пожалуй, одна из самых известных теорем в математике вообще и геометрии в частности. На самом деле несмотря на то, что она названа именем Пифагора, она была известна еще за тысячу лет до него.

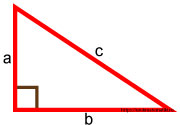
Терема Пифагора гласит следующее: если у нас есть прямоугольный треугольник с катетами a, b и гипотенузой c , то сумма квадратов катетов равна квадрату гипотенузы.

Мы знаем, что величина a 2 описывает площадь квадрата со стороной a . То есть, если мы на катете a построим квадрат, на катете b построим квадрат и на гипотенузе c построим квадрат, мы получим, что площадь квадрата со стороной a + площадь квадрата со стороной b равняется площади квадрата со стороной c . Это, так называемое, геометрическое объяснение теоремы Пифагора: сумма площадей квадратов, построенных на катетах, равняется площади квадрата построенного на гипотенузе.

Если вы построите вместо квадратов любые подобные фигуры, допустим полуокружности, то сумма этих площадей, построенных на катетах, все равно будет равняться площади фигуры, построенной на гипотенузе.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Доказательство теоремы Пифагора

На сегодняшний день известно более 200 различных доказательств теоремы Пифагора. Мы воспользуемся одним из них.

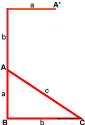
Для того, чтобы доказать теорему Пифагора, мы рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой c .

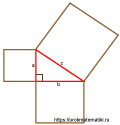
Достроим прямоугольный треугольник со сторонами a, b, c до квадрата следующим образом: катет длиной a мы достраиваем на расстояние b .

Из конца получившегося отрезка a+b проводим перпендикуляр на расстояние a .

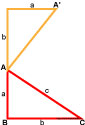
Объединив точки A и A’ , получаем исходный треугольник, только перевёрнутый.

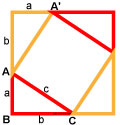
Аналогично достраиваем с других сторон. Получается квадрат со стороной a+b .

• Площадь квадрата со стороной a+b равна квадрату стороны (a+b) .
• Квадрат состоит их четырех одинаковых прямоугольных треугольников и внутренней фигуры — квадрата. Площадь каждого прямоугольного треугольника — половина произведения его катетов.
• Внутренняя фигура — квадрат имеет стороны c .
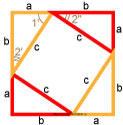
  Докажем, что внутренняя фигура — это квадрат .
  У фигуры все стороны равны — значит это ромб. Если доказать, что один угол является прямым, то все остальные углы будут прямыми.
  Из свойств прямоугольного треугольника мы знаем, что острые углы прямоугольного треугольника равны 90°.
  ∡1′ + ∡2′ = 90°
  Т.к. все показанные треугольники равны, то ∡2′ = ∡2″ и ∡1′ + ∡2″ = 90°
  Отсюда следует, что 180° — ∡1′ + ∡2″ = 90° — это угол между сторонами внутренней фигуры — ромба.
  В нашем случае было доказано, что этот ромб является квадратом.

Преобразовав описанное выше в формулу, получаем:

a + b 2 = 4 · 1 2 a b + c 2

Раскроем формулу квадрата суммы:

a 2 + b 2 + 2 a b = 2 a b + c 2

a 2 + b 2 + 2 a b = 2 a b + c 2

Мы доказали теорему Пифагора.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Задачи на тему «Теорема Пифагора»

Египетский треугольник

Дано:
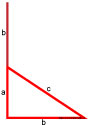
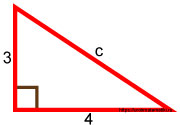
Прямоугольный треугольник с катетами 3 и 4 .

Требуется найти его гипотенузу.

Решение:
Обозначим гипотенузу как c и воспользуемся теоремой Пифагора: сумма квадратов катетов равняется квадрату гипотенузы:
3 2 + 4 2 = c 2
9 + 16 = c 2
25 = c 2
c = 5

Ответ: гипотенуза прямоугольного треугольника с катетами с катетами 3 и 4 равна 5 .

Прямоугольный треугольник со сторонами 3 , 4 и 5 называется египетским.

Пифагорова тройка

Дано:
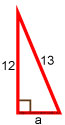
Гипотенуза равна 13 , а один из катетов равен 12 .

Требуется найти второй катет.

Решение:
Обозначим второй катет как a и снова воспользуемся теоремой Пифагора: сумма квадратов катетов равняется квадрату гипотенузы:
12 2 + a 2 = 13 2
144 + a 2 = 169
a 2 = 169 — 144
a 2 = 25
a = 5

Ответ: второй катет a прямоугольного треугольника с гипотенузой 13 и одним из катетов 12 равен 5 .

Обратите внимание, что в первом и втором примерах стороны треугольников получились целыми числами. Такие числа, которые удовлетворяют теореме Пифагора, называются пифагоровыми тройками.

Равнобедренная трапеция

Дано:
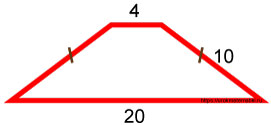
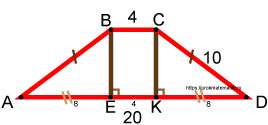
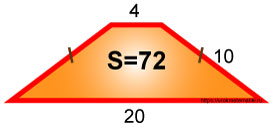
Равнобедренная трапеция. Верхнее основание равно 4 , боковая сторона равна 10 , нижнее основание равно 20 .

Требуется найти площадь трапеции S .

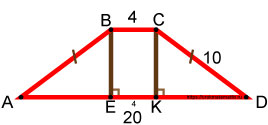
Обозначим углы трапеции точками A, B, C, D . Из точек B и C опустим перпендикуляры на сторону AD в точки E и K соответственно.

Рассмотрим четырёхугольник BCKE . Этот четырёхугольник является прямоугольником. Стороны BC и EK взаимно параллельны, и стороны BE и CK тоже взаимно параллельны, причём один из углов прямоугольника BCKE имеет 90°. Это доказывает, что прямоугольник BCKE является прямоугольником.

В прямоугольнике противоположные стороны равны. Если отрезок BC равен 4 , то EK тоже равен 4 .

Так как наша трапеция равнобокая, то левый и правый треугольники равны между собой, т.к. имеют одинаковые катеты и одинаковые гипотенузы. По признакам равенства прямоугольных треугольников они равны. Это означает, что отрезки AE и KD равны между собой.

Отрезок AD равен 20, отрезок EK равен 4 . Значит, на отрезки ( AE + KD ) остаётся 20 — 4 = 16 . Значит, каждый из них равен 8 .

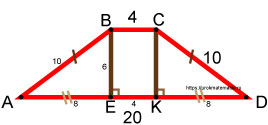
Рассмотрим любой из треугольников, например, ABE . Он является прямоугольным. Один из катетов равен 8 , а гипотенуза равна 10 .

По теореме Пифагора можем найти BE . Сумма квадратов катетов равна квадрату гипотенузы:
BE 2 + 8 2 = 10 2
BE 2 + 64 = 100
BE 2 = 100 — 64
BE 2 = 36
BE = 6
Таким образом мы нашли высоту трапеции.

Теперь можно найти площадь трапеции S .
Площадь трапеции равна полусумме оснований умноженной на высоту трапеции.

Ответ: площадь трапеции S равна 72 .

Видео:Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

Применение теоремы Пифагора

Наиболее частое применение теоремы Пифагора можно увидеть в строительстве. В современные дальномеры встраивается функция, косвенно определяющая размеры стороны (треугольника) при измерении двух других сторон.

Рассмотрим два теоретических примера, когда необходимо произвести расчёт конструкции крыши, а в другом примере научимся позиционировать стены дома относительно друг друга под углом 90°.

Расчет стропильной системы крыши

Задача крайне упрощённая для точных расчётов стропильной системы крыши, но достаточно понятная, чтобы донести принципы расчёта по теореме Пифагора.

Дано:
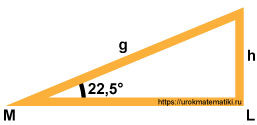
Расстояние между мауэрлатом ( M ) и лежнем ( L ) (они лежат на стенах) известно и равно 5 метрам.
Крыша покрыта металлочерепицей, минимальный рекомендуемый угол наклона которой является 22,5° .
Стойка ( h ) расположена строго перпендикулярно лежню ( L )

Требуется найти длину стропила ( g ) и высоту стойки ( h ).

Чтобы найти высоту стойки ( h ) можно применить теорему синусов. Для этого необходимо найти угол, который лежит против известной стороны. Зная, что сумма углов треугольника равна 180° вычисляем угол, лежащий против известной стороны ML
180° — 90° — 22,5° = 67,5°

Теперь подставляем в формулу известные значения для определения высоты стойки ( h ) по теореме синусов:
sin 22,5° h = sin 67,5° ML

h = 5 · sin 22,5° sin 67,5° = 2.0710678118655

Также по теореме синусов можно найти и длину ( g ), но нас интересует теорема Пифагора.

Поэтому зная, что квадрат гипотенузы (в нашем случае это g ) равен сумме квадратов катетов (в нашем случае это h и расстояние между точками ML ), получаем:

Подставляя в формулу ранее вычисленные и известные значения, получаем:

Ответ: полученные значения исчисляются в метрах. В строительстве округление до миллиметров таких деталей — более чем точно. Поэтому округляя значения стропилы g и стойки h , получаем:

Египетский треугольник

Ещё одним примером практического применения теоремы Пифагора в строительстве может служить использование египетского треугольника.

Чтобы на плоской поверхности вывести угол 90°, необходимо взять верёвку и отложить на ней три расстояния: 3, 4, 5 . И не важно в каких единицах измерения будут отрезки, возможно эти единицы измерения будут выдуманными вами.

Соедините верёвку в треугольник, как показано на изображении, и натяните стороны полученного треугольника.

Угол между сторонами 3, 4 всегда будет равен 90°. По нему можно разметить стены или фундамент будущего дома.

🌟 Видео

Высота в прямоугольном треугольнике. 8 класс.Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

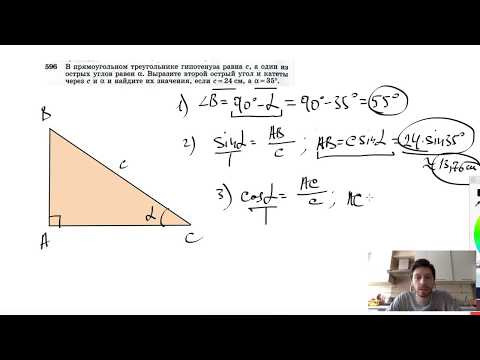
№596. В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен αСкачать

Нахождение косинуса и синуса угла в прямоугольном треугольникеСкачать

Теорема Пифагора для чайников)))Скачать

8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Острые углы прямоугольного треугольника равны 63 и 27. Найдите угол между биссектрисой и медианой...Скачать

Геометрия Найдите острый угол между биссектрисами острых углов прямоугольного треугольникаСкачать