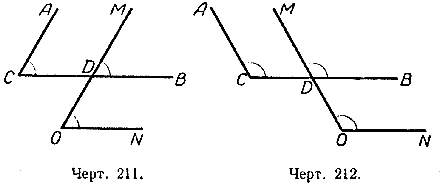Углы с соответственно параллельными или перпендикулярными прямыми

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

1. Углы с соответственно параллельными сторонами.

Возьмём на плоскости две точки С и О и из этих точек проведём две пары лучей СА || ОМ и СВ || ОN так, чтобы углы АСВ и МОN были или оба острые (черт. 211), или оба тупые (черт. 212).

Углы АСВ и МОN — углы с соответственно параллельными cтронами. Докажем, что эти углы равны между собой.

Пусть СВ пересекает ОМ в точке D. ∠АСВ = ∠МDВ, как соответственные углы при параллельных АС и МО и секущей СВ.

∠МDВ = ∠МОN, как соответственные углы при параллельных СВ и ОN и секущей МО, но тогда и ∠АСВ = ∠МОN.

Следовательно, углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.

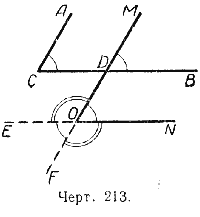
Построим два острых угла АСВ и МОN с соответственно параллельными сторонами (черт. 213): СА || МО и СВ || ОN, и продолжим за вершину О стороны угла МОN.

При вершине О образовались два гупых угла ЕОМ и FОN (так как смежный с ними угол МОN по построению острый).

Каждый из них в сумме с углом МОN составляет 2d, а так как ∠МОN = ∠АСВ, то ∠АСВ+ ∠МОЕ = 2d и ∠АСВ+ ∠FОN = 2d.

Следовательно, углы с соответственно параллельными сторонами в сумме составляют 2d, если один из них острый, а другой тупой.

Видео:Геометрия 7 класс. Углы с соответственно параллельными или перпендикулярнымСкачать

2. Углы с соответственно перпендикулярными сторонами.

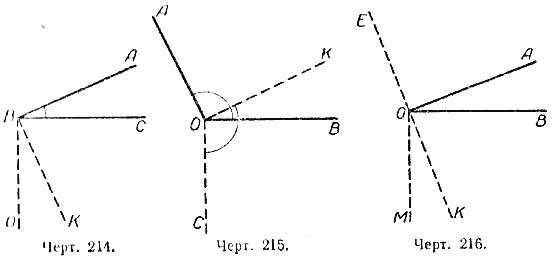
Построим произвольный острый угол АВС. Проведём через вершину угла лучи, перпендикулярные к его сторонам, так, чтобы они образовали острый угол.

BO ВС и ВК ⊥ АВ (черт. 214). Мы получим новый угол OBK. Стороны углов AВС и ОВК взаимно перпендикулярны.

∠АВС = d — ∠СВК; ∠ОВК = d — ∠СВК.

Отсюда следует, что ∠АBС = ∠ОВК.

Построим произвольный тупой угол АОВ и через его вершину проведём лучи, перпендикулярные к его сторонам, так, чтобы они образовали тупой угол.

ОК⊥ОА и ОС⊥ОВ (черт. 215), угол КОС — тупой. Стороны углов АОВ и КОС взаимно перпендикулярны, поэтому

Отсюда следует, что ∠АОВ = ∠КОС.

Углы с соответственно перпендикулярными сторонами равны между собой, если они оба острые или оба тупые.

Построим произвольный острый угол АОВ и проведём через его вершину перпендикуляры к его сторонам так, чтобы они образовали острый угол (черт. 216).

Получим: ∠КОМ = ∠АОВ. Продолжим сторону ОК за вершину О. Стороны угла ЕОМ перпендикулярны сторонам угла АОВ. При этом ∠ЕОМ — тупой, так как смежный с ним ∠МОК — острый. ∠КОМ + ∠ЕОМ = 2d (как углы смежные). Но ∠КОМ по ранее доказанному равен ∠АОВ. Следовательно, и ∠АОВ + ∠ЕОМ = 2d.

Углы с соответственно перпендикулярными сторонами в сумме составляют 2d, если один из них острый, а другой тупой.

Мы рассматривали углы, составленные взаимно перпендикулярными сторонами, когда они имели общую вершину. Выведенные нами свойства будут справедливы и в том случае, когда углы не будут иметь общей вершины.

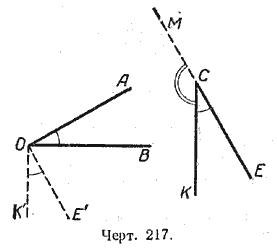
Построим произвольный острый угол АОВ и через какую-нибудь точку С (черт. 217) проведём лучи СЕ⊥ОA и СК⊥ОВ так, чтобы угол КСЕ был тоже острый.

Углы АОВ к КСЕ составлены взаимно перпендикулярными сторонами. Докажем, что они равны между собой. Для этого через точку О (вершину ∠АОВ) проведём ОК&#146||СК и ОЕ&#146 || СЕ. ∠КСЕ = ∠КОЕ&#146, так как они составлены взаимно параллельными сторонами и оба острые. Но ∠К&#146ОЕ&#146 = ∠АОВ по доказанному. Следовательно, ∠АОВ = ∠КСЕ.

Если продолжим сторону СЕ за вершину угла, мы получим ∠МСК, смежный с ∠КСЕ.

∠МСК + ∠КСЕ = 2d, но ∠КСЕ = ∠АОВ, Поэтому ∠АОВ + ∠МСК = 2d.

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Теорема об углах с соответственно перпендикулярными сторонами

Теорема

Дано: АОВ, А₁О₁В₁, ОАО₁А₁, ОВО₁В₁.

Доказать: АОВ = А₁О₁В₁ или АОВ + А₁О₁В₁ = 180 0 .

Доказательство:

1 случай

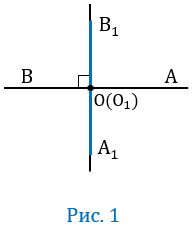
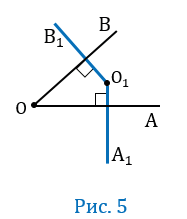
Пусть угол АОВ — развернутый (Рис. 1).

Угол АОВ — развернутый, значит лучи ОА и ОВ будут лежать на одной прямой, при этом по условию ОАО₁А₁, ОВО₁В₁, значит, лучи О₁А₁ и О₁В₁ также будут лежать на одной прямой, следовательно, А₁О₁В₁ — будет развернутым, тогда АОВ = А₁О₁В₁.

2 случай

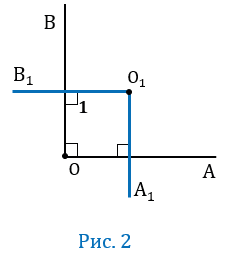
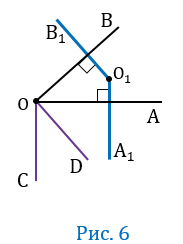
Пусть угол АОВ — прямой, т.е. равен 90 0 (Рис.2).

АОВ = 90 0 , то ОАОВ, при этом по условию ОАО₁А₁, следовательно, ОВО₁А₁. Итак, О₁В₁ — секущая относительно прямых ОВ и О₁А₁, ОВО₁А₁, тогда по теореме об односторонних углах их сумма равна 180 0 , т.е. 1 + А₁О₁В₁ = 180 0 , откуда А₁О₁В₁ = 180 0 —1, при этом по условию ОВО₁В₁, значит 1 — прямой, т.е. 1 = 90 0 , следовательно, А₁О₁В₁ = 180 0 — 90 0 = 90 0 . Из равенств АОВ = 90 0 и А₁О₁В₁ = 90 0 следует, что АОВ = А₁О₁В₁ и АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

3 случай

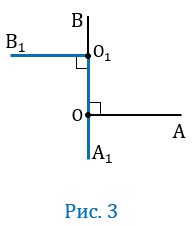
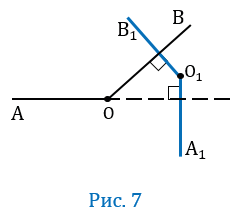
Пусть ОО₁А₁ (Рис.3).

По условию ОО₁А₁, тогда лучи ОВ и О₁А₁ будут лежать на одной прямой А₁В. По условию ОАО₁А₁, ОВО₁В₁, значит, ОА и О₁В₁ будут перпендикулярны одной прямой А₁В, следовательно, ОАО₁В₁. Итак, ОАО₁В₁, А₁В — секущая относительно прямых ОА и О₁В₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90 0 , тогда АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

4 случай

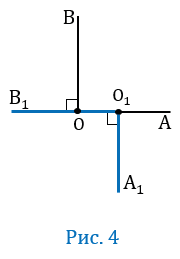
Пусть ОО₁В₁ (Рис.4).

По условию ОО₁В₁, тогда лучи ОА и О₁В₁ будут лежать на одной прямой В₁А. По условию ОАО₁А₁, ОВО₁В₁, значит ОВ и О₁А₁ будут перпендикулярны одной прямой В₁А, следовательно, ОВО₁А₁. Итак, ОВО₁А₁, В₁А — секущая относительно прямых ОВ и О₁А₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90 0 , тогда АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

5 случай

Пусть угол АОВ — острый, т.е. меньше 90 0 , при этом ОО₁А₁, ОО₁В₁ (Рис.5).

Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными (т.е. ОАОС), а точки В и С лежали по разные стороны от прямой ОА. Далее проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными (т.е. ОВОD), а точки С и D лежали по одну сторону от прямой ОА (Рис.6).

Получим, что АОВ = 90 0 — АОD, а СОD = 90 0 — АОD, значит АОВ = СОD. Стороны угла СОD соответственно параллельны сторонам угла А₁О₁В₁, т.е. ОСО₁А₁ (т.к. две прямые перпендикулярные к третьей прямой параллельны друг другу, по построению ОАОС и по условию ОАО₁А₁), также ОDО₁В₁ (т.к. по построению ОВОD и по условию ОВО₁В₁), поэтому по теореме об углах с соответственно параллельными сторонами либо СОD = А₁О₁В₁, либо СОD + А₁О₁В₁ = 180 0 . Следовательно, учитывая то, что АОВ = СОD получим, либо АОВ = А₁О₁В₁, либо АОВ + А₁О₁В₁ = 180 0 .

6 случай

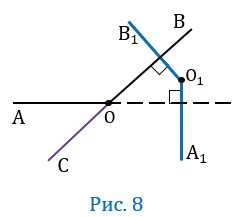
Пусть угол АОВ — тупой, т.е. меньше 180 0 , но больше 90 0 , при этом ОО₁А₁, ОО₁В₁ (Рис.7).

Проведем луч ОС так, чтобы угол АОС был смежным с углом АОВ (Рис.8).

Угол АВС острый, и его стороны соответственно перпендикулярны сторонам угла А₁О₁В₁. Следовательно, либо АОС + А₁О₁В₁ = 180 0 , либо АОС = А₁О₁В₁ (смотри случай 5). Тогда, учитывая, что углы АОС и АОВ смежные, их сумма будет равна 180 0 , значит АОС = 180 0 — АОВ, следовательно, в первом случае 180 0 — АОВ + А₁О₁В₁ = 180 0 , откуда АОВ = А₁О₁В₁, а во втором случае 180 0 — АОВ = А₁О₁В₁, откуда АОВ + А₁О₁В₁ = 180 0 . Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Видео:82 Углы с соответственно перпендикулярными сторонами (150)Скачать

Презентация, геометрия 7 класс по теме: Углы с соответственно параллельными или перпендикулярными сторонами

Видео:П. 30 Углы с соответственно параллельными сторонами - Геометрия 7-9 АтанасянСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Описание слайда:

Углы с соответственно параллельными или перпендикулярными сторонами

Описание слайда:

Теорема:
если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180 градусов

Описание слайда:

Дано: АОВ, А1О1В1, ОАО1А1, ОВО1В1.

Доказать: АОВ = А1О1В1 или АОВ + А1О1В1 = 1800.

Если угол АОВ — развернутый, значит лучи ОА и ОВ будут лежать на одной прямой, при этом по условию ОАО1А1, ОВО1В1, значит точки О1А1 и О1В1 также будут лежать на одной прямой, следовательно, А1О1В1 — будет развернутым, тогда АОВ = А1О1В1 (Рис. 1).

Описание слайда:

Описание слайда:

сли угол АОВ — неразвернутый, то возможны два случая расположения углов АОВ и А1О1В1.
1 случай

Описание слайда:

Описание слайда:

Прямая О1В1 пересекает прямую О1А1 и, следовательно, пересекает параллельную еПй прямую ОА в некоторой точке М (смотри следствие 10 из аксиомы параллельных прямых). Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов (1), образованных при пересечении прямых О1В1 и ОА (Рис.2) равен углу АОВ, т.е. 1 = АОВ (по теореме о накрест лежащих углах). Параллельные прямые ОА и О1А1 пересечены секущей О1М, поэтому 1 = А1О1В1.

Из равенств 1 = АОВ и 1 = А1О1В1 следует, что АОВ =А1О1В1.

Описание слайда:

Описание слайда:

Прямая О1В1 пересекает прямую О1А1 и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М (смотри следствие 10 из аксиомы параллельных прямых). Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов (1), образованных при пересечении прямых О1В1 и ОА (Рис.3) равен углу АОВ, т.е. 1 +А1О1В1 = 1800 (по теореме об односторонних углах). Параллельные прямые ОА и О1А1 пересечены секущей О1М, поэтому 1 = А1О1В1.

Из равенств 1 = АОВ и 1 +А1О1В1 = 1800 следует, что АОВ +А1О1В1 = 1800. Что и требовалось доказать.

Второй случай (рис.3)

Описание слайда:

Теорема:
если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы равны, или в сумме составляют 180 градусов.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 959 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 337 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Презентация к внеклассному мероприятию «Мир в цифрах»

Материалы для учителя в помощь подготовки к ОГЭ-решение задач по геометрии повышенной сложности

Презентация к внеклассному мероприятию «Математическая шкатулка»

Материалы для учителя в помощь подготовки к ОГЭ-решение задач по геометрии повышенной сложности

Презентация по геометрии 8 класс «Ромб»

Зачет № 2 по геометрии «Признаки параллельности прямых»

Контрольная работа по теме :»Тела вращения»

Презентация к уроку геометрии для 7 класса на тему «Признаки параллельных прямых»

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5439521 материал.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Рособрнадзор разрешил провести ВПР по некоторым предметам на компьютерах

Время чтения: 0 минут

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Минпросвещения создает цифровую психологическую службу для школьников

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💡 Видео

ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ 5. Углы с соответственно параллельными и перпендикулярными сторонамиСкачать

Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Тема 18. Углы с соответственно параллельными и соответственно перпендикулярными сторонамиСкачать

Перпендикулярные прямые. 6 класс.Скачать

ЗАДАЧА С УГЛАМИ ИЗ ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #дроби #задачиСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Параллельность прямой и плоскости. 10 класс.Скачать

Углы с сответственно параллельными сторонами 7 классСкачать

Что будет если ВЫПИТЬ КРИТИЧЕСКУЮ ДОЗУ ВОДЫ? | Эксперимент, проверил на себеСкачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Геометрия/7 кл/Углы с соответственно параллельными или перпендикулярными сторонами/11.03.22Скачать

10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Как проверяют учеников перед ЕНТСкачать

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Перпендикулярные прямыеСкачать