Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
- А теперь подробно о тригонометрическом круге:
- Перевод градусов в радианы и обратно: формулы, примеры
- Связь между градусами и радианами
- Формулы перевода радианов в градусы и наоборот
- Примеры перевода градусов в радианы и радианов в градусы
- Синус это х или у в окружности
- Страницы
- среда, 7 ноября 2012 г.
- Тригонометрический круг синус и косинус
- Синус, косинус, тангенс и котангенс. Определения
- Угол поворота
- Числа
- Тригонометрические функции углового и числового аргумента
- Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
- Геометрическое определение синуса и косинуса
- Свойства синуса и косинуса
- Принятые обозначения
- Периодичность
- Четность
- Области определения и значений, экстремумы, возрастание, убывание
- Основные формулы, содержащие синус и косинус
- Сумма квадратов
- Формулы синуса и косинуса суммы и разности
- Формулы произведения синусов и косинусов
- Формулы суммы и разности
- Выражение синуса через косинус
- Выражение косинуса через синус
- Выражение через тангенс
- Таблица синусов и косинусов, тангенсов и котангенсов
- Выражения через комплексные переменные
- Формула Эйлера
- Выражения через гиперболические функции
- Производные
- Интегралы
- Разложения в ряды
- Секанс, косеканс
- Обратные функции
- Арксинус, arcsin
- Арккосинус, arccos
- Тригонометрическое определение
- Табличные значения синуса и косинуса
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Перевод градусов в радианы и обратно: формулы, примеры
Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.
Видео:Тригонометрическая окружность. Как выучить?Скачать

Связь между градусами и радианами
Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.
Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.
Связь градусов с радианами
Связь между радианами и градусами выражается формулой
Видео:Откуда в окружности 2 Пи радиан?Скачать

Формулы перевода радианов в градусы и наоборот
Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.
Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
1 р а д = 180 π ° — градусная мера угла в 1 радиан равна 180 π .
Также можно выразить один градус в радианах.
1 ° = π 180 р а д
Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °
Значит, в одном радиане примерно 57 градусов
1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д
Один градус содержит 0,0175 радиана.
Формула перевода радианов в градусы
x р а д = х · 180 π °
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Видео:Углы, вписанные в окружность. 9 класс.Скачать

Примеры перевода градусов в радианы и радианов в градусы
Пример 1. Перевод из радианов в градусы
Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.
Применим формулу перехода от радианов к градусам и получим:
3 , 2 р а д = 3 , 2 · 180 π ° ≈ 3 , 2 · 180 3 , 14 ° ≈ 576 3 , 14 ° ≈ 183 , 4 °
Аналогично можно получить формулу перевода из градусов в радианы.
Формула перевода из градусов в радианы
y ° = y · π 180 р а д
Переведем 47 градусов в радианы.
Согласно формуле, умножим 47 на пи и разделим на 180.
Видео:Как искать точки на тригонометрической окружности.Скачать

Синус это х или у в окружности
Математика – это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Страницы
Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

среда, 7 ноября 2012 г.
Тригонометрический круг синус и косинус
Тригонометрический круг представляет значения тригонометрических функций синус (sin) и косинус (cos) в виде координат точек единичной окружности при различных значениях угла альфа в градусах и радианах.
Поскольку я сам вечно путаюсь при переводе координат точек окружности в синусы и косинусы, для простоты все значения косинусов (cos) для углов от 0 до 360 градусов (от 0 пи до 2 пи) подчеркнуты зеленой черточкой. Даже при распечатке этого рисунка тригонометрического круга на черно-белом принтере все значения косинуса будут подчеркнуты, а значения синуса будут без подчеркивания. Если вам интересно, то можете посмотреть отдельные тригонометрические круги для синуса и косинуса.
Напротив указанных углов на окружности расположены точки, а в круглых скобках указаны координаты этих точек. Первой записана координата Х (косинус)
Давайте проведем обзорную экскурсию по этому уголку математического зоопарка. Прежде всего, нужно отметить, что здесь присутствует декартова система координат – одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая – вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы – cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы – sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы – на диване перед телевизором по горизонтали.
В этой системе координат нарисована окружность радиусом, равным единице. Центр окружности находится в начале системы координат – там, где в центе рисунка пересекаются оси абсцисс (ось Х) и ординат (ось У).
Из центра окружности проведены тоненькие черточки, которые показывают углы 30, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 градусов. В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.
Линии углов заканчиваются точками на единичной окружности. Возле каждой точки, в круглых скобках, записаны координаты этой точки. Первой записана координата Х, которая соответствует косинусу угла, образовавшего эту точку. Второй записана координата У этой точки, что соответствует значению синуса угла. По картинке довольно легко находить синус и косинус заданного угла и наоборот, по заданному значению синуса или косинуса, можно легко найти значение угла. Главное, не перепутать синус с косинусом.
Обращаю особое внимание на тот факт, что если вы по значению синуса или косинуса ищите угол, обязательно нужно дописывать период угла. Математики очень трепетно относятся к этому аппендициту тригонометрических функций и при его отсутствии могут влепить двойку за, казалось бы, правильный ответ. Что такое период при нахождении угла по значению тригонометрической функции? Это такая штучка, которая придумана математиками специально для того, чтобы запутываться самим и запутывать других. Особенно блондинок. Но об этом мы поговорим как-нибудь в другой раз.
Всё, что собрано в кучку на рисунке тригонометрического круга синуса и косинуса, можно внимательно рассмотреть на отдельных картинках с портретами синуса 0, 30, 45 градусов (ссылки на отдельные странички я буду добавлять по мере увеличения фотогалереи синусов и косинусов).
Синусы и косинусы круг – здесь картинка во всей своей тригонометрической красе.
Угол 120 градусов в радианах – равен 2/3 пи или 2 пи деленное на 3, на картинке очень красиво нарисовано.
Значения синусов косинусов углов в радианах – на картинке есть такие, надеюсь, именно те углы, которые вы ищете.
Значение косинуса угла в 45 градусов – равно корню из двух деленному на два, можете проверить по рисунку.
Тригонометрическая окружность – я не совсем уверен, что представленная на картинке окружность является тригонометрической, но что-то от тригонометрии в этой окружности определенно есть, например, синусы и косинусы на окружности – вылитая тригонометрия.
Тригонометрический круг рисунок – есть здесь такой. Правда, не самый красивый рисунок, можно нарисовать гораздо красивее и понятнее. Мне минус в репутацию – почему я до сих пор не нарисовал его для блондинок? Представляете ситуацию в картинной галерее будущего: экскурсовод объясняет группе школьников «Перед вами всемирно известное полотно «Тригонометрическая мадонна с единичным отрезком на руках» – картина гениального художника эпохи Раннего Математического Возрождения . » Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!
Круг синусов и косинусов – именно такой круг совершенно случайно оказался здесь на картинке.
Угол 9 градусов сколько это в пи – в пи это 1/20 или пи/20.
Решение: для перевода градусов в пи радиан, нужно имеющиеся у нас градусы разделить на 180 градусов (это 1 пи радиан). У нас получается 9/180 = 1/20
Ответ: 9 градусов = 1/20 пи.
Синус это вверх или в сторону – синус – это вверх, в сторону – это косинус.
Комментарии к этой статье запрещены. Из-за огромного их количества мои ответы на ваши вопросы о тригонометрическом круге уже не публикуются. Вопросы можете задавать в комментариях к другим страницам. Постараюсь решить проблему за счет удаления части комментариев, тем самым освобожу место для новых.
Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Видео:Радианная мера угла. 9 класс.Скачать

Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.
Видео:Как запомнить тригонометрический круг специально ничего не выучивая?Скачать

Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Видео:🔴 ЕГЭ-2024 по физике. Движение зарядов в магнитном полеСкачать

Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Видео:Угловая скорость и радианная мера углаСкачать

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Геометрическое определение синуса и косинуса
α – угол, выраженный в радианах.
Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Свойства синуса и косинуса
Видео:Что такое радиан?Скачать

Принятые обозначения
( sin^2 x equiv (sin x)^2; ) ( quad sin^3 x equiv (sin x)^3; ) ( quad sin^n x equiv (sin x)^n ) ( sin^ x equiv arcsin x ) ( (sin x )^ equiv dfrac1 equiv cosec x ) .
( cos^2 x equiv (cos x)^2; ) ( quad cos^3 x equiv (cos x)^3; ) ( quad cos^n x equiv (cos x)^n ) ( cos^ x equiv arccos x ) ( (cos x )^ equiv dfrac1 equiv sec x ) .
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
( sin(x + 2pi) = sin x; quad ) ( cos(x + 2pi) = cos x )
Четность
Функция синус – нечетная. Функция косинус – четная.
( sin( -x ) = – sin x; quad ) ( cos( -x ) = cos x )
Области определения и значений, экстремумы, возрастание, убывание
Основные свойства синуса и косинуса представлены в таблице (n – целое).
| ( small -dfrac 2 + 2pi n ) ( small ( small dfrac 2 + 2pi n ) | ( small -pi + 2pi n ) ( small ( small 2pi n ) | |
| Убывание | ( small dfrac 2 + 2pi n ) ( small ( small dfrac 2 + 2pi n ) | ( small 2pi n ) ( small ( pi + small 2pi n ) |
| Максимумы, ( small x = ) ( small dfrac 2 + 2pi n ) | ( small x = 2pi n ) | |
| Минимумы, ( small x = ) ( small -dfrac 2 + 2pi n ) | ( small x = ) ( small pi + 2pi n ) | |
| Нули, ( small x = pi n ) | ( small x = dfrac 2 + pi n ) | |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Видео:Вписанные углы в окружностиСкачать

Основные формулы, содержащие синус и косинус
Сумма квадратов
( sin^2 x + cos^2 x = 1 )
Формулы синуса и косинуса суммы и разности
( sin(x + y) = sin x cos y + cos x sin y )
( sin(x – y) = sin x cos y – cos x sin y )
( cos(x + y) = cos x cos y – sin x sin y )
( cos(x – y) = cos x cos y + sin x sin y )
( sin( 2x ) = 2 sin x cos x )
( cos( 2x ) = cos^2 x – sin^2 x = ) ( 2 cos^2 x – 1 = 1 – 2 sin^2 x )
( cosleft( dfrac
2 – x
ight) = sin x ) ; ( sinleft( dfrac
2 – x
ight) = cos x )
( cos( x + pi ) = – cos x ) ; ( sin( x + pi ) = – sin x )
Формулы произведения синусов и косинусов
( sin x cos y = ) ( dfrac12 sin( x – y ) + sin( x + y ) )
( sin x sin y = ) ( dfrac12 cos( x – y ) – cos( x + y ) )
( cos x cos y = ) ( dfrac12 cos( x – y ) + cos( x + y ) )
( sin x cos y = dfrac12 sin 2x )
( sin^2 x = dfrac12 1 – cos 2x )
( cos^2 x = dfrac12 1 + cos 2x )
Формулы суммы и разности
( sin x + sin y = 2 , sin dfrac2 , cos dfrac2 )
( sin x – sin y = 2 , sin dfrac2 , cos dfrac2 )
( cos x + cos y = 2 , cos dfrac2 , cos dfrac2 )
( cos x – cos y = 2 , sin dfrac2 , sin dfrac2 )
Выражение синуса через косинус
Далее мы полагаем, что ( n ) – целое число.
Выражение косинуса через синус
Выражение через тангенс
Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
[ img style=»max-w ]
Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Выражения через комплексные переменные
Формула Эйлера
( e^ = cos z + i sin z )
Видео:Выборка с помощью окружностиСкачать

Выражения через гиперболические функции
( sin iz = i sh z ) ( cos iz = ch z )
( sh iz = i sin z ) ( ch iz = cos z )
Производные
( ( sin x )’ = cos x ) ( ( cos x )’ = – sin x ) . Вывод формул > > >
Производные n-го порядка:
( left( sin x
ight)^ = sinleft( x + ndfrac
2
ight) ) ( left( cos x
ight)^ = cosleft( x + ndfrac
Интегралы
( int sin x , dx = – cos x + C ) ( int cos x , dx = sin x + C )
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
Секанс, косеканс
( sec x = dfrac1 ; ) ( cosec x = dfrac1 )
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
( y = arcsin x ) ( left )
( sin( arcsin x ) = x ) ( )
( arcsin( sin x ) = x ) ( left )
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Тригонометрическое определение
С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.
На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.
Рис. 2. Тригонометрическое определение синуса и косинуса
Косинус угла – это абсцисса точки. Синус угла – это ордината точки.
На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки ; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.
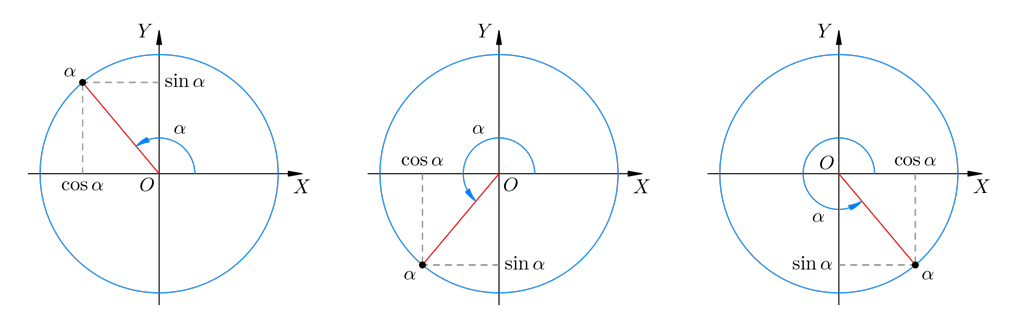
Но теперь мы уже не стеснены первой четвертью и получаем возможность распространить данное определение на любой угол . На рис. 3 показано, что такое синус и косинус угла во второй, третьей и четвёртой четвертях.
Рис. 3. Синус и косинус во II, III и IV четвертях
Табличные значения синуса и косинуса
Абсцисса точки 0 равна 1 , ордината точки 0 равна 0 . Следовательно,