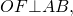Центр вписанной окружности пересечение высот треугольника (4 видео)

Центр вписанной в треугольник окружности

Где лежит центр вписанной в треугольник окружности? Что можно сказать о центре окружности, вписанной в многоугольник?

Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника.

O — точка пересечения биссектрис треугольника ABC.

окр. (O; r) — вписанная.

O — точка пересечения биссектрис ∆ ABC.

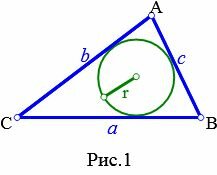
Обозначим точки касания вписанной в треугольник окружности со сторонами AC, BC и AB соответственно M, K. F.

Соединим отрезками центр окружности с точками A, M и F.

(как радиусы, проведенные в точки касания). Следовательно, треугольники AOF и AOM — прямоугольные.

У них общая гипотенуза AO, катеты OF=OM (как радиусы).

Следовательно, треугольники AOF и AOM равны (по катету и гипотенузе).

Из равенства треугольников следует равенство соответствующих углов: ∠OAF=∠OAM.

Значит, точка O лежит на биссектрисе треугольника, проведенной из вершины A.

Аналогично из равенства треугольников BOF и BOK, COM и COK доказывается, что точка O лежит на биссектрисах треугольника ABC, проведенных из вершин B и C.

Следовательно, центр вписанной в треугольник окружности лежит в точке пересечении биссектрис этого треугольника.

Что и требовалось доказать.

Доказательство теоремы можно основать непосредственно на свойстве биссектрисы угла.

1) OM=OF=OK (как радиусы),

2) OM⊥AC, OM⊥AB, OK⊥BC (как радиусы, проведённые в точку касания).

Значит точка O равноудалена от сторон углов BAC, ABC и ACB.

Так как любая точка, лежащая внутри неразвёрнутого угла и равноудалённая от сторон этого угла, лежит на его биссектрисе, то AO, BO и CO — биссектрисы треугольника ABC, O — точка их пересечения.

Аналогично, центр вписанной в многоугольник окружности (если в него можно вписать окружность) лежит в точке пересечения биссектрис этого многоугольника.

Содержание

Свойства высот треугольника. Ортоцентр
Окружность, вписанная в треугольник
Определение окружности, вписанной в треугольник
Теорема об окружности, вписанной в треугольник
🎦 Видео

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Свойства высот треугольника. Ортоцентр

Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК

Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.

1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если , и , если

Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
Четырехугольник ВКМН также можно вписать в окружность.
Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
,где R – радиус описанной окружности .

Докажем эти факты по порядку.

1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам

Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.

2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .

Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.

3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН — прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.

4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,

Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.

5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, .

Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что

Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)

2. В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и

а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .

— смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).

Видео:Задание 16 ЕГЭ по математикеСкачать

Окружность, вписанная в треугольник

Видео:Диагностическая работа-1 в формате ОГЭ. Задача-25Скачать

Определение окружности, вписанной в треугольник

Определение 1. Окружностью, вписанной в треугольник называется окружность, которая находится внутри треугольника и касается всех его сторон (Рис.1).

Центр вписанной окружности пересечение высот треугольника

Можно дать и другое определение окружности, вписанной в треугольник.

Определение 2. Окружностью, вписанной в треугольник называется наибольшая окружность, которая может находится внутри треугольника.

При этом треугольник называется треугольником описанным около окружности . Центр вписанной в треугольник окружности явлется точка пересечения биссектрис треугольника. Центр окружности вписанной в треугольник называется инцентром треугольника.

Видео:Геометрия 8 класс (Урок№31 - Теорема о пересечении высот треугольника.)Скачать

Теорема об окружности, вписанной в треугольник

Теорема 1. В любой треугольник можно вписать окружность.

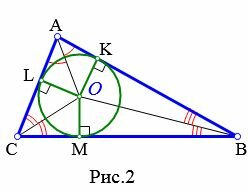Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения биссектрис треугольника. Проведем из точки O перпендикуляры OK, OL и OM к сторонам AB, AC, BC, соответственно. Поскольку точка O равноудалена от сторон треугольника ABC, то OK=OL=OM. Тогда окружность с центром O и радиусом OK проходит через три точки K, L, M. Стороны AB, AC, BC треугольника ABC касаются этой окружности в точках K, L, M, поскольку они перпендикулярны к радиусам OK, OL, OM, соответственно. Следовательно, окружность с центром O и радиусом OK является вписанной в треугольник ABC.

Замечание 1. В любой треугольник можно вписать только одну окружность.

Доказательство. Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой из этих окружностей равноудален от сторон треугольника и совпадает с точкой O пересечения биссектрис треугольника. Радиус этих окружностей равен расстоянию от точки O до сторон треугольника. Поэтому эти окружности совпадают.