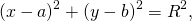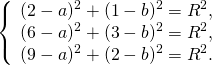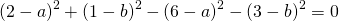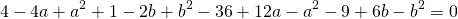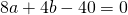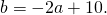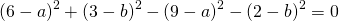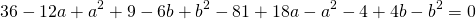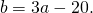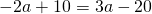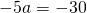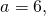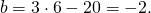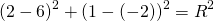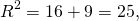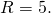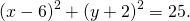Центр описанной окружности в треугольнике по координатам его вершин

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Найти координаты центра описанной окружности по координатам

Видео:Построить описанную окружность (Задача 1)Скачать

Уравнение описанной окружности

Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?

Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.

Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).

Подставив координаты вершин треугольника в уравнение окружности

получим систему уравнений

Вычтем из первого уравнения системы второе:

Теперь из второго уравнения системы вычтем третье:

Приравняем правые части равенств b=-2a+10 и b=3a-20:

Подставим в первое уравнение системы a=6 и b=-2:

a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности

Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Центр описанной окружности треугольника

Если треугольник вписан в окружность так, что его вершины располагаются на окружности, такая окружность называется описанной, а треугольник считается вписанным в данную окружность.

Центр окружности расположен в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника. Серединный перпендикуляр — прямая, которая проходит через середину отрезка, перпендикулярно ему.
Вокруг треугольника возможно описать только одну окружность.

Чтобы определить радиус R описанной окружности, необходимо произведение сторон треугольника (a × b × с) разделить на учетверенную S — площадь треугольника:
R = (a × b × с) / 4S.

Если окружность описана около равностороннего треугольника, радиус R равняется:
R = a /√3.

В том случае, когда окружность описана около прямоугольного треугольника, середина его гипотенузы (с ) является центром описанной окружности.
Радиус R составляет ½ гипотенузы: R = с/2.

Радиус окружности R также равняется медиане m, проведенной к гипотенузе: R = m.

Воспользовавшись онлайн калькулятором, вы сможете быстро и правильно определить координаты центра описанной окружности.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Уравнение окружности по трем точкам

Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.

Уравнение окружности

r 2 = (x — h) 2 + (y — k) 2

• h,k — координаты центра Окружности
• x,y — координаты точки окружности
• r — радиус

Пример

Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)

Решение :

Подставляем координаты точек в формулу

1. (2 — h) 2 + (2 — k) 2 = r 2
2. (2 — h) 2 + (4 — k) 2 = r 2
3. (5 — h) 2 + (5 — k) 2 = r 2

Шаг :2

Найдем значение k упрощая 1 и 2 уравнения

• (2 — h) 2 + (2 — k) 2 = (2 — h) 2 + (4 — k) 2
• 4 — 4h + h 2 + 4 — 4k + k 2 = 4 — 4h + h 2 +16 — 8k + k 2
• 8 — 4k = 20 — 8k
• k= 3

Шаг :3

Найдем значение h упрощая уравнения 2 и 3

• (2 — h) 2 + (2 — k) 2 = (5 — h) 2 + (5 — k) 2
• 4 — 4h + h 2 + 4 — 4k + k 2 = 25 — 10h + h 2 + 25 — 10k + k 2
• 8 — 4k — 4h = 50 — 10h — 10k
• 6k + 6h = 42

Подставив значение k=3 в уравнение

Получаем координаты точки центра (h,k) = ( 4,3 )

Шаг :4

Подставим значения h,k в формулу

• r 2 = (x — h) 2 + (y — k) 2
• r 2 = (2 — 4) 2 + (2 — 3) 2
• r 2 = (-2) 2 + (-1) 2
• r 2 = 5
• r = 2.24

Шаг :5

Подставим значения h, k в уравнение окружности

(x — h) 2 + (y — k) 2

Уравнение окружности = (x — 4) 2 + (y — 3) 2

💥 Видео

Уравнение окружности описанной около треугольникаСкачать

Задание 3 ЕГЭ по математике. Урок 73Скачать

Радиус описанной окружностиСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Задание 3 №27699 ЕГЭ по математикеСкачать

Найти центр и радиус окружностиСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать