Центр описанной около четырехугольника окружности всегда лежит внутри (5 видео)

Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Около любого треугольника можно описать окружность.

Содержание

Доказательство
Доказательство
Доказательство
Доказательство
Доказательство
Центр описанной около четырехугольника окружности всегда лежит внутри
Решение №2182 Какое из следующих утверждений верно? 1) Сумма углов выпуклого четырёхугольника равна 360 градусам.
📺 Видео

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Около треугольника можно описать только одну окружность.

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Около четырехугольника не всегда можно описать окружность.

Доказательство

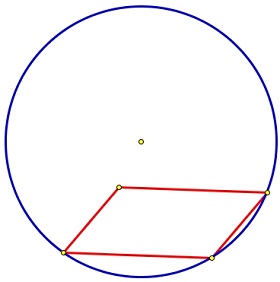
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 .

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность.

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Центр описанной около четырехугольника окружности всегда лежит внутри

Какое из следующих утверждений верно?

1. Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

2. Сумма углов равнобедренного треугольника равна 180 градусам.

3. Диагонали ромба равны.

В ответ запишите номер выбранного утверждения.

Рассмотрим каждое из утверждений:

1. Центр описанной около треугольника окружности всегда лежит внутри этого треугольника — неверно

2. Сумма углов равнобедренного треугольника равна 180 градусам — верно для любого треугольника.

3. Диагонали ромба равны — неверно, диагонали у ромба равны только в частном случае ромба — квадрате.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Решение №2182 Какое из следующих утверждений верно? 1) Сумма углов выпуклого четырёхугольника равна 360 градусам.

Какое из следующих утверждений верно?

1) Сумма углов выпуклого четырёхугольника равна 360 градусам.
2) Средняя линия трапеции равна сумме её оснований.
3) Любой параллелограмм можно вписать в окружность.

В ответ запишите номер выбранного утверждении.

Источник: ОГЭ Ященко 2022 (36 вар)

1) верно , по теореме о сумме углов выпуклого многоугольника, сумма углов n-угольника равна 180°(n − 2):

180°(n − 2) = 180°(4 − 2) = 180°·2 = 360°

2) не верно , средняя линия трапеции равна полусумме её оснований;
3) не верно , ниже пример параллелограмма который нельзя вписать в окружность: