Вписанный угол окружности — это угол, образованный двумя хордами, исходящими из одной точки, то есть вписанным углом называется угол, вершина которого лежит на окружности.
Угол ABC — вписанный угол. ∠ABC опирается на дугу AC, заключённую между его сторонами.
Видео:2020 точка О центр окружности на которой лежат точки A B и C известно что Угол ABC равен 62 градусаСкачать

Теорема о вписанном угле
Теорема:
Вписанный угол измеряется половиной дуги, на которую он опирается.
Это следует понимать так: вписанный угол содержит в два раза меньше градусов, чем дуга, на которую он опирается:
| ∠ABC = | 1 |  AC. AC. |
| 2 |
При доказательстве этой теоремы следует рассмотреть три возможных случая расположения вписанного угла относительно центра окружности.
Первый случай. Сторона вписанного угла проходит через центр окружности.
Соединим точку A с центром круга (точкой O). Получим равнобедренный треугольник AOB, в котором AO = OB, как радиусы одной окружности. Следовательно, ∠A = ∠B, как углы при основании равнобедренного треугольника.
Так как ∠AOC — внешний угол равнобедренного треугольника, то:
а так как углы A и B равны, то
| ∠B = | 1 | ∠AOC. |
| 2 |
Но ∠AOC — центральный угол, значит ∠AOC = 
| ∠ABC = ∠B = | 1 |  AC. AC. |
| 2 |
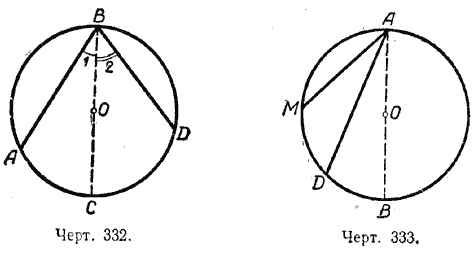
Второй случай. Центр окружности лежит между сторонами вписанного угла.
Проведём диаметр BD. Угол ABC разбился на два угла: ∠1 и ∠2.
Точка D разделяет дугу AC на две дуги: 

| ∠1 = | 1 |  AD и ∠2 = AD и ∠2 = | 1 |  DC. DC. |
| 2 | 2 |
Следовательно, весь угол ABC будет измеряться половиной дуги AC:
| ∠1 + ∠2 = | 1 |  AD + AD + | 1 |  DC DC |
| 2 | 2 |
| ∠ABC = | 1 |  AC. AC. |
| 2 |
Третий случай. Центр окружности лежит вне вписанного угла.
Проведём диаметр BD.
Но ∠ABD измеряется половиной дуги AD , а ∠CBD измеряется половиной дуги CD. Следовательно,
| ∠ABC = | 1 | ( AD — AD —  CD), CD), |
| 2 |
| ∠ABC = | 1 |  AC. AC. |
| 2 |
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Следствия из теоремы
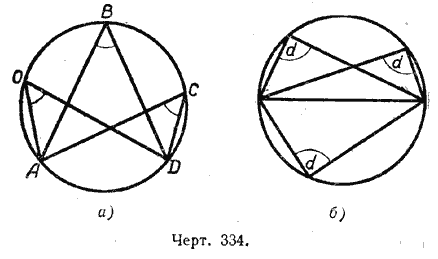
1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги.
2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности.
Половина окружности содержит 180°, значит, угол, опирающийся на диаметр, содержит 90°.
Видео:Геометрия Докажите что если вершина угла лежит вне окружности а угол опирается на диаметр окружностиСкачать

Углы, связанные с окружностью
 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
Видео:Диагностическая работа-1 в формате ОГЭ. Задача-25Скачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Углы с вершинами внутри и вне кругаСкачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать  Центр окружности лежит вне углаОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР. § 76. ВПИСАННЫЕ И НЕКОТОРЫЕ ДРУГИЕ УГЛЫ. 1. Вписанный угол. Угол, вершина которого находится на окружности, а стороны являются хордами, называется вписанным. Угол АВС — вписанный угол. Он опирается на дугу АС, заключённую между его сторонами (черт. 330). Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Это надо понимать так: вписанный угол содержит столько угловых градусов, минут и секунд, сколько дуговых градусов, минут и секунд содержится в половине дуги, на которую он опирается. При доказательстве этой теоремы надо рассмотреть три случая. Первый случай. Центр круга лежит на стороне вписанного угла (черт. 331). Пусть / АВС — вписанный угол и центр круга О лежит на стороне ВС. Требуется доказать, что он измеряется половиной дуги АС. Соединим точку А с центром круга. Получим равнобедренный / AОВ, в котором Но / АОС измеряется дугой АС, следовательно, / В измеряется половиной дуги АС. Например, если Второй случай. Центр круга лежит между сторонами вписанного угла (черт. 332). Пусть / АВD — вписанный угол. Центр круга О лежит между его сторонами. Требуется доказать, что / АВD измеряется половиной дуги АD. Для доказательства проведём диаметр ВС. Угол АВD разбился на два угла: / 1 и / 2. / 1 измеряется половиной дуги АС, а / 2 измеряется половиной дуги СD, следовательно, весь / АВD измеряется 1 /2 Третий случай. Центр круга лежит вне вписанного угла (черт. 333). Пусть / МАD — вписанный угол. Центр круга О находится вне угла. Требуется доказать, что / МАD измеряется половиной дуги МD. Для доказательства проведём диаметр АВ. / МАD = / МАВ— / DАВ. Но / МАВ измеряется 1 /2 Следствия. 1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги (черт. 334, а). 2. Вписанный угол, опирающийся на диаметр,—прямой, так как он опирается на половину окружности. Половина окружности содержит 180 дуговых градусов, значит, угол, опирающийся на диаметр, содержит 90 угловых градусов (черт. 334, б). 2. Угол, образованный касательной и хордой. Теорема. Угол, образованный касательной и хордой, измеряется половиной дуги, заключённой между его сторонами. Пусть / САВ составлен хордой СА и касательной АВ (черт. 335). Требуется доказать, что он измеряется половиной 1. На чертеже 336 найти касательные к окружности блоков. 2. По чертежу 337, а доказать, что угол АDС измеряется полусуммой дуг АС и ВК. 3. По чертежу 337, б доказать, что угол АМВ измеряется полуразностью дуг АВ и СЕ. 4. Через точку А, лежащую внутри круга, с помощью чертёжного треугольника провести хорду так, чтобы она в точке А разделилась пополам. 5. С помощью чертёжного треугольника разделить дугу на 2, 4, 8. равных частей. 6. Описать данным радиусом окружность, проходящую через две данные точки. Сколько решений имеет задача? 7. Сколько окружностей можно провести через данную точку? 💡 ВидеоМатематика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  №17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать  #207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать  Через любую точку, лежащую вне окружности ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать  Окружность. 7 класс.Скачать  Углы в окружности | ФормулыСкачать  2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать  Углы, связанные с окружностьюСкачать  Вписанные и центральные углыСкачать  ✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать  ЕГЭ-2020. №16. Вневписанная окружность🚀 Ортоцентр. Теорема Карно, Бланшета, Чевы, Менелая🔥Скачать  #26. EGMO-2022, Problem 6Скачать  |












































 АС содержит 60° 18′, то / В содержит 30°9′.
АС содержит 60° 18′, то / В содержит 30°9′.