Центр окружностей о1 и о2

Видео:Геометрия Две окружности радиуса R с центрами O1 и O2 касаются друг друга. Их пересекает прямаяСкачать

Ваш ответ

Видео:Геометрия Две окружности с центрами O1 и O3 и радиусами 4,5 и 2,5 касаются друг с другом внешнимСкачать

решение вопроса

Видео:Геометрия Окружности с центрами в точках O1 и O2 не имеют общих точек. Внутренняя общая касательнаяСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,845
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Г: Три равные окружности с центрами О1, О2, О3 и радиусом R попарно касаются друг друга в точках А ВСкачать

Две окружности с центрами О1 и О2, радиусы у которых равны пересекаются в точках M и N, через точку М проведена прямая параллельной О1О2 и пересекающая окружность с центром О2 в точке Д?

Геометрия | 5 — 9 классы

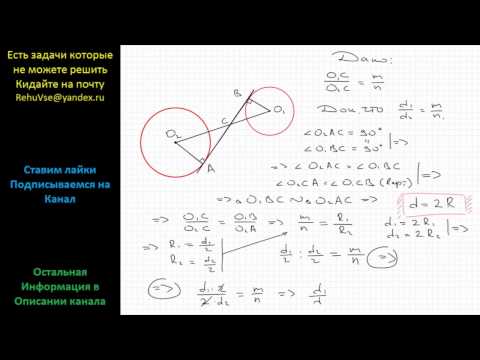
Две окружности с центрами О1 и О2, радиусы у которых равны пересекаются в точках M и N, через точку М проведена прямая параллельной О1О2 и пересекающая окружность с центром О2 в точке Д.

Используя переллельный перенос докажите , что четырехугольник О1МДО2 является параллелограммом.

О1М и О2Д — радиусы равных окружностей.

Следовательно, они равны.

Опустив перпендикуляры Ма из М и Дн из Д на прямую О1О2, получим равные между собой отрезки, ониравные также высоте четырехугольника О1О2ДМ.

Прямоугольные треугольники О1аМ и О2нД равны по гипотенузе и катету, и их основания лежат на одной прямой.

Сдвигая окружность О1 по прямой О1О2, получим совмещениеО1 и О2, т.

Совпадут и перпендикулярные отрезки между прямыми, опущенные из точек пересечения радиусов с окружностью.

Расстояние между их вершинами М и Д, О1 и О2 равны.

Следовательно, МД = О1О2.

Четырехугольник, в котором стороны попарно равны и параллельны, — параллелограмм

Четырехугольник О1МДО2 является параллелограммом, что и требовалось доказать.

Видео:Общая хорда двух окружностейСкачать

Докажите что если две окружности с центрами О и О1 пересекаются в точках А и В, то АВ _|_ ОО1?

Докажите что если две окружности с центрами О и О1 пересекаются в точках А и В, то АВ _|_ ОО1.

Видео:Уравнение окружности с центром на оси абсцисс, ординат или в начале координат. Урок 3. Геометрия 8.Скачать

Диагонали ромба «abcd» пересекаются в точке «о» ?

Диагонали ромба «abcd» пересекаются в точке «о» .

Докажите , что прямая «bd» касается окружности с центром «а» и радиусом , равным «ос».

Видео:Теорема о числе точек пересечения двух окружностейСкачать

Диагонали ромба АВСD пересекаются в точке О?

Диагонали ромба АВСD пересекаются в точке О.

Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС.

Видео:1 2 4 сопряжение окружностейСкачать

Две окружности с равными радиусами пересекаются в двух точках?

Две окружности с равными радиусами пересекаются в двух точках.

Докажите, что их общая хорда перпендикулярна к отрезку, соединяющему центры окружностей.

Видео:9.50.1. Планиметрия. Гордин Р.К.Скачать

Докажите, что прямая, проходящая через центр окружности, пересекает окружность в двух точках?

Докажите, что прямая, проходящая через центр окружности, пересекает окружность в двух точках.

Видео:Два кольца из разных проводников с центрами в точках O1 и O2 соединены, как показано на рисункеСкачать

Две окружности равных радиусов пересекаются в точках А и В?

Две окружности равных радиусов пересекаются в точках А и В.

Докажите, что отрезок, соединяющий центры окружностей, перпендикулярен АВ.

Видео:Геометрия. 8 класс. Урок 02 Касательные к окружностиСкачать

Через точку А к окружности проведены касательная АБ и секущая, которая пересекает окружность в точках E и F и проходит через центр окружности?

Через точку А к окружности проведены касательная АБ и секущая, которая пересекает окружность в точках E и F и проходит через центр окружности.

Найдите радиус окружности если AB = 12, а AF = 18.

Видео:ЕГЭ Задание 16 Комбинация трёх окружностейСкачать

Окружности радиусов 4 и 3, расстояние между центрами которых равно 5, пересекаются в точках А и В?

Окружности радиусов 4 и 3, расстояние между центрами которых равно 5, пересекаются в точках А и В.

Через точку В проведена прямая, пересекающая большую окружность в точке С, а меньшую в точке D ( точка В лежит между С и D).

Опредилите косинусы углов треугольника АСD.

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Через концы диаметра AB окружности с центром О, проведены параллельные прямые, пересекающие окружность в точках М и К?

Через концы диаметра AB окружности с центром О, проведены параллельные прямые, пересекающие окружность в точках М и К.

Докажите, что МК — диаметр окружности.

С рисунком, пожалуйста!

Видео:Геометрия 16-06. Взаимное расположение двух и более окружностей. Задача 6Скачать

Две окружности пересекаются в точках P и Q?

Две окружности пересекаются в точках P и Q.

Через точку A первой окружности проведены прямые AP и AQ, пересекающие вторую окружность в точках B и C.

Докажите, что касательная в точке A к первой окружности параллельна прямой BC.

На странице вопроса Две окружности с центрами О1 и О2, радиусы у которых равны пересекаются в точках M и N, через точку М проведена прямая параллельной О1О2 и пересекающая окружность с центром О2 в точке Д? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

У параллелограмма противоположные стороны равны и параллельны Если у четырехугольника противоположные стороны равны и параллельны то это параллелограмм если суммы противоположных сторон четырехугольника равны, то в такой четырехугольник можно вписать..

Например теорема Виета и теорема обратная теореме Виета.

Применены : свойства правильной четырёхугольной усеченной пирамиды, теорема Пифагора.

Нет, так как AC меньше BC.

У равнобедренного треугольника нет гипотенузы.

Треугольник FES = треугольникуSED по третьему признаку значит угол FES = углу SED и они равны по 45°. Угол FSE равен углу DSE и они равны по 90°. Угол SDE равен углу SFE и равны они по 45°.

А) ZAOB = 44° + 77° = 121°. Б) ZAOB = 12°37′ + 108 25 = 121°2′. Ответ, а) 121° ; б) 121°2′.

Видео:Геометрия В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимноСкачать

Сопряжение двух заданных окружностей

При решении задач на сопряжение двух окружностей следует учитывать, что множества точек плоскости, удаленных от этих окружностей на равные расстояния, представляют собой концентрические окружности, радиусы которых равны сумме или разно­сти радиуса заданной окружности и радиуса сопряжения. Точка пересечения этих окружностей есть центр сопряжения. Точки со­пряжения определяются как точки пересечения прямых, соеди­няющих центры заданных окружностей с центром сопряжения.

Пусть заданы окружности с центрами в точках О₁ и О₂ (рис. 1.26), имеющие радиусы R₁ и R₂ соответственно. Требуется выполнить внешнее сопряжение этих окружностей дугой окруж­ности радиусом R_с.

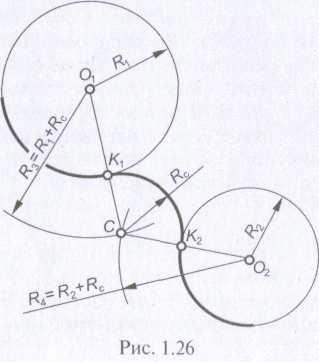
Из центра О₁ проводят дугу окружности радиусом R₃, рав­ным сумме радиусов R₁ и R₂, а из центра О₂ — дугу окружнос­ти радиусом R₄, равным сумме радиусов R₂ и R_с. Точка С пере­сечения этих дуг является цент­ром сопряжения, а точки К₁ и К₂ пересечения прямых О₁С и О₂С с соответствующими окружнос­тями — точками сопряжения. Оп­ределив основные параметры сопряжения, можно из центра С между точками К₁ и К₂ провести дугу окружности радиусом R_с.

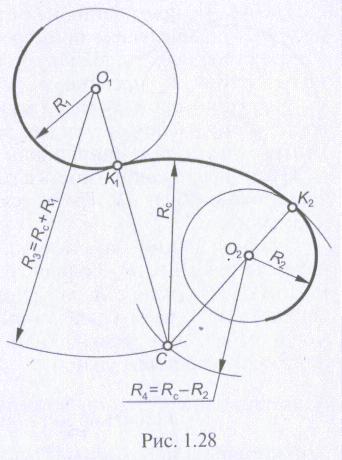
Если необходимо выполнить внутреннее сопряжение окруж­ностей с радиусами R₁ и R₂ и центрами в точках О₁ и О₂ (рис. 1.27), то для определения центра их сопряжения С надо про­вести дуги окружностей радиусами R₃ и R₄, равными разностям радиуса сопряжения R_с и соответственно радиусов R₁ и R₂ задан­ных окружностей. Точки К₁ и К₂ сопряжения находятся на продол­жении прямых, соединяющих центр сопряжений С с центрами окружностей О₁ и О₂.

Если же радиус сопряжения R_с задан (рис. 1.28) и для одной из окружностей (с центром О₁ и радиусом R₁) следует выполнить внутреннее сопряжение, а для другой (с центром О₂ и радиусом R₂) — внешнее, то для определения центра сопряжения С надо из точки О₁ провести дугу окружности радиусом R₃, равным сумме радиуса сопряжения R_с и радиуса окружности R₁ , а из точки О₂ -дугу окружности радиусом R₄, равным разности радиуса сопря­жения R_с и радиуса окружности R₂. При этом точка сопряжения К₁ будет находиться на пересечении прямой О₁С с окружностью, имеющей радиус R₁ , а точка сопряжения К₂— на пресечении ок­ружности, имеющей радиус R₂, с продолжением прямой О₂С.

🎦 Видео

Урок 47. Взаимное расположение окружностей (8 класс)Скачать

[7] Окружности с нуля для ЕГЭ по математике. Внешнее касание окружностей. Конструкция из демоверсии.Скачать

9.52.1. Планиметрия. Гордин Р.К.Скачать

КАСАЮЩИЕСЯ ОКРУЖНОСТИСкачать

Геометрия 16-02. Взаимное расположение двух и более окружностей. Задача 2Скачать