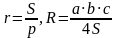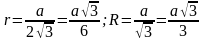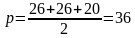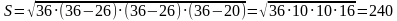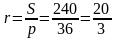Вписанная окружность решение задач по готовым чертежами

Задачи на вписанные и центральный углы, на касательную, на вписанные и описанные четырехугольники.

Видео:Геометрия 8 класс : Решение задач. Вписанная окружностьСкачать

Скачать:

Видео:Вписанная и описанная окружности. ЗадачиСкачать

Предварительный просмотр:

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее (на рисунке это угол ВАС ).

Центральный угол – это угол, вершина которого находится в центре окружности, а стороны пересекают ее (на рисунке это угол ВОС )

1. Вписанный угол равен половине градусной меры дуги, на которую он опирается.
2. Центральный угол равен градусной мере дуги, на которую он опирается.
3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
4. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
5. Вписанный угол, опирающийся на диаметр равен 90°.

Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 8.

В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 130∘. Найдите вписанный угол ACB. Ответ дайте в градусах.

Точка О — центр окружности, ∠ BOC=160° (см. рисунок). Найдите величину угла BAC (в градусах).

На окружности с центром O отмечены точки A и B так, что ∠AOB=140∘. Длина меньшей дуги AB равна 98. Найдите длину большей дуги.

Точка О — центр окружности, ∠BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).

Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25∘. Найдите величину угла BOC. Ответ дайте в градусах.

На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠ NBA=38∘. Найдите угол NMB. Ответ дайте в градусах.

В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.

Касательная окружности — прямая, имеющая с окружностью единственную общую точку

1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания
2. Отрезки касательных проведенных из одной точки, равны

Вписанные и описанные четырехугольники

Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна 180 0

Четырехугольник можно описать около окружности тогда и только тогда, когда суммы длин его противоположных сторон раны

Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 84∘. Найдите величину угла OMK. Ответ дайте в градусах.

Два угла вписанного в окружность четырехугольника равны 82 0 и 58 0 . Найдите больший из оставшихся углов. Ответ дайте в градусах.

В угол C величиной 40∘ вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.

В трапецию, сумма длин боковых сторон которой равна 22, вписана окружность. Найдите длину средней линии трапеции.

К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон

Отрезок AB=48 касается окружности радиуса 14 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 130°.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

По теме: методические разработки, презентации и конспекты

Сборник УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ Параллельные прямые.

Сборника УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ «Параллельные прямые» содержит 58 задач по теме. Задания пособия предназначены, прежде всего, для обучения школьников решению задач по только что изученному.

Задачи и упражнения на готовых чертежах 7 класс — Геометрия 7-9 класс Е.М. Рабинович, 2007 г.

Задачи и упражнения на готовых чертежах 7 класс — Геометрия 7-9 класс Е.М. Рабинович, 2007 г.

Задачи для решения по готовым чертежам в 9 классе по теме «Длина окружности»

Задания для повторения и закрепления формул длины окружности, длины дуги окружности, для применения формул вычисления радиуса окружности через стороны правильного многоугольника, задания для самостоят.

Презентация по теме «Касательная к окружности — задачи на готовых чертежах»

Данная презентация содержит 9 задач на готовых чертежах по теме «Касательная к окружности». Решение каждой задачи появляется на чертеже по щелчку (анимация) постепенно. Это дает возможность проработат.

Самостоятельная работа на готовых чертежах по теме «Касательная к окружности.»

Самостоятельная работа на 10 минут, может использоваться после изучения темы в 8 классе или для повторения при подготовке к ОГЭ.

Задачи по теме «Окружность» на готовых чертежах для 8-9 классов.

Карточки по геометрии для устной, самостоятельной или проверочной работ.

Задачи по геометрии на готовых чертежах для 8-9 классов.

Задачи по геометрии на готовых чертежах позволяют не тратить время на построение, чтение условия задачи. Их можно использовать для повторения материала, устного опроса, самостоятельной работы.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Решение задач по теме «Вписанная и описанная окружности»

Урок №7. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.

Просмотр содержимого документа
«Решение задач по теме «Вписанная и описанная окружности»»

Тема: Решение задач по теме «Вписанная и описанная окружности»

Задачи: продолжить формирование навыков решения задач по теме.

Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.

Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.

Формулы нахождения радиуса вписанной r и описанной R около треугольника окружностей.

Для любого треугольника:

Для равностороннего треугольника.

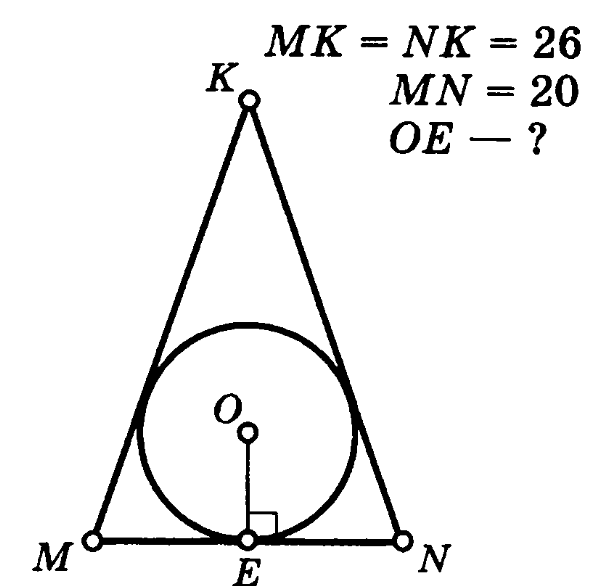
Задача 1. В равнобедренном треугольнике MKN боковые стороны равны 26, а основание – 20. В треугольник вписана окружность с радиусом ОЕ. Найти длину ОЕ.

Решение (краткое). Радиус окружности, вписанной в равнобедренный треугольник можно вычислить по стандартной формуле 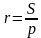, где р – полупериметр.

Ответ: .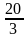

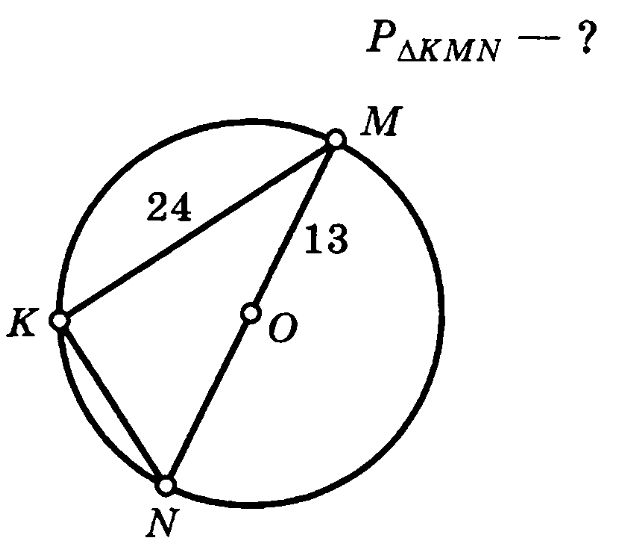
Задача 2. Прямоугольный треугольник KMN описан около окружности радиуса 13. Один из катетов треугольника равен 24. Найти периметр треугольника.

Решение (краткое). MN=d=2r=26, по теореме Пифагора KN=10, Р=60.

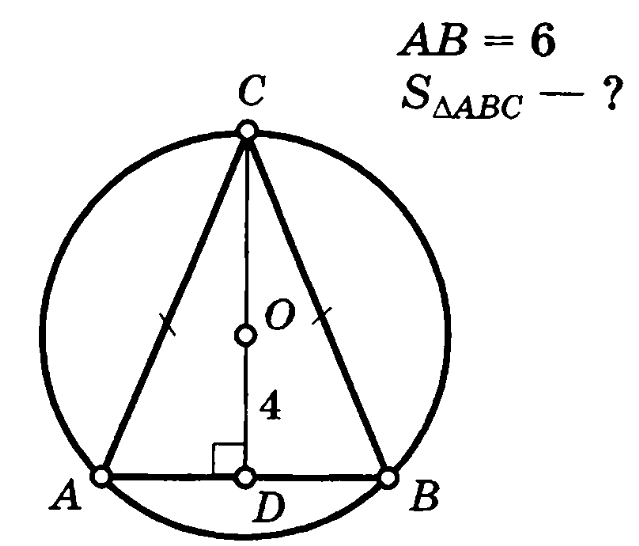
Задача 3. Равнобедренный треугольник АВС вписан в окружность, отрезок ОD=4. Найти площадь треугольника.

Решение (краткое). ОВ=5, ОС=ОВ=5, СD=9, S=0.5*9*6=27.

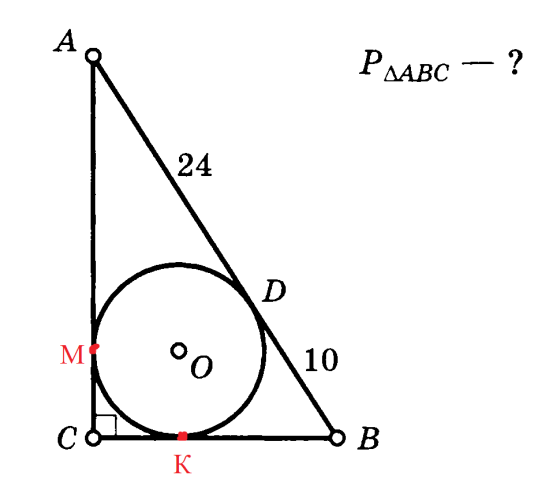
Задача 4. Прямоугольный треугольник описан около окружности. Точка D делит гипотенузу на две части, длинами по 10 и 24. Найти периметр треугольника.

Решение (краткое). DB=DK=10, AD=AM=24.

KOMC – квадрат, т.к. ОК перпендикулярен СВ, ОМ перпендикулярен АС и KC=CM, OK=OM=r.

Пусть KC=CM=х, тогда ВС=10+х, АС=24+х, АВ=24+10=34.

Видео:Решение задач по теме "Вписанная и вневписанная окружность"Скачать

Презентации по геометрии на тему: «Задачи по готовым чертежам(окружность). Готовимся к ЕГЭ и ГИА»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Вписанная окружность.ppt

Описание презентации по отдельным слайдам:

Найдите радиус окружности, вписанной в квадрат со стороной 4. ОТВЕТ: 2 Найдите сторону квадрата, описанного около окружности радиуса 4. ОТВЕТ: 8

Найдите радиус r окружности, вписанной в четырехугольник АВСД. Считайте, что стороны квадратных клеток равны 1. В ответе укажите r√10 . ОТВЕТ: 5

Сторона ромба равна 1, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба. ОТВЕТ: 0,25 Острый угол ромба равен 30°. Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба. ОТВЕТ: 8

Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника. ОТВЕТ: 6 Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника. ОТВЕТ: 24

Сторона правильного треугольника равна √3. Найдите радиус окружности, вписанной в этот треугольник. Радиус окружности, вписанной в правильный треугольник, равен √3/6. Найдите сторону этого треугольника. ОТВЕТ: 0.5 ОТВЕТ: 1

Катеты равнобедренного прямоугольного треугольника равны 2 + √2. Найдите радиус окружности, вписанной в этот треугольник. В треугольнике АВС АС = 4, ВС = 3, угол С равен 90°. Найдите радиус вписанной окружности. ОТВЕТ: 1 ОТВЕТ: 1

Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь. ОТВЕТ: 30

Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен √3. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной √3. ОТВЕТ: 2 ОТВЕТ: 1,5

Периметр четырехугольника, описанного около окружности, равен 24, две его стороны равны 5 и 6. Найдите большую из оставшихся сторон. 5 6 х 13 – х ОТВЕТ: 7 АВ + СД = АД + ВС

Выбранный для просмотра документ Касательная, хорда, секущая.ppt

Описание презентации по отдельным слайдам:

Касательная, хорда, секущая (задачи В8)

1. Найдите хорду, на которую опирается угол 90°, вписанный в окружность радиуса 1. ОТВЕТ: 2

2. Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса √3. ОТВЕТ: 3

3. Хорда АВ делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки С, принадлежащей меньшей дуге окружности? Ответ дайте в градусах. ОТВЕТ: 105

ОТВЕТ: 46 4. Хорда АВ стягивает дугу окружности в 92°. Найдите угол АВС между этой хордой и касательной к окружности, проведенной через точку В. Ответ дайте в градусах. 92° 88° 44° Или свойство: Угол между касательной и хордой равен половине дуги, стягиваемой хордой.

5. Угол между хордой АВ и касательной ВС к окружности равен 32°. Найдите величину меньшей дуги, стягиваемой хордой АВ . Ответ дайте в градусах. ОТВЕТ: 64

ОТВЕТ: 118 6. Через концы А, В дуги окружности в 62° проведены касательные ВС и АС. Найдите угол ВСА. Ответ дайте в градусах.

ОТВЕТ: 26 7. Найдите угол АСО, если его сторона АС касается окружности, О – центр окружности, а меньшая дуга окружности АВ, заключенная внутри этого угла, равна 64°. Ответ дайте в градусах.

ОТВЕТ: 62 8. Угол АСО равен 28°, где О – центр окружности. Его сторона АС касается окружности. Найдите величину меньшей дуги АВ окружности, заключенной внутри этого угла. Ответ дайте в градусах. 28°

9. Найдите угол АСО, если его сторона АС касается окружности, О – центр окружности, а большая дуга АД окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах. 116° ? ОТВЕТ: 26

10. Угол АСО равен 24°. Его сторона АС касается окружности. Найдите градусную величину большей дуги АД окружности, заключенной внутри этого угла. Ответ дайте в градусах. 24° ? ОТВЕТ: 114

Выбранный для просмотра документ Описанная окружность.ppt

Описание презентации по отдельным слайдам:

1. Сторона правильного треугольника равна √3. Найдите радиус окружности, описанной около этого треугольника. ОТВЕТ: 1 2. Радиус окружности, описанной около правильного треугольника, равен √3. Найдите сторону этого треугольника. ОТВЕТ: 3

ОТВЕТ: 1 4. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника. 3. Сторона АВ треугольника АВС равна 1. Противолежащий ей угол С равен 150°. Найдите радиус окружности, описанной около этого треугольника. ОТВЕТ: 2

ОТВЕТ: 25 5. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника. 6. В треугольнике АВС ВС = 6, угол С равен 90°. Радиус описанной окружности этого треугольника равен 5. Найдите АС. ОТВЕТ: 8

ОТВЕТ: 60 7. Точки А, В, С, Д, расположенные на окружности, делят эту окружность на четыре дуги АВ, ВС, СД и ДА, градусные величины которых относятся соответственно как 4 : 2 : 3 : 6. Найдите угол А четырехугольника АВСД. Ответ дайте в градусах.

ОТВЕТ: 2,5 8. Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 3 и 4. 9. Меньшая сторона прямоугольника равна 6. Угол между диагоналями равен . Найдите радиус описанной окружности этого прямоугольника. ОТВЕТ: 6

10. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах. ОТВЕТ: 122

11. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции. ОТВЕТ: 7

12. Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности. 13. Около окружности, радиус которой равен √3/2, описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника. ОТВЕТ: 24 ОТВЕТ: 1

14. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 54°. Найдите n. ОТВЕТ: 5

Краткое описание документа:

Очень полезно использовать различные иллюстрации, демонстрировать их во время урока. Это упрощает работу учителя, ведь он не тратит лишнее время на записи на доске. Тем самым появляется дополнительное время для лучшего закрепления урока, для дополнительных практических заданий.

Данные презентации предназначены для отработки и закрепления знаний по темам «Касательная к окружности», «Описанная и вписанная окружности». Эти презентации можно использовать не только при подготовки к экзаменам в 9 и 11 классах, но и на уроках при закреплении материала в 8 и 9 классах.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 954 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 684 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 507 068 материалов в базе

Другие материалы

• 14.05.2015
• 982
• 0

• 14.05.2015
• 3004
• 25

• 14.05.2015
• 1648
• 0

• 14.05.2015
• 900
• 0

• 14.05.2015
• 6500
• 6

• 14.05.2015
• 1640
• 0

• 14.05.2015
• 8641
• 38

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 14.05.2015 9081
• RAR 678.9 кбайт
• 18 скачиваний
• Рейтинг: 1 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Сальникова Татьяна Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 6 месяцев
• Подписчики: 0
• Всего просмотров: 13805
• Всего материалов: 5

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Опубликованы проекты ФГОС по специальностям СПО

Время чтения: 2 минуты

Минпросвещения намерено решить вопрос с третьей сменой в школах в 2023 году

Время чтения: 1 минута

В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу

Время чтения: 1 минута

Проверки показали невыполнение в ряде регионов санитарных правил в школах

Время чтения: 1 минута

Новые курсы: педагогический дизайн, ФГОС 2021, управление школой и другие

Время чтения: 14 минут

Школы Пскова перевели на дистанционное обучение

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💥 Видео

8 класс, 38 урок, Вписанная окружностьСкачать

Вписанная окружностьСкачать

Геометрия 8 класс. Тема: "Вписанная и описанная окружности. Решение задач"Скачать

ВПИСАННАЯ ОКРУЖНОСТЬ радиус 8 класс АтанасянСкачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Геометрия 9 класс. Вписанные и описанные окружности. Ключевая задача № 4.Скачать

ГЕОМЕТРИЯ 8 класс: Решение задач. Описанная окружностьСкачать

Вписанная и описанная окружностиСкачать

ВПИСАННАЯ окружность ОПИСАННАЯ окружность радиус 8 классСкачать

Вписанная окружность. ЗАДАЧА ИЗ ГОНКОНГА!Скачать

Вписанная окружностьСкачать

Урок по теме ВПИСАННАЯ ОКРУЖНОСТЬСкачать