Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть
- Почему так важно определять какой четверти принадлежит угол?
- Про непостоянство четвертей:
- Как посчитать длину окружности
- Онлайн калькулятор
- Как посчитать длину окружности зная диаметр
- Формула
- Пример
- Как посчитать длину окружности зная радиус
- Формула
- Пример
- Как посчитать длину окружности зная её площадь
- Формула
- Пример
- Деление круга на равные части
- Деление круга на равные по площади части радиусами
- Деление круга на равные по площади части параллельными хордами
- Деление круга на равные части радиусами
- Деление круга на равные части параллельными хордами
- 📽️ Видео
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Почему так важно определять какой четверти принадлежит угол?
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
 ((0;-) (frac) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:Радиус и диаметрСкачать  Как посчитать длину окружностиВидео:Как искать точки на тригонометрической окружности.Скачать  Онлайн калькуляторКак посчитать длину окружности зная диаметрКакая длина у окружности если Какова длина окружности (С) если её диаметр d? ФормулаС = π⋅d , где π ≈ 3.14 ПримерЕсли диаметр круга равен 1 см, то его длина примерно равна 3.14 см. Как посчитать длину окружности зная радиусКакая длина у окружности если Какова длина окружности (С) если её радиус r? ФормулаС = 2⋅π⋅r , где π ≈ 3.14 ПримерЕсли радиус круга равен 0.5 см, то его длина примерно равна 3.14 см. Как посчитать длину окружности зная её площадьКакая длина у окружности если Какова длина окружности (С) если её площадь S? ФормулаС = 2π⋅ √ S /π , где π ≈ 3.14 ПримерЕсли площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см. Видео:Длина окружности. Площадь круга. 6 класс.Скачать  Деление круга на равные частиСтатья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами. Деление круга на равные по площади части радиусамиДеление круга на равные по площади части параллельными хордамиДеление круга на равные части радиусамиТрадиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:
Собственно и всё — мы получили все характеристики для N равных секторов Деление круга на равные части параллельными хордамиЭтот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично. Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева. Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности. По теореме Пифагора получаем следующую функцию Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна: Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем Итак, полное выражение Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности) Таким образом мы можем приравнять Что дает нам такое финальное уравнение Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона. Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее. Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды. 📽️ ВидеоМатематика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать  Длина окружности. Математика 6 класс.Скачать  Деление окружности на 3; 6; 12 равных частейСкачать  5 класс, 22 урок, Окружность и кругСкачать  Окружность. Круг. 5 класс.Скачать  Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать  Тригонометрическая окружность. Как выучить?Скачать  Длина окружности. Площадь круга - математика 6 классСкачать  3 четверть. 9 класс. Алгебра. Углы на единичной окружностиСкачать 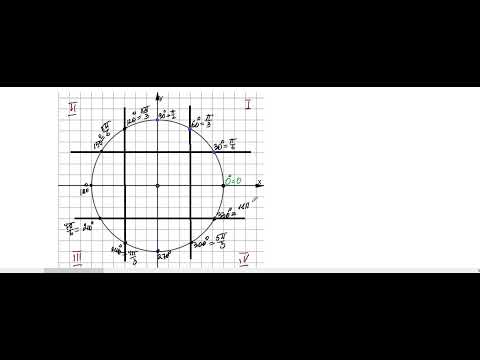 Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  Окружность. Как найти Радиус и ДиаметрСкачать  В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать  Площадь круга. Математика 6 класс.Скачать  Репетитор по математике. Доли. Нахождение доли от числаСкачать  +Как найти длину окружностиСкачать  |


