Треугольники конгруэнтны что значит

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Содержание:

В соответствиев геометрии означает, что если две плоские фигуры имеют одинаковую форму и размеры, они конгруэнтны. Например, два сегмента совпадают, если их длины равны. Точно так же конгруэнтные углы имеют одинаковую меру, даже если они не ориентированы одинаково на плоскости.

Термин «конгруэнтность» происходит от латинского конгруэнтный, значение которого — соответствие. Таким образом, две совпадающие фигуры точно соответствуют друг другу.

Например, если мы наложим на изображение два четырехугольника, мы обнаружим, что они совпадают, поскольку расположение их сторон одинаково и их размеры совпадают.

Поместив четырехугольники ABCD и A’B’C’D один поверх другого, фигуры будут точно совпадать. Соответствующие стороны называются гомологические стороны или соответствующий и для выражения соответствия используется символ. Тогда мы можем подтвердить, что ABCD ≡ A’B’C’D ’.

Видео:Конгруэнтность (равенство) треугольниковСкачать

Критерии конгруэнтности

Следующие характеристики являются общими для конгруэнтных многоугольников:

-Той же формы и размера.

-Идентичные измерения их углов.

— Одинаковая мера с каждой стороны.

В случае, если два рассматриваемых многоугольника являются правильными, то есть все стороны и внутренние углы имеют одинаковые размеры, совпадение обеспечивается, когда любой из следующих условий:

-The апофемы у них такая же мера

-The радио меры каждого многоугольника равны

Апофема правильного многоугольника — это расстояние между центром и одной из сторон, а радиус соответствует расстоянию между центром и вершиной или углом фигуры.

Критерии согласованности часто используются, потому что многие детали и детали всех видов производятся серийно и должны иметь одинаковую форму и размеры. Таким образом, их можно легко заменить при необходимости, например, гайки, болты, листы или брусчатку на земле на улице.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Соответствие, идентичность и сходство

Есть геометрические понятия, связанные с конгруэнтностью, например идентичные цифры и похожие цифры, что не обязательно означает, что цифры совпадают.

Обратите внимание, что конгруэнтные фигуры идентичны, однако четырехугольники на рисунке 1 могут быть по-разному ориентированы на плоскости и при этом оставаться конгруэнтными, поскольку различная ориентация не меняет размер их сторон или их углы. В этом случае они больше не будут идентичными.

Другая концепция заключается в сходстве фигур: две плоские фигуры подобны, если они имеют одинаковую форму и их внутренние углы равны, хотя размеры фигур могут быть разными. В этом случае цифры не совпадают.

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Примеры сравнения

Видео:Треугольники. 7 класс.Скачать

— Соответствие углов

Как мы указали в начале, конгруэнтные углы имеют одинаковую меру. Есть несколько способов получить конгруэнтные углы:

Видео:Признаки равенства треугольников. 7 класс.Скачать

Пример 1

Две линии с общей точкой определяют два угла, называемые Противоположные углы при вершине. Эти углы имеют одинаковую меру, поэтому они совпадают.

Видео:КОНГРУЭНТНОСТЬ простыми словамиСкачать

Пример 2

Две параллельные линии плюс одна линия т что пересекает их обоих. Как и в предыдущем примере, когда эта линия пересекает параллели, она образует совпадающие углы, по одному на каждой линии с правой стороны и еще по два с левой стороны. На рисунке показаны α и α₁, справа от линии т, которые конгруэнтны.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Пример 3

В параллелограмме четыре внутренних угла, которые равны двум и двум. Они находятся между противоположными вершинами, как показано на следующем рисунке, на котором два угла, отмеченные зеленым цветом, совпадают, а также два угла, отмеченные красным.

Видео:Конгруэнтность что это такое простыми словами || Как стать конгруэнтнымСкачать

— Конгруэнтность треугольников

Два треугольника одинаковой формы и размера конгруэнтны. Чтобы проверить это, есть три критерия, которые можно исследовать в поисках совпадения:

–Критерий LLL: три стороны треугольников имеют одинаковые размеры, поэтому L₁ = L ’₁; L₂ = L ’₂ и я₃ = L ’_3.

–Критерии ALA и AAL: Треугольники имеют два равных внутренних угла, и сторона между этими углами имеет одинаковую величину.

–Критерий LAL: две стороны идентичны (совпадают) и между ними одинаковый угол.

Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Решенные упражнения

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

— Упражнение 1

На следующем рисунке показаны два треугольника: ΔABC и ΔECF. Известно, что AC = EF, AB = 6 и CF = 10. Кроме того, углы ∡BAC и ∡FEC совпадают, а углы ∡ACB и ∡FCB также совпадают.

Тогда длина отрезка BE равна:

Видео:41 Признаки конгруэнтности треугольниковСкачать

Решение

Поскольку два треугольника имеют сторону равной длины AC = EF, заключенную между равными углами ∡BAC = ∡CEF и ∡BCA = ∡CFE, можно сказать, что два треугольника совпадают по критерию ALA.

То есть ΔBAC ≡ ΔCEF, поэтому мы должны:

Но рассчитываемый отрезок: BE = BC — EC = 10-6 = 4.

Итак, правильный ответ (iii).

Видео:Свойства равнобедренного треугольника. Признаки конгруэнтности (равенства) треугольниковСкачать

— Упражнение 2.

На рисунке ниже показаны три треугольника. Также известно, что два указанных угла составляют 80º каждый и что отрезки AB = PD и AP = CD. Найдите значение угла X, указанного на рисунке.

Видео:Математика, 10-й класс, Треугольники. Классификация треугольников. Конгруэнтные треугольникиСкачать

Решение

Вы должны применить свойства треугольников, которые подробно описываются шаг за шагом.

Видео:Определение преобразований | Геометрические преобразования и Конгруэнтность | ГеометрияСкачать

Шаг 1

Начиная с критерия конгруэнтности треугольника LAL, можно сказать, что треугольники BAP и PDC конгруэнтны:

Видео:Конгруэнтность (равенство) треугольниковСкачать

Шаг 2

Сказанное выше приводит к утверждению, что BP = PC, поэтому треугольник ΔBPC равнобедренный и ∡PCB = ∡PBC = X.

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Шаг 3

Если называть угол BPC γ, то получаем:

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Шаг 4

И если мы назовем углы APB и DCP β и α углами ABP и DPC, то получим:

α + β + γ = 180º (поскольку APB — плоский угол).

Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Шаг 5

Кроме того, α + β + 80º = 180º на сумму внутренних углов треугольника APB.

Видео:Конгруэнтные треугольникиСкачать

Шаг 6

Объединяя все эти выражения, мы получаем:

Шаг 7

Шаг 8

Наконец, следует, что:

Ссылки

1. Балдор А. 1973. Плоская и космическая геометрия. Центральноамериканская культура.
2. Фундамент СК-12. Конгруэнтные многоугольники. Получено с: ck 12.org.
3. Наслаждайтесь математикой. Определения: Радиус (многоугольник). Получено с: Enjoyylasmatematicas.com.
4. Открытый справочник по математике. Тестирование полигонов на соответствие. Получено с: mathopenref.com.
5. Википедия. Конгруэнтность (геометрия). Получено с: es.wikipedia.org.
6. Сапата, Ф. Треугольники, история, элементы, классификация, свойства.Получено с: lifeder.com.

Сумма многочленов, как это сделать, примеры, упражнения

Гиперлексия: симптомы, причины и лечение этого синдрома

Разница между конгруэнтным и равным

Конгруэнтный против равного Конгруэнтность и равенство — схожие понятия в геометрии, но их часто неправильно понимают и путают.РавноРавный означает, что величины или размеры любых двух сравниваемых о

Содержание:

Конгруэнтный против равного

Конгруэнтность и равенство — схожие понятия в геометрии, но их часто неправильно понимают и путают.

Равно

Равный означает, что величины или размеры любых двух сравниваемых одинаковы. Концепция равенства знакома в нашей повседневной жизни; однако как математическое понятие его следует определять с помощью более строгих мер. В разных полях используется другое определение равенства. В математической логике это определяется с помощью аксиом Паэно. Равенство относится к числам; часто числа, представляющие свойства.

В контексте геометрии равенство имеет те же значения, что и в обычном использовании термина «равно». В нем говорится, что если атрибуты двух геометрических фигур одинаковы, то эти две фигуры равны. Например, площадь треугольника может быть равна площади квадрата. Здесь речь идет только о размере «площади» собственности, и они совпадают. Но сами цифры нельзя считать одинаковыми.

Конгруэнтный

В контексте геометрии конгруэнтность означает равенство как фигур (формы), так и размеров. Или, проще говоря, если одно можно рассматривать как точную копию другого, тогда объекты конгруэнтны, независимо от их расположения. Это эквивалентное понятие равенства, используемое в геометрии. В случае сравнения в аналитической геометрии также даются гораздо более строгие определения.

Независимо от ориентации показанных выше треугольников, их можно расположить так, чтобы они полностью перекрывали друг друга. Следовательно, они одинаковы по размеру и форме. Следовательно, они являются конгруэнтными треугольниками. Фигура и ее зеркальное отображение также совпадают. (Их можно перекрывать после поворота вокруг оси, лежащей в плоскости формы).

В приведенном выше примере, хотя фигуры являются зеркальными отражениями, они совпадают.

Конгруэнтность в треугольниках важна при изучении геометрии плоскости. Чтобы два треугольника были равны, соответствующие углы и стороны должны быть равны. Треугольники можно считать конгруэнтными, если выполняются следующие условия.

• SSS (сторона сторона сторона)  если все три соответствующие стороны равны по длине.

• SAS (сторона бокового угла)  Пара соответствующих сторон и включенный угол равны.

• ASA (Угол стороны угла)  Пара соответствующих углов и включенная сторона равны.

• AAS (Angle Angle Side)  Пара соответствующих углов и не включенная сторона равны.

• HS (катет гипотенузы прямоугольного треугольника)  Два прямоугольных треугольника конгруэнтны, если гипотенуза и одна сторона равны.

Случай AAA (Angle Angle Angle) НЕ является случаем, когда соответствие всегда действительно. Например, следующие два треугольника имеют равные углы, но не совпадают, потому что размеры сторон разные.

В чем разница между конгруэнтным и равным?

• Если некоторые атрибуты геометрических фигур одинаковы по величине, то они считаются равными.

• Если и размеры, и фигуры равны, то цифры считаются совпадающими.

• Равенство касается величины (чисел), в то время как конгруэнтность касается как формы, так и размера фигуры.

Конгруэнтные фигуры

Конгруэнтные фигуры.

Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

§ 4. Конгруэнтные фигуры. А. М. Абрамов НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ.

П е р в о е о п р е д е л е н и е . Фигура Фх конгруэнтна фигуре
Ф, если существует сохраняющее расстояния отображение
фигуры Ф на Фх.
Так как перемещения сохраняют расстояния, часто употребляется
такой метод доказательства конгруэнтности фигур Ф и Фх:
находится перемещение, при котором образом фигуры Ф является
Фх.
В т о р о е о п р е д е л е н и е . Если существует перемещение,
отображающее фигуру Ф на Фх, то говорят, что фигура Фх конгруэнтна
Ф.
Замечание, сделанное перед этим определением, показывает,
что если фигура Фх конгруэнтна фигуре Ф в смысле второго определения,
то Фх конгруэнтна Фив смысле первого определения.

257 Конгруэнтные фигуры.

Для доказательства эквивалентности этих двух определений
остается показать, что если существует сохраняющее расстояния
отображение G, область определения которого — фигура Ф, а
множество значений — Фх, то существует и перемещение F (изометрическое
отображение всей плоскости, а не ее подмножества Ф),
при котором образ фигуры Ф — фигура Фх.
Т е о р е м а 4.1. Для любого сохраняющего расстояния отображения
G произвольной фигуры Ф в плоскость существует перемещение
F, являющееся продолжением G на всю плоскость (для любой
точки X фигуры Ф имеем: F (X) — G (X)).
Д о к а з а т е л ь с т в о . Если Ф состоит из одной или двух
точек, то утверждение теоремы — очевидное следствие A.IV.1.
Рассмотрим другие возможности.
Первый случай: Ф — подмножество прямой.
Пусть А и В — различные точки Ф. Обозначим через Лх и Вг
образы точек А а В при отображении G. Так как G сохраняет расстояния,
|Лх5х1 = |Л5|. Вследствие А.IV.1. существует перемещение
F, переводящее А в Аъ В в Вх.
Отображения G и F сохраняют расстояния. Значит, G (Ф),
F (Ф) — подмножества прямой Л^. Возьмем отличную от Л и Б
точку Xфигуры Ф. НапрямойЛхбх имеется ровно одна точка Х1г
для которой |ЛХ| = |ЛхХх|, |fiX| =|SxXx|. Поэтому и F, и G
переводят X в X’, т. е. F — продолжение G на всю плоскость.
Второй случай: Ф содержит точки А, В, С, не принадлежащие
одной прямой.
Так как G сохраняет расстояния, точки Ах — G (Л), Вх — G (В),
Сх = G (С) также не принадлежат одной прямой, причем | Лх-SxN
= | АВ, |ВхСх1 = |ВС|, |ЛхСх1 =|ЛС|. Как показано при доказательстве
теоремы 2.1 существует перемещение F, которое, как и
С, переводит Л в Аг, В в Въ С в Сх. Если Ф не содержит других
точек, кроме Л, б и С, теорема доказана. Пусть X — произвольная
точка Ф, отличная от Л, Б, С.
В этом случае мы докажем, что F (X) = G (X), показав, что существует
не более одной точки плоскости, удаленной от Л’ на расстояние
| ЛХ|, от В’ — на |fiX| и от С’— на |СХ|.
В самом деле, имеется не более двух точек Y1 и Y» плоскости,
для каждой из которых расстояние от Ах равно |ЛХ|, а от Вх —
|£Х| (теорема 1.З.), причем эти точки симметричны относительно
прямой АВ. Но C’Y’^ | C’Y»: если эти расстояния равны, а
Y* ф Y», то С’ — точка меди-
атрисы к отрезку Y’Y», т. е.
С’ € (ЛхВх). Это противоречит
предположению С £ (АВ).
Надо добавить, что хотя приведенные
определения и эквивалентны,
числа, показывающие,
сколько имеется отображений,
устанавливающих конгруэнт

258 Конгруэнтные фигуры.

ность фигуры Ф фигуре Фх в смысле первого и второго определений,
могут оказаться различными. Так, с сохранением расстояний
отрезок на отрезок равной длины отображается двумя способами,
а перемещений, переводящих первый отрезок во второй, существует
четыре.
Так как перемещения плоскости образуют группу, сразу получаем:
У.4.1. Отношение конгруэнтности на множестве фигур является
отношением эквивалентности.
Отношение конгруэнтности фигур обозначается знаком е^.
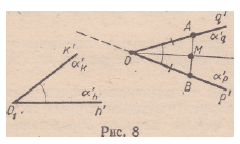
Т е о р е м а 4.2. Для любого луча р’ в заданной полуплоскости
а’ с границей р существует единственный луч q’, имеющий общее
начало с р’, такой, что угол p’q’ конгруэнтен данному углу h’k’.
Д о к а з а т е л ь с т в о . Если в полуплоскости а’ существует
такой луч q’, что Z. p’q’ ^ A.h’k’, то перемещение, отображающее
угол h’k’ на угол p’q’, переводит Ох в О (рис. 8), а луч h’ ,(или k’)
отображается на луч р’ при этом полуплоскость ah, содержащая k’
(соответственно полуплоскость а*, содержащая Н’), отображается
на а’р. как уже говорилось выше, при перемещениях крайние (граничные)
точки множества отображаются на крайние (граничные)
точки его образа. Таких перемещений в силу A.IV.2 имеется два.
Обозначим их через Ft и F%. Тогда
FAh’)=p’ f!«)=«;,
F2 (kr) = p’, F2 (a’) = a’.
Fi (k1) и F
g (p’) — искомые лучи. Теорема существования доказана.
Для доказательства единственности остается показать, что
Fy (k’) = F2 (h’). Обозначим через q’ луч Ft (k’). Возьмем на лучах
р’ и q’ точки А и В: ОА = В.
Симметрия относительно медиатрисы ОМ отрезка АВ переводит
р’ в q’, q’ в р’у а полуплоскость а’р, содержащую^ q — в полуплоскость
a’q, содержащую р’.
Рассмотрим перемещение Som ° Ft. Имеем:
Som о Fi (&’) = S0M (qr) = p’.
s om o F ,K) = sM(«;) = a;.
Итак, образы флага 0$a’k при перемещениях F2 и Som ° FL
совпадают. В силу единственности перемещения, отображающего
один из данных флагов на другой, Som ° Fx = F2. Так как F2 (h’) =
= (So.m 0 Fj) (h’) = Som (p ) = q’, теорема доказана.
Т е о р е м а 4.3. Если треугольники АуВ^Су и А2В.,С2 таковы,
что BiAjCi ^ Z. В2А2С2, AiBi = А2В2, AiCi== 1Л2С2!, то
АА2В2С2 ^ ААхВхСх.
Д о к а з а т е л ь с т в о . Так как Z-B^Cx ^ Z.B.2A2C2, существует
перемещение F, отображающее Ах на А2, луч АгВх на луч

259 Конгруэнтные фигуры.

А2Въ а луч Afix на луч Л2С2. Воспользовавшись условиями
AxBx| = | Л2В2|, AxCx| = 1Л2С21 и единственностью точки луча,
удаленной от его начала на данное расстояние, получаем, что
Аналогично доказываются другие признаки конгруэнтности
треугольников: по трем сторонам, по стороне и двум прилежащим
к ней углам.
О п р е д е л е н и е . Угол, конгруэнтный своему смежному, называется
прямым углом.
Для выпуклого угла имеются два угла, смежные с ним (рис. 9).
Поэтому вначале необходимо доказать корректность этого определения:
если Z.lg^Z.2, то Z . l ^ Z . 3 (рис. 9).
Угол 2 при симметрии Sa отображается на конгруэнтный ему
угол. Но луч ОА при симметрии Sa отображается на себя и по условию
Z. 1 Z. 2. Так как по теореме 4.2 от луча О А можно отложить
в данной полуплоскости лишь один угол, конгруэнтный данному,
$а _____
то [ОБ) ==> [ОС). Следовательно, и прямая р при симметрии Sa
отображается на’себя.
Из теоремы 3.4 вытекает, что Sp (а) — а. Поэтому угол 1 при
симметрии Sp отображается на угол 3, т. е. Z. 1 Ш АЗ.
Если две прямые пересекаются, то, как известно, они задают
четыре выпуклых угла. Из доказанной корректности определения
прямого угла следует, что если один из этих четырех углов прямой,
то и все четыре угла прямые.
О п р е д е л е н и е . Дее прямые, образующие при пересечении
прямые углы, называются взаимно перпендикулярными.
Т е о р е м а 4.4. Для любой точки О плоскости и любой прямой
р существует одна и только одна прямая, проходящая через О
и перпендикулярная р.
Д о к а з а т е л ь с т в о . Рассмотрим два случая.
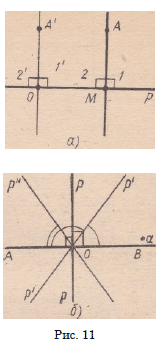
Первый случай’. О $ р.
а) С у щ е с т в о в а н и е . Пусть О* = Sp (О) и М — точка
пересечения прямых 00′ и р (рис. 10, а). При еимметрии Sp лучи
МО и МО’ отображаются друг на друга, луч MN — на себя. Поэтому
углы OMN и O’MN — смежные и конгруэнтные углы. Это
означает, что прямые 00′ и р перпендикулярны.
б) Е д и н с т в е н н о с т ь . Допустим, что через точку О

260 Конгруэнтные фигуры.

проходят два перпендикуляра к прямой
р (рис. 11,6). Тогда, как это следует из
теоремы 4.2, прямые О А и О В при симметрии
Sp отображаются на себя. Так как эти
прямые пересекаются в точке О, отсюда получаем,
что эти прямые имеют вторую общую
точку O’— Sp (О). Но через две точки
проходит единственная прямая, поэтому
(ОА) = (ОВ). Это противоречит сделанному
допущению.

Конгруэнтные фигуры 2

Второй случай1. О £ р.
а) С у щ е с т в о в а н и е . Возьмем
произвольную точку A tp. Как мы только
что показали, существует прямая AM (М £
;
няя точка) развернутого угла не единственна.