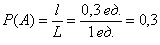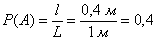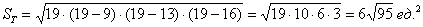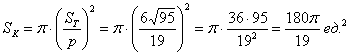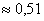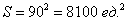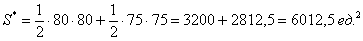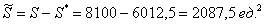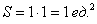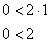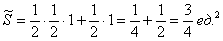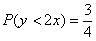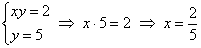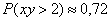Треугольник в теории вероятности (4 видео)

1.5. Геометрическое определение вероятности

Классическое определение вероятности оказывается эффективным для решения целого спектра задач, но с другой стороны, обладает и рядом ограничений. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. Простейший пример:

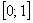
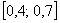
На отрезок наудачу бросается точка. Какова вероятность того, что она попадёт в промежуток ?

Поскольку на отрезке бесконечно много точек, то здесь нельзя применить формулу 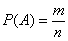(ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности:

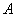
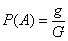
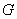
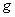
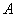
Вероятность наступления некоторого события в испытании равна отношению , где – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а – мера, выражающая количество благоприятствующих событию исходов.

На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.
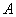
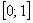
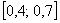
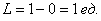
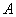
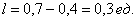
Рассмотрим событие: – брошенная на отрезок точка, попала в промежуток . Очевидно, что общее число исходов выражается длиной бОльшего отрезка: , а благоприятствующие событию исходы – длиной вложенного отрезка: По геометрическому определению вероятности:

Примечание: 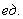– метрические единицы: метры, сантиметры или какие-то др.

Слишком просто? Как и в случае с классическим определением, это обманчивое впечатление. Обстоятельно и добросовестно разбираемся в практических примерах:

Задача 28
Метровую ленту случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.

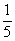
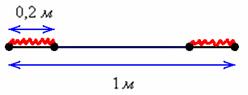
Решение: «чего тут сложного? Вероятность равна ». Это автоматическая ошибка, которую допускают по небрежности. Да, совершенно верно – длина обрезка составит не менее 80 см, если от ленты отрезать меньше 20 сантиметров. Но здесь часто забывают, что искомый разрез можно сделать как с одного конца ленты, так и с другого:

Рассмотрим событие: 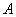– длина обрезка составит не менее 0,8 м.

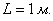
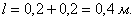
Поскольку ленту можно разрезать где угодно, то общему числу исходов соответствует её длина: Благоприятствующим исходам соответствуют участки, отмеченные красным цветом, и их суммарная длина равна:
По геометрическому определению:

Ответ: 0,4

Какой можно сделать вывод?

Даже если задача кажется вам очень простой, НЕ СПЕШИТЕ

При оформлении задач следует обязательно указывать размерность (единицы, метры, квадратные единицы, квадратные метры и т.д.). Кстати, обратите внимание, что на финальном этапе вычислений геометрическая мера сокращается. Так в рассмотренном примере, сократились метры: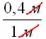
, в результате чего получилась привычная безразмерная вероятность.

Следующая задача для самостоятельного решения:

Задача 29
После бури на участке между 40-м и 70-м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что он произошёл между 50-м и 55-м километрами линии?

Значительно чаще встречаются примеры, в которых фигурируют площади:
Задача 30
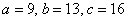
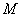
В треугольник со сторонами вписан круг. Точка произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.

Вспоминаем геометрию: вписанный круг лежит внутри треугольника и касается его сторон в трёх точках. …Представили? Отлично!

Решение: поскольку точка ставится в треугольник, а круг лежит внутри, то общему числу исходов соответствует площадь треугольника, а множеству благоприятствующих исходов – площадь вписанного круга.

Осталось вспомнить или отыскать (проще всего в Сети) школьные геометрические формулы. Если даны длины сторон треугольника, то его площадь удобно найти по формуле Герона: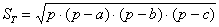
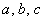
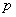
, где – длины сторон треугольника, а – полупериметр.

Сначала вычислим полупериметр треугольника: 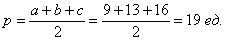, а затем его площадь:

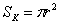
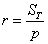
Площадь круга найдём по известной формуле . Если круг вписан в треугольник, то его радиус можно рассчитать по формуле , этого я не вообще не знал – только что нашёл в Интернете.

Итак, площадь вписанного круга:

По геометрическому определению:
– вероятность того, что точка попадёт во вписанный круг.

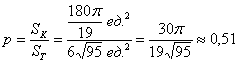
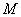
Ответ:

Более простой пример для самостоятельного решения:

Задача 31
В круге радиуса 10 см находится прямоугольный треугольник с катетами 12 и 7 см. В круг наудачу ставится точка. Найти вероятность того, что она не попадёт в данный треугольник.

Следует отметить, что в этой задаче треугольник вовсе не обязан как-то касаться окружности, он просто расположен внутри круга и всё. Будьте внимательны!

А теперь рассмотрим широко известную задачу о встрече:

Задача 32
Две грузовые машины могут подойти на погрузку в промежуток времени от 19.00 до 20.30. Погрузка первой машины длится 10 минут, второй – 15 минут. Какова вероятность того, что одной машине придется ждать окончания погрузки другой?

Решение: сначала выясним длительность временнОго промежутка, на котором могут пересечься автомобили: это 90 минут (коль скоро, от 19.00 до 20.30). Изобразим прямоугольную систему координат, где в подходящем масштабе построим квадрат размером 90 на 90 единиц: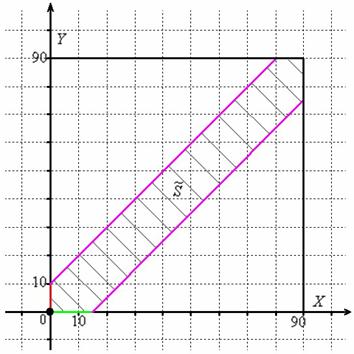

Общему множеству исходов соответствует площадь данного квадрата:

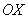
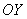
Далее по оси от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси – время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение).

Теперь из правого конца зелёного отрезка и из верхнего конца красного отрезка под углом 45 градусов проводим две линии внутри квадрата (малиновые отрезки).

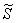
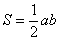
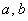
Множеству благоприятствующих исходов (когда автомобили «пересекутся» во времени) соответствует площадь заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще использовать окольный путь, а именно, вычислить площади двух прямоугольных треугольников. Используем формулу:
, где – длины катетов.

В нашей задаче: верхний треугольник имеет катеты длиной по 80 единиц, нижний треугольник – по 75 единиц. Обратите внимание, что в общем случае эти треугольники не равны.

Таким образом, суммарная площадь треугольников составляет:

И бесхитростный заключительный манёвр: из площади квадрата вычитаем площади треугольников, получая тем самым благоприятствующую площадь:

По геометрическому определению:
– вероятность того, что одной машине придется ждать окончания погрузки другой.

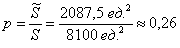
Ответ:

Подробное объяснение этого способа решения можно найти, например, в учебном пособии В.Е. Гмурмана, я же остановился лишь на техническом алгоритме, дабы не тратить ваше драгоценное время.

И если в разобранной задаче встреча явно нежелательна, то в следующей, скорее, наоборот. Романтичный эпизод для самостоятельного изучения:

Задача 33
Студенты случайным образом приходят в столовую с 14.00 до 15.00, при этом обед каждого из них занимает примерно 20 минут. Найти вероятность того, что: а) Коля встретится с Олей во время обеда, б) данная встреча не состоится.

Не нужно печалиться по поводу пункта «бэ» – любовь приходит и уходит, а кушать хочется всегда! =)

Решение, чертёж и ответ в конце книги.

Оставшиеся примеры параграфа посвящены не менее распространённому типу задач, где фигурируют неравенства.

Для начала разогревающий пример:

Задача 34
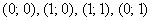
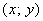
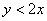
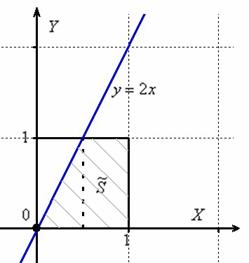
В квадрат с вершинами наудачу брошена точка . Найдите вероятность того, что координаты этой точки удовлетворяют неравенству.

Решение: изобразим на чертеже искомый квадрат и прямую :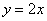

Общему множеству исходов соответствует площадь квадрата

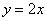
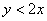
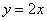
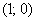
Прямая делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию ? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой , например, точку и подставить её координаты в неравенство:

Получено верное неравенство, значит, множеству благоприятствующих исходов соответствует площадь 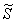трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника (разделены на чертеже пунктиром):

По геометрическому определению:
– вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству.

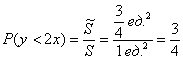
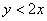
Ответ:

…аналитическую геометрию немного вспомнили, теперь на очереди математический анализ, ибо неравенства бывают не только линейными:

Задача 35
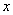
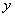
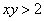
Загадываются два числа и в промежутке от 0 до 5. Какова вероятность, что ?

Схема решения уже знакома: коль скоро загадываются 2 произвольных числа от нуля до пяти (они могут быть и иррациональными), то общему количеству исходов соответствует площадь квадрата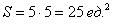
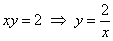
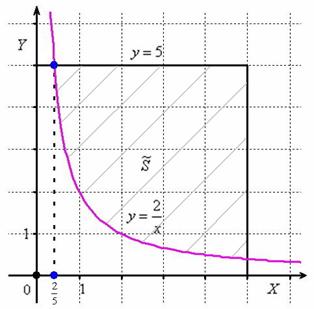
Изобразим ветвь гиперболы , которая делит квадрат на две части:

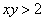
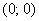
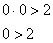
Теперь выясним, какой из этих двух «кусков» удовлетворяет неравенству . Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять , и подставим её координаты в наше неравенство:

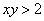
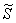
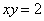
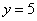
Получено неверное неравенство, а значит, условию соответствует «верхний кусок», площадь которого, деваться тут некуда, придётся вычислить с помощью определённого интеграла. Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы и прямой ):

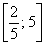
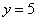
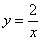
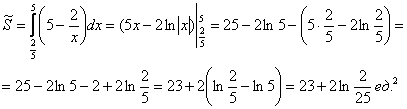
На отрезке прямая расположена не ниже гиперболы , по соответствующей формуле:

По геометрическому определению:
– вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.

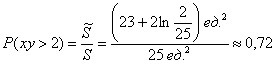
Ответ:

Аналогичный пример для самостоятельного решения:

Задача 36
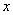
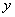
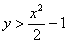
Загадываются два числа и в промежутке от 0 до 10. Какова вероятность, что ?
Данная задача (как, собственно, и предыдущая) допускает несколько способов расчёта площади, подумайте, какой путь более рационален.

В заключение следует отметить, что геометрическое определение вероятности тоже обладает своими недостатками. Один из них заключается в своеобразном парадоксе, давайте вспомним самый первый пример с отрезком 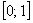, на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает.

Полную и свежую версию этой книги в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Содержание

Теория вероятности
Треугольник Паскаля vs цепочек типа «000…/111…» в бинарных рядах и нейронных сетях
Серия «Белый шум рисует черный квадрат»
🎦 Видео

Видео:Треугольник ПаскаляСкачать

Теория вероятности

С 1650 года Паскаль с трудом передвигается, так как был поражен частичным параличом. Врачи считали, что его болезнь связана с нервами и ему необходимо встряхнуться. Паскаль стал посещать игорные дома и одно из заведений имело название «Папе-Рояль», которым владел герцог Орлеанский.

В этом казино судьба свела Паскаля с шевалье де Мере, который обладал необычными математическими способностями. Он поведал Паскалю, что при бросании кости в подряд 4 раза, выпадение 6 составляет более 50%. Мере делая небольшие ставки в игре выигрывал, используя свою систему. Такая система работала, только при бросании одной кости. При переходе на другой стол, где производился бросок пары костей, система Мере не приносила прибыль, а наоборот только убытки.

Такой подход натолкнул Паскаля на мысль, в которой он захотел рассчитать вероятность с математической точностью. Это был настоящий вызов судьбе. Паскаль решил решить данную задачу при помощи математического треугольника, который был известен даже в древности (например, Омар Хайям упоминал о нем), который потом получил название — треугольник Паскаля. Эта пирамида, состоящая из чисел, каждое из которых равно суме пары чисел расположенных над ним.

Такой треугольник позволяет точно рассчитать вероятность выпадения в игре «орел-решка». Если мы подбрасываем монетку один раз, то результат вероятности мы видим во второй горизонтальной строке — одно выпадение «решка» и одно «Орел» (50/50). Также можно рассматривать варианты 2, 3, 4 бросков и т.д.

Данное изобретение было революционным. Оказывается удачу можно предсказать. По теории Паскаля неудачи можно не опасаться, если теория ее вероятности существенно мала. Такую вероятность можно легко рассчитать по статистическим данным.Открытие Паскаля используют экономисты различных стран мира. Его теорию применяют в страховых компаниях и торговых биржах.А известно ли вам, что Паскаль подал идею создания современной рулетки для казино. Он предложил сначала рассчитывать вероятность выигрыша игры в лото из 36 билетов.

Видео:Геометрическая вероятность. С какой вероятностью можно составить треугольникСкачать

Треугольник Паскаля vs цепочек типа «000…/111…» в бинарных рядах и нейронных сетях

Серия «Белый шум рисует черный квадрат»

История цикла этих публикаций начинается с того, что в книге Г.Секей «Парадоксы в теории вероятностей и математической статистике» (стр.43), было обнаружено следующее утверждение:

Рис. 1.

По анализу комментарий к первым публикациям (часть 1, часть 2) и последующими рассуждениями созрела идея представить эту теорему в более наглядном виде.

Большинству из участников сообщества знаком треугольник Паскаля, как следствие биноминального распределения вероятностей и многие сопутствующие законы. Для понимания механизма образования треугольника Паскаля развернем его детальнее, с развертыванием потоков его образования. В треугольнике Паскаля узлы формируются по соотношению 0 и 1, рисунок ниже.

Рис. 2.

Для понимания теоремы Эрдёша-Реньи составим аналогичную модель, но узлы будут формироваться из значений, в которых присутствуют наибольшие цепочки, состоящие последовательно из одинаковых значений. Кластеризации будет проводиться по следующему правилу: цепочки 01/10, к кластеру «1»; цепочки 00/11, к кластеру «2»; цепочки 000/111, к кластеру «3» и т.д. При этом разобьём пирамиду на две симметричные составляющие рисунок 3.

Рис. 3.

Первое что бросается в глаза это то, что все перемещения происходят из более низкого кластера в более высокий и наоборот быть не может. Это естественно, так как если цепочка размера j сложилась, то она уже не может исчезнуть.

Определяя алгоритм концентрации чисел, удалось получить следующую рекуррентную формулу, механизм которой показан на рисунках 4-6.

Обозначим элементы, в которые концентрируются числа J. Где n количество знаков в числе (количество бит), а длину максимальной цепочки — m. И каждый элемент получит индекс n;mJ.
Обозначим что количество перешедших элементов из n;mJ в n+1;m+1J, n;mjn+1;m+1.

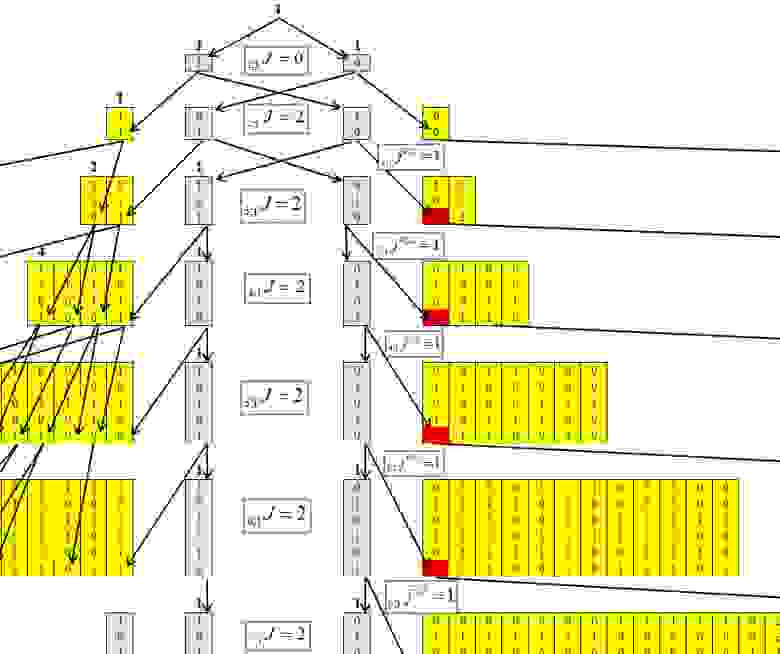
Рис. 4.

По рисунку 4 видно, что для первого кластера определить значения каждой строки не составляет трудности. И эта зависимость равна:

Рис. 5.

Определяем для второго кластера, с длиной цепочки m=2, рисунок 6.

Рис. 6.

По рисунку 6 видно, что для второго кластера зависимость равна:

Рис. 7.

Определяем для третьего кластера, с длиной цепочки m=3, рисунок 8.

Рис. 8.

Рис. 9.

Общая формула каждого элемента принимает вид:

Рис. 10.

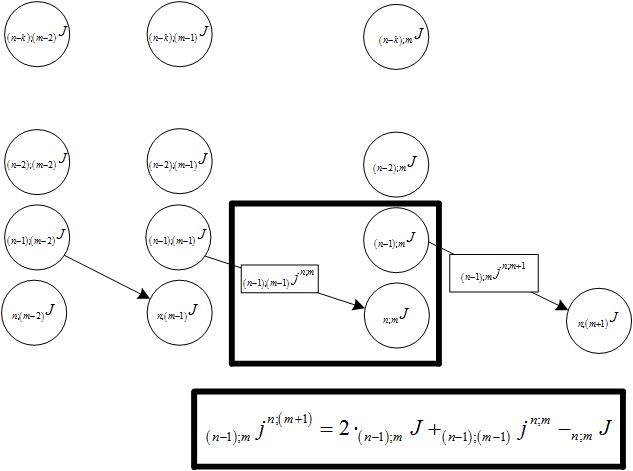
Рис. 11.

Для проверки используем свойство данной последовательности, которое показано на рисунке 12. Оно заключается в том, что последние члены строки с определенного положения принимают единственное значение для всех строк с увеличением длины строки.

Рис. 12.

Это свойство связано с тем, что при длине цепочки более чем половина всего ряда, то возможна только одна такая цепочка. Покажем это на схеме рисунка 13.

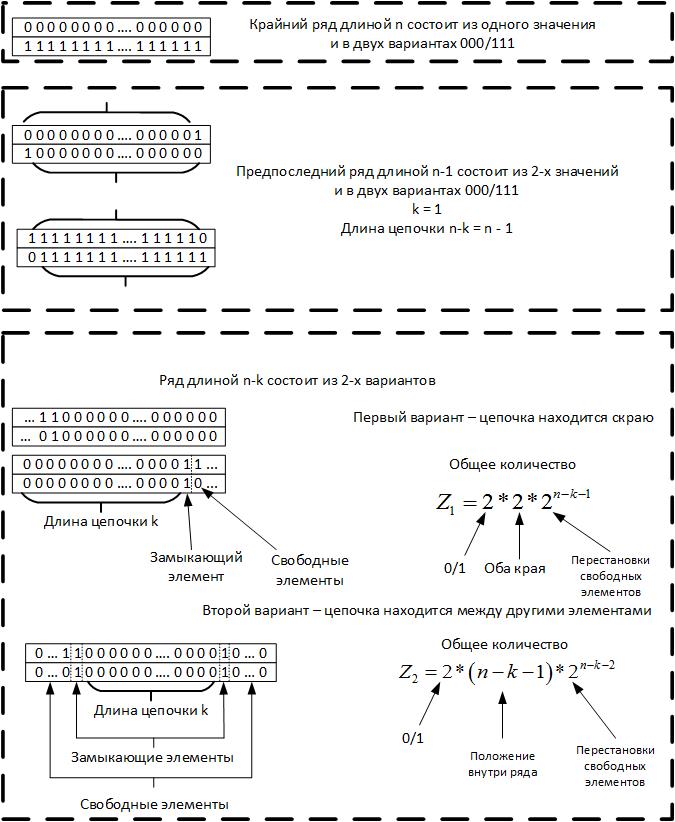
Рис. 13.

Соответственно для значений k N, то случайный процесс имеет размерность выше, чем имеющиеся данные, либо мы неверно определили уравнение целевой функции.

Тогда для первого случая проектируем нейронную сеть с 2^m сенсорами, предполагаю, что можно добавить по паре сенсоров, чтобы уловить переходы, и проводим обучение этой сети на исторических данных. Если сеть в результате обучения не сможет обучиться и будет выдавать правильный результат с вероятностью 50%, то это означает, что найденная целевая функция оптимальна и улучшить ее невозможно. Если сеть сможет обучиться, то проводим дальнейшее улучшение аналитической зависимости.

В случае если размерность ряда больше размерности случайной величины, то можно использовать свойство фрактальности случайной величины, так как любой ряд размера m содержит в себе все подпространства низших размерностей. Предполагаю, что в этом случае имеет смысл обучение нейронной сети проводить на всех данных, кроме цепочек m.

Другим подходом при проектировании нейронных сетей может быть прогнозный период.

В заключении необходимо сказать, что по дороге к этой публикации было обнаружено множество аспектов, где величина размерности случайной величины и обнаруженные свойства ее, пересекались с другими задачами при анализе данных. Но пока это все в очень сыром виде и оставим для будущих публикаций.