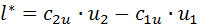Треугольник скоростей рабочего колеса (3 видео)

Лекция 2. «Движение жидкости внутри рабочего колеса центробежного насоса (треугольники скоростей на входе и выходе из рабочего колеса)»

Тема 5

«Движение жидкости внутри рабочего колеса центробежного насоса (треугольники скоростей на входе и выходе из рабочего колеса)»

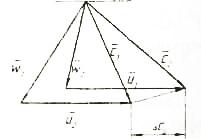
Преобразование подводимой к насосу механической энергии в энергию движущейся жидкости в лопастных насосах производится за счет непосредственного силового воздействия лопастей рабочего колеса на жидкость, заполняющую его каналы. Рабочее колесо является основным элементом насоса, а кинематические показатели (значения и направление скоростей, траектория движения и т.п.) движущейся через колесо жидкости оказывают решающее влияние на энергетические параметры колеса (напор, подача, КПД).

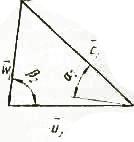
Жидкость, проходя через колесо, совершает сложное движение: она входит в колесо в направлении, параллельном оси вала, а выходит перпендикулярно оси. При этом каждая частица жидкости вращается вместе с колесом с окружной скоростью υ и одновременно перемещается вдоль лопатки с относительной скоростью ω. Согласно общим положениям механики жидкости, абсолютная скорость υ в области лопастного колеса может быть получена как геометрическая сумма относительной ω и переносной u скоростей. В векторной форме: υ=ω+ū

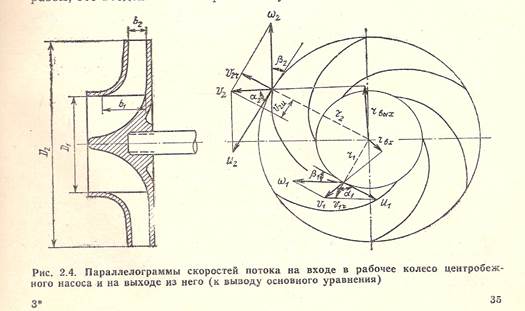
Параллелограмм скоростей потока в рабочем колесе центробежного насоса.

В основу представления об установившемся движении потока через рабочее колесо центробежного насоса положена гипотеза о струйном течении жидкости. Согласно этой гипотезе траектория каждой частицы жидкости в пределах межлопастного канала колеса по форме совпадает с кривой очертания лопасти.

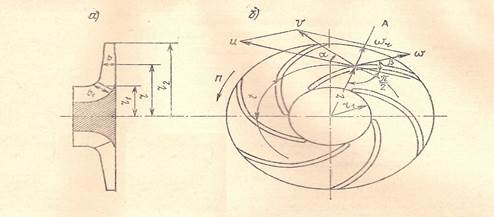
Предположим, что заданы геометрические размеры рабочего колеса центробежного насоса (рис. а), его объемная подача Q и частота вращения n. Определим, пользуясь гипотезой о струйном течении, значения и направления относительной скорости на плоском сечении колеса, перпендикулярном оси насоса в некоторой точке потока, отстоящей от оси вращения на расстоянии r (рис. б). Для определения значения относительной скорости воспользуемся уравнением неразрывности, составив его для цилиндрического сечения потока, проходящего через рассматриваемую точку. Площадь этого сечения обозначим через f_r. Радиальная составляющая скорости потока

Учитывая коэффициентом ψ стеснение сечения телом лопастей шириной b, получим:

Переносная скорость в рассматриваемой точке потока равна окружности скорости вращения колеса

и направлена по касательной к окружности радиусом r в сторону вращения.

Радиальная составляющая относительной скорости ω_r перпендикулярна вектору переносной скорости u. Касательная к поверхности лопасти, по которой направлена относительная скорость ω образует угол β с направлением обратным переносной скорости. Проведя из конца вектора ω_r прямую, параллельную направлению скорости u, до пересечения с этой касательной, получим, согласно плану скоростей, в этой точке пересечения конец вектора относительной скорости ω. Значение относительной скорости:

ω= ω_r/sin β =Q/(2πrbψ sin β)

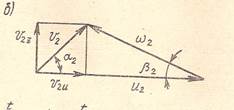
Суммируя по правилу параллелограмма относительную и переносную скорость, получим полную скорость. Поскольку радиальная составляющая ω_r относительной скорости равна радиальной составляющей υ_r абсолютной скорости, то значение скорости υ может быть определена из соотношения:

где α – угол между направлениями абсолютной и переносной скоростей.

Таким образом, гипотеза о струйном течении жидкости, основанная на предположении о бесконечном числе лопастей, позволяет построить параллелограмм скоростей в любой точке внутри рабочего колеса насоса.

Коэффициент стеснения ψ равен отношению действительной площади сечения потока к площади сечения свободного от лопастей:

ψ=(2πrb – zbs)/ 2πrb

где z – число лопастей, s – толщина лопастей в рассматриваемом цилиндрическом сечении.

Обозначая через t=2πr/z шаг, расстояние по окружности между одноименными точками смежных лопастей, получим, что коэффициент стеснения

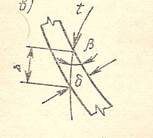
Толщина лопасти s может быть выражена через нормальную толщину δ и угол β

Величина окружной составляющей абсолютной скорости u жидкости характеризует закрутку жидкости на входе в рабочее колесо u₁ и на выходе u₂. На входе в рабочее колесо закрутка жидкости может отсутствовать u₁=0 или u₁≠0, при этом она направлена в сторону вращения (положительная) и против вращения (отрицательная). Закрутка потока применяется с целью улучшения антикавитационных свойств насоса. Закрутка в сторону вращения рабочего колеса способствует увеличению всасывания жидкости насосом, против вращения насоса – увеличение напора.

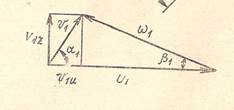
Построим треугольники скоростей на входе и выходе в рабочем колесе насоса.

При построении треугольников скоростей осевых насосов следует учитываьб две особенности:

1) Скорости переносного движения всех точек лопастей рабочего колеса в том числе входной и выходной кромок для рассматриваемого цилиндрического слоя, определяя по формуле: u=u₁= u₂=2πr_in/60

2) В силу сплошности потока осевые составляющие абсолютной скорости υ во всех точках рассматриваемого цилиндрического слоя должна быть:

где D – внешний диаметр рабочего колеса, d_вт – диаметр втулки.

Таким образом, треугольники скоростей на входной и выходной кромках лопастей имеют одинаковое основание и равную высоту.

Принципиальное отличие работы решетки профилей от единичного профиля заключается в том, что направления скорости жидкости до и после решетки различны, т.к. решетка профилей меняет направление скорости на бесконечности, а единичный профиль этого направления не меняется.

Тема 6

«Основное уравнение насоса (уравнение Эйлера)»

Напор, развиваемый насосом, и коэффициент полезного действия тесно связан со значением и направлением скоростей потока жидкости в межлопастных каналах колеса. Для установления этой связи воспользуемся классической теоремой об изменении моментов количества движения, которая может быть сформирована следующим образом: производная по времени главного момента количества движения системы материальных точек относительно некоторой оси равна сумме моментов всех внешних сил, действующих на эту систему. Математически теорема записывается следующим образом:

где m – масса рассматриваемой системы материальных точек;

υ – абсолютная скорость их движения;

r – расстояние до оси.

Удобство теоремы об изменении моментов количества движения в приложении к сплошной среде заключается в том, что с ее помощью динамическое взаимодействие между жидкостью и обтекаемыми поверхностями можно определить по характеру течения в контрольных сечениях без учета структуры потока внутри выделенного объема.

При подаче насоса Q масса жидкости, участвующей в движении, составляет: m = ρQ, где ρ – плотность жидкости.

Момент количества движения на выходе из колеса:

Момент количества движения жидкости на входе в колесо

С учетом сделанных допущений это уравнение может быть переписано в виде:

Из треугольников скоростей следует, что

где D₁ – диаметр всаса, D₂ – диаметр рабочего колеса.

Нарисуем параллелограммы скоростей потока на входе в рабочее колесо центробежного насоса и на выходе из него.

Подставляя значение r_вых и r_вх , получим:

Все внешние силы, действующие на массу жидкости, заполняющей межлопастные каналы рабочего колеса, можно разделить на три группы:

2) Давление на жидкость.

3) Силы на обтекаемых поверхностях рабочего колеса.

Таким образом, момент всех внешних сил относительно оси вращения сводятся к моменту динамического воздействия рабочего колеса M_р.к. на протекающую через него жидкость, т.е.

При этом, мощность, передаваемая жидкости рабочим колесом насоса, равна произведению M_р.к. ω = ρgQH_т

где H_т – теоретический напор, создаваемый рабочим колесом насоса.

Эта зависимость была впервые выведена в середине 18 века математиком и механиком Леонардом Эйлером, членом Петербургской академии. Она получила название уравнение Эйлера или основное уравнение лопастного насоса.

Тема 7

«Законы подобия применительно к центробежным насосам»

Геометрическое подобие в гидромеханике означает подобие всех поверхностей, ограничивающих и направляющих поток. При моделировании гидравлических машин два насоса могут быть названы подобными, если все линейные размеры одного из них (модель) в одинаковое число раз меньше или больше соответствующих размеров другого (натура). Математически гидравлическое подобие сравниваемых насосов определяется посредством линейного коэффициента подобия:

где D_н, b_н, и D_м, b_м – соответственно диаметры и высоты рабочих колес модельного и натурного насосов.

Геометрическое подобие означает также постоянство отношений любых других размеров у модели и натуры:

Кинетическое подобие означает, что безразмерные поля скоростей в рассматриваемых потоках должны быть одинаковы, т.е. отношения скоростей всех соответствующих частиц жидкости, участвующих в движении, должны быть равны между собой, а траектории движения в сравниваемых гидравлических системах – геометрически подобны.

Математически условия кинематического подобия могут быть выражены в виде ряда отношений

Динамическое подобие кроме соблюдения условий геометрического и кинематического подобия означает пропорциональность сил, действующих в соответствующих точках потока.

В практике моделирование гидравлических машин очень большое значение имеет критерий подобия Эйлера. Он может быть выражен следующим образом:

E_u = p / ρυ 2 = gH / υ 2

Принимаемые в условии расход Q, напор Н и диаметр рабочего колеса D. Условие подобия может быть записано в виде:

Уравнение устанавливает зависимость между основными энергетическими параметрами (подача, напор) модельного и натурного насосов.

Тема 8

Одни и те же значения подачи и напора могут быть получены в насосах с различной частотой вращения.

Коэффициентом быстроходности n_s насоса называется частота вращения другого насоса таких же размеров, при которых, работая в том же режиме с полезной мощностью в 1л.с., он создает напор, равный 1м.

Подставляя вместо мощности N ее значение ρgQH / 763 для насосов перекачивающих воду (ρ = 1000 кг/м 3 ) получим другую формулу для определения коэффициента быстроходности (или частота вращения рабочего колеса):

Тема 9

«Кавитация насосов. Высота всасывания центробежного насоса»

Кавитация представляет собой процесс нарушения сплошного потока жидкости, происходящий там, где местное давление, понижаясь, достигает некоторой критической величины. Процесс сопровождается образованием пузырьков, насыщенных паром жидкости, а также воздухом, выделяющемся из жидкости. Поэтому данный процесс отождествляется с кипением. При большом количестве в жидкости растворенного воздуха уменьшение давления приводит к выделению из нее воздуха и образованию газовых полостей (каверн), в которых давление выше, чем давление насыщенных паров жидкости.

Разрушение или «захлопывание» кавитационных пузырей при переносе их потоком в область с давление выше критического происходит очень быстро и сопровождается своего рода гидравлическими ударами. Наложение большого числа таких ударов приводит к появлению характерного шипящего звука, который всегда сопутствует кавитации. В подавляющем большинстве случаев кавитация сопровождается разрушением поверхности, но которой возникают кавитационные пузыри. Это разрушение является одним из самых опасных последствий кавитации, называется кавитационной энергией. Механические повреждения рабочих органов гидравлических машин в результате кавитационной эрозии за относительно короткий срок могут достигнуть размеров, затрудняющих их нормальную эксплуатацию и даже ее практически невозможной.

Высота всасывания насосов.

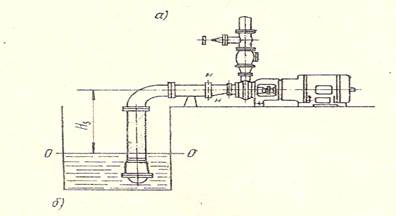
Рассмотрим три основные схемы установки центробежных насосов по отношению к уровню свободной поверхности жидкости в приемном резервуаре.

Схема 1. Уровень свободной поверхности расположен ниже оси рабочего колеса насоса.

Давление на входе в насос определяется величиной:

где H_s – геометрическая высота всасывания (разность отметок оси рабочего колеса и свободной поверхности жидкости в резервуаре);

P_атм – атмосферное давление;

P_н – давление во всасывающем трубопроводе;

υ 2 _н – скорость движения жидкости во всасывающем трубопроводе;

ω_o_-н – потери напора во всасывающей линии насоса, м (или сумма потерь на входе, потерь на трение по длине трубопровода, местные сопротивления).

Величина вакуума на входном сечении определяют по формуле:

H_в – вакуумметрическая высота всасывания.

Зависимость между высотой всасывания и вакуумметрической определяется уравнением:

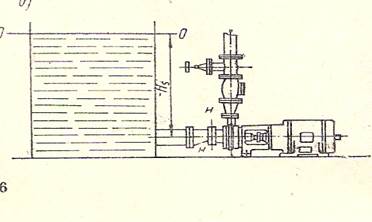
Схема 2. Уровень свободной поверхности расположен выше оси рабочего колеса насоса.

Величина значения H_s будет отрицательной. Отрицательное значение геометрической высоты всасывания называется подпором.

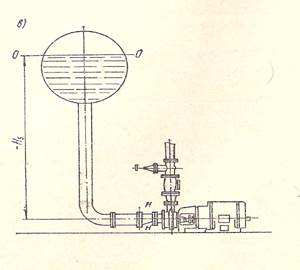
Схема 3. Откачка жидкости из замкнутого резервуара. Принципиальное отличие данной схемы работы насоса от рассматриваемой ранее схемы 2 заключается в вакуумметрической высоте всасывания.

Р_изб – избыточное давление. Оно может быть положительным, отрицательным и зависит от технологического назначения насоса и конструктивных особенностей.

Дата добавления: 2015-07-10 ; просмотров: 4077 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Движение жидкости в рабочем колесеСкачать

Треугольники скоростей осевых компрессоров

В соответствии с основным уравнением турбомашин (уравнением Леонарда Эйлера) работа, переданная лопатками рабочего колеса единице протекающей массы, определяется выражением

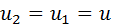
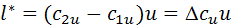
или для осевых машин с движением по цилиндрическим поверхностям тока, когда , как

Таким образом, энергообмен в рабочем колесе определяется кинематикой потока, а именно величиной окружной скорости решетки и изменением окружной составляющей абсолютной скорости потока от входа в колесо до выхода из него. Поэтому ясное представление о форме движения в рабочем колесе чрезвычайно важно для понимания основных особенностей работы турбомашин, в частности компрессоров.

Форма течения в области рабочего колеса определяется скоростями абсолютного движения (обозначаемыми в дальнейшем с), построенными в неподвижной системе координат (системе, связанной с корпусом машины), переносного движения (u) — движения лопаток рабочего колеса и относительного движения (w), то есть движения среды относительно движущихся с окружной скоростью лопаток рабочего колеса. Скорость относительного движения — это скорость среды в системе координат, связанной с вращающимися лопатками рабочего колеса.

Основной связью, определяющей соотношения между абсолютными, переносными и относительными скоростями, является условие сложения векторов 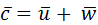, утверждающее, что вектор абсолютной скорости является суммой векторов скоростей переносной и относительной. Графическое изображение условия называется треугольником скоростей, который может быть построен как для входа в рабочее колесо, то есть для течения перед рабочим колесом, так и для выхода из рабочего колеса.

Совмещенные треугольники скоростей для входа и выхода называются иногда планами скоростей, они характеризуют кинематику потока в рабочем колесе, в конечном счете определяющую и величину переданной работы.

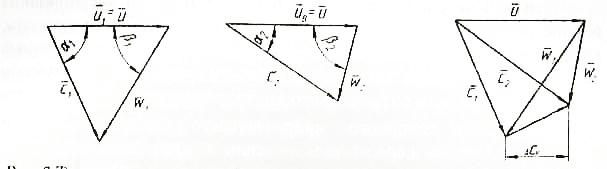
В современной практике проектирования и расчета турбомашин в основном используются два метода совмещения треугольников при построении планов скоростей. В компрессоро- и турбостроении план скоростей обычно строится при совмещении началам векторов абсолютных и относительных скоростей для треугольников входа и выхода (рис. 1).

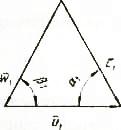
Рис.1. Треугольники скоростей при совмещении начала их векторов

В вентиляторостроении при анализе режимов работы осевых ступеней с течением по цилиндрическим поверхностям тока (когда 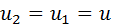) планы скоростей строят совмещением векторов окружных скоростей (рис.2).

Очевидно, оба момента построения планов скоростей допустимы и поэтому необходимо всегда уметь перейти от одной формы плана скоростей к другой.

Вполне естественно, что треугольники скоростей, т.е. план скоростей, отражающих картину течения, определяются как неподвижными, так и подвижными лопатками и, прежде всего, их геометрической формой.

Рис. 2 Треугольники скоростей при совмещении векторов окружных скоростей

Действительно, проследим, за потоком от входа в ступень осевого компрессора до выхода из него. Предположим, что перед решеткой входного направляющего аппарата среда движется в осевом направлении, то есть вдоль оси машины. Решетка направляющего аппарата в этом случае разместится поперек движущегося потока. Если мы будем рассматривать течение на какой-либо цилиндрической поверхности, соосной с осью ступени, то, развернув такую поверхность на плоскость, получим картину, изображенную на рис. 3.

Рис. 3 Схема входа потока в направляющий аппарат

Рис.4. Схема обеспечения заданного

направления потока на выходе из решетки пластин

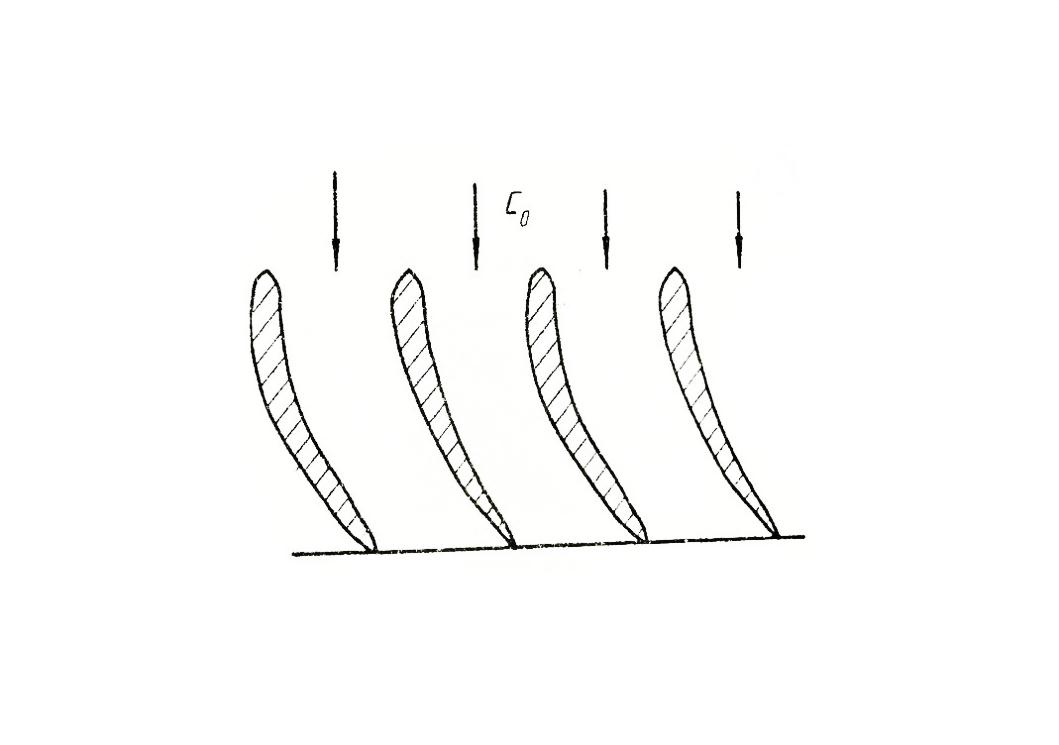
Так как направление векторов с₀ определяется особенностями течения где-то впереди рассматриваемой ступени и является заданным, то конструктор, проектируя ступень и стремясь уменьшить потери при обтекании лопаток, очевидно, должен придать входным элементам лопаток неподвижной решетки направление, примерно соответствующее вектору абсолютной скорости с₀, набегающего на лопатки потока.

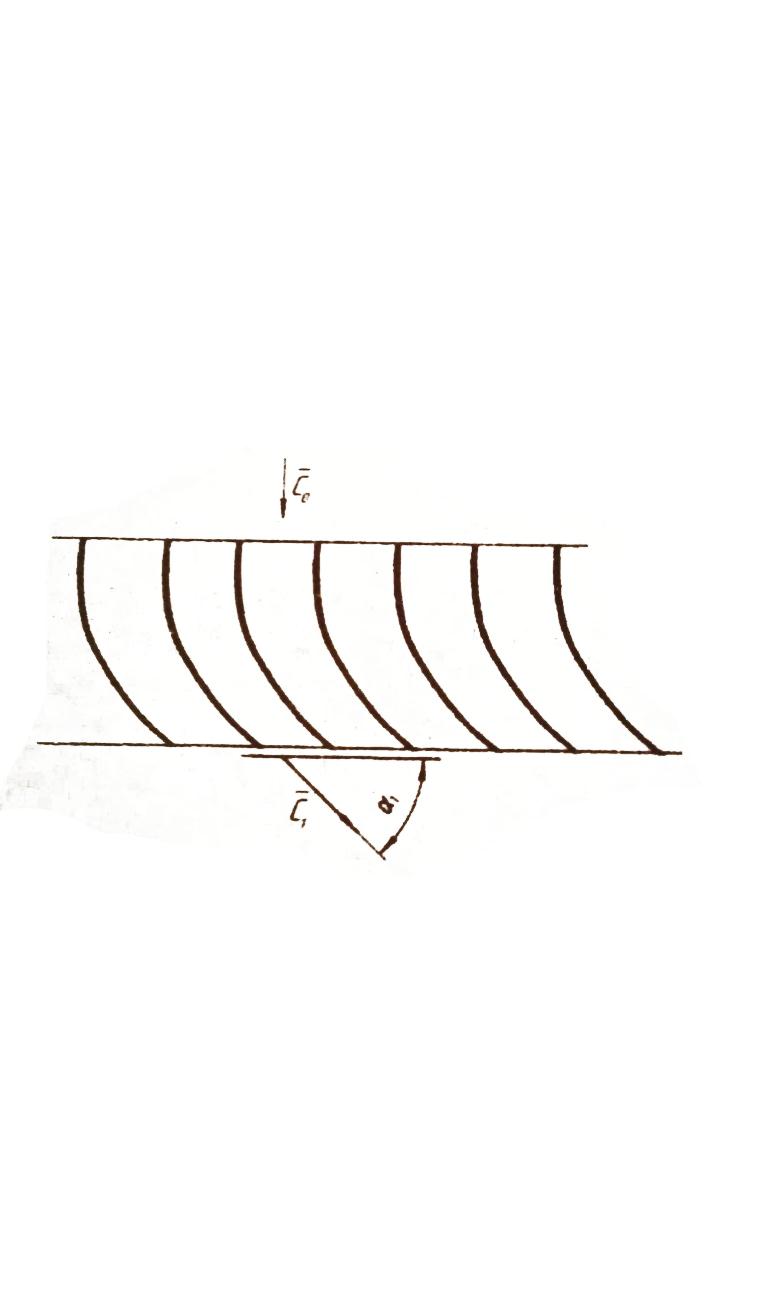
Входной направляющий аппарат (ВНА) ставится для придания вполне определенного направления потоку перед рабочим колесом, выбираемого при проектировании наиболее выгодной для заданных условий ступени. Если направление скорости перед рабочим колесом задано вектором с₁,то очевидно, что это направление должны придать потоку лопатки входного направляющего аппарата. Вполне естественно, что в первом приближении направление потока на выходе из решетки определится направлением выходных кромок лопаток, что становится совершенно очевидным при предельном переходе к решетке из бесконечно тонких пластин, очень близко расположенных друг к другу (рис. 4).

В реальных решетках действительное направление скорости отличается от направления выходных кромок лопаток втем большей степени, чем больше расстояние между лопатками. На направление скорости выхода влияют и другие геометрические характеристики решетки, а также режимы обтекания (числа М и Re, углы набегания потока на лопатки и т.д.).

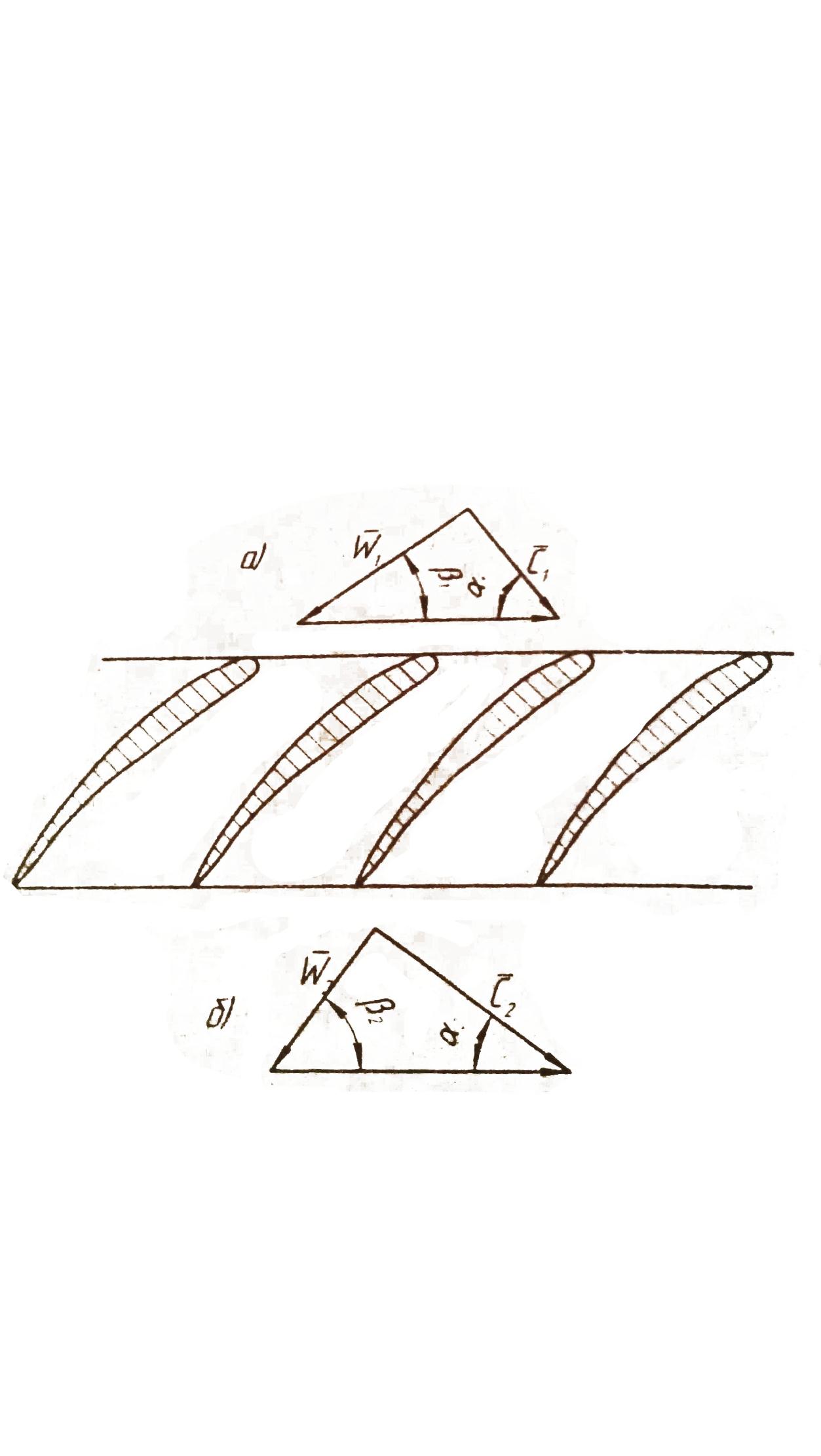
Рис. 5. Треугольники на входе и выходе рабочего колеса осевого компрессора

Если перед рабочим колесом течение определяется вектором с₁ (скоростью выхода среды из входного направляющего аппарата), то на перемещающиеся лопатки рабочего колеса поток набегает со скоростью и, следовательно, треугольник скоростей перед лопатками рабочего колеса имеет вид, изображенный на рис. 5а.

Профилируя лопатки рабочего колеса, конструктор, стремясь уменьшить потери при набегании потока на лопатки, придает их входным кромкам направление, совпадающее с направлением набегающего потока, то есть с направлением скорости w₁.

Выбрав кривизну лопаток (то есть форму и направление выходных кромок), конструктор определяет и направление относительной скорости на выходе из рабочего колеса, а следовательно, и форму треугольника скоростей на выходе из рабочего колеса (рис. 5б). Совмещение треугольников скоростей рабочего колеса даёт совмещенный план скоростей при неравенстве расходных составляющих скоростей с₁_z 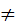с₂_zперед и за рабочим колесом. При равенстве расходных составляющих скоростей с_1z = с_2z построение треугольников скоростей упрощается (рис.7).

Видео:Турбинная ступень. Треугольники скоростейСкачать

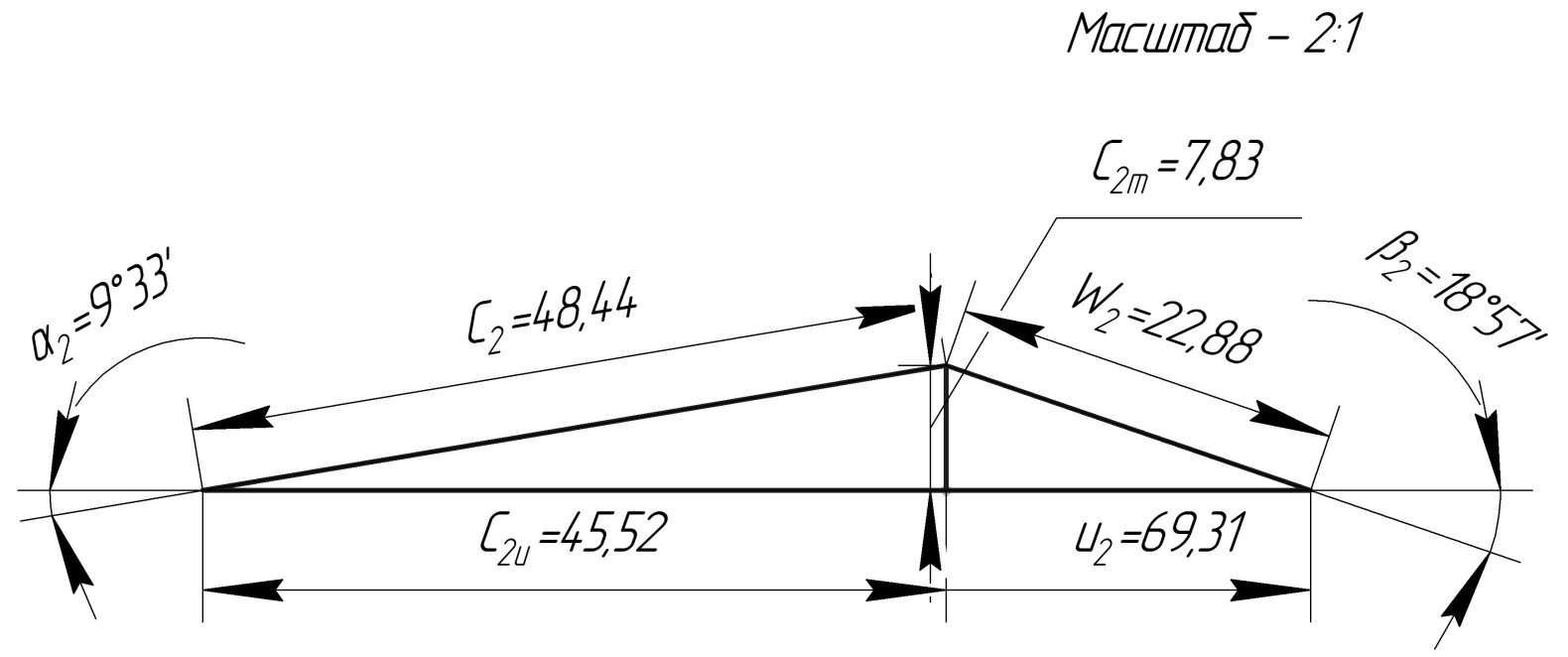
Треугольник скоростей на выходе

Для построения треугольника скоростей на выходе используем полученные в расчете величины U₂_m, C₂_m, β₂.

Относительная скорость на выходе:

м/с.

Абсолютная скорость перед выходом из рабочего колеса и угол α₂:

м/с.

Абсолютная скорость после выхода из рабочего колеса и угол α₃:

м/с

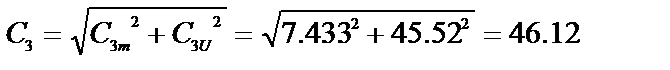
Треугольник скоростей на выходе показан на рис. 2.

Параметры номинального режима

Гидравлический, объемный КПД определены раньше.

КПД насоса на номинальном режиме:

Мощность, потребляемая насосом:

кВт

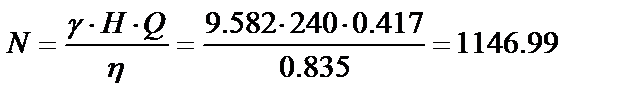
7. Расчёт характеристик насоса

Для расчёта характеристик насоса используем относительные характеристики, номера кривых выбираем по значению и считаем значения -для подачи равными от :

8. Разгрузка насоса от гидравлических сил

Осевая сила Р₁ возникает из-за наличия отличных давлений в различных частях корпуса насоса и образуется с учётом вращения жидкости в пазухах между колесом и корпусом:

34.021 кН

Осевая сила Р₂ возникает в результате изменения количества движения в осевом направлении из-за поворота потока:

кН

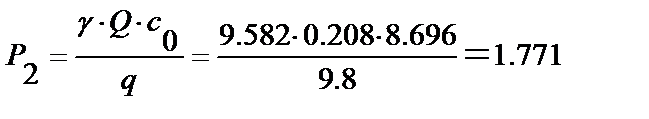
— статическая составляющая напора:

— радиус переднего уплотнения:

— суммарная осевая сила:

кН

Радиальная сила

Радиальная сила возникает на режимах работы, отличных от номинального и может быть определена по формуле:

Полный КПД насоса:

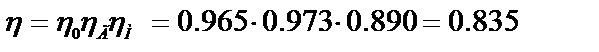
η_м = .

Графическая часть

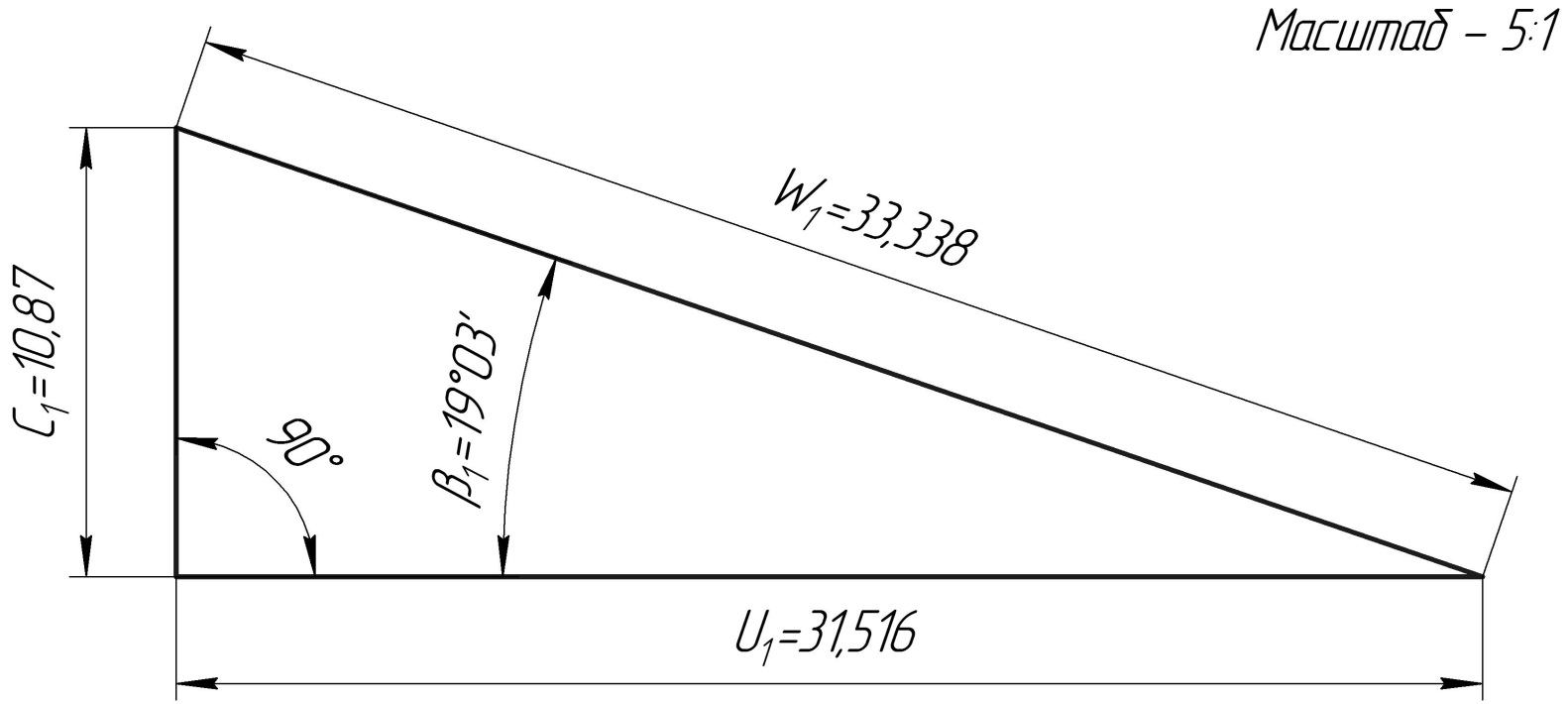
Построение треугольников скоростей на входе и выходе из рабочего колеса

Рис.1 Треугольник скоростей на входе в рабочее колесо

Рис.2 Треугольник скоростей на выходе из рабочего колеса

Построение профиля лопасти в плане колеса

Построение профиля лопатки показано на рис.3.

Рис.3 Схема построения профиля лопасти

Построение меридианного сечения рабочего колеса

Необходимо определить радиус входа в рабочее колесо, ширину входа и выхода колеса. Радиус входа в рабочее колесо:

м;

Построение эскиза меридианного сечения рабочего колеса

Эскиз сечения колеса выполняется по рассчитанным размерам с учетом рекомендаций(п.1). На рисунке показаны эпюры действия осевых сил и предполагаемый способ разгрузки от осевой силы. Построение эскиза показано на рис. 4.

Рис.4 Эскиз меридианного сечения рабочего колеса

Рис.5 Эскиз рабочего колеса
Литература

1.Насосы.Ю.Ф.Горбачёв и др.-Ч.1.-Севастополь: СВВМИУ,1886.

2.Мирошниченко С.Т.Насосы АЭС: Альбом рисунков.- Севастополь: СИЯЭиП,1998.

3. Мирошниченко С.Т.”Определение рабочих параметров центробежного насоса в составе системы, гидравлический расчёт рабочего колеса насоса”.- Севастополь: СНИЯЭиП, 2004.