Треугольник kmn равнобедренный с основанием kn прямая ab параллельна

треугольник КМN — равнобедренный с основанием KN. прямая АВ параллельна стороне MN. обоснуйте, что треугольник KAB — равнобедренный

• Рома Сайдаш
• Геометрия 2019-02-10 21:01:08 1 1

Подтверждаем подобие треугольников КАВ и КМН: угол К- общий, угол КАВ=КМН при АВМН и секущей МА(МК), угол КВА=КНМ при АВМН и секущей НВ (НК). Как следует тр-к КАВ — равнобедренный

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Геометрия, докажите что треугольник равнобедренный

треугольник KMN — равнобедренный с основанием KN . Прямая AB параллельна основанию. Докажите что треугольник AMB равнобедренный .

Все, что написано выше — чушь полнейшая. Подобие по двум углам. Первый при общей вершине, второй любой из оставшихся, попарно равные как углы при пересечении двух параллельных прямых третьей (кажись такие углы называются смежными, если склероз не обманывает)

Лирические отступления:
— Подобие «по двум общим сторонам и общему углу» — когда я учился в школе, у нас не было такого признака. Наверно перепутано с признаками сравнения треугольников.
— То, что большой треугольник является равнобедренным, никак не влияет на решение, и дополнительных построений в этой элементарной задаче проводить не надо.

Из точек A и B опустим перпендикуляры. Получим два равных треугольника. Угол K равен углу N, т. к. треугольник равнобедренный. Два перпендикуляра тоже равны между собой. Отсюда следует, что AK=BN.

ты что, не видишь .

Треугольники подобны по двум общим сторонам и общему углу. Следовательно оба равнобедренные.

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Ответы к задачам по геометрии 7 класс 682 (Часть 2)

311. В равнобедренном треугольнике ABC отрезок BD — медиана,
проведенная к основанию. Найдите периметр треугольника BDC,
если P¬ ABC = 18 см, BD = 5 см.
312. В треугольнике ABC ∠ = A C ∠ , BD — биссектриса треугольника.
Докажите, что AD = CD.
313. В треугольнике ABC отрезок CD является медианой и высотой. Докажите, что ∠ = A B ∠ .

314. На высоте MP равнобедренного треугольника KMN с основанием KN отмечена точка O (рис. 105). Докажите, что треугольник KON
равнобедренный.
315. В равнобедренном треугольнике KON с основанием KN на
продолжении биссектрисы OP отмечена точка M (рис. 105). Докажите, что треугольник KMN равнобедренный.
316. Докажите, что медианы равных треугольников, проведенные
к соответственно равным сторонам, равны.
317. Докажите, что биссектрисы равных треугольников, проведенные из вершин соответственно равных углов, равны.

318. В равнобедренном треугольнике ABC отрезок BD — биссектриса,
проведенная к основанию. Найдите ее длину, если периметр треугольника ABC равен 28 см, а периметр треугольника ABD равен 20 см.
319. Докажите, что треугольник, в котором медиана делит периметр пополам, является равнобедренным.
320. Докажите, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
321. Докажите, что в равнобедренном треугольнике биссектрисы,
проведенные из вершин при основании, равны.
322. Треугольники ABC и DBC равны (рис. 106). Докажите, что точка
пересечения отрезков AD и BC делит отрезок AD пополам.
323. Перпендикулярные отрезки AD и BC пересекаются в точ ке O, причем ∠ = ABC D∠ BC (рис. 106). Докажите, что треугольник ACD равнобедренный.

324. Докажите равенство равнобедренных треугольников по основанию
и проведенной к нему медиане.
325. Докажите равенство равнобедренных треугольников по углу,
лежащему против основания, и высоте, проведенной из вершины
этого угла.

330. Даны треугольники ABC и A B1 1C1, в которых AB = A B1 1,
BC = B C1 1, ∠ = A A ∠ 1, ∠ = B B ∠ 1. Какое из четырех данных условий
можно исключить, чтобы оставшихся условий было достаточно для доказательства равенства треугольников по первому признаку; по второму
признаку?
331. Треугольники ABC и AB1C имеют общую сторону AC, причем точки B и B1
лежат по разные стороны от прямой AC, ∠ = BAC B ∠ 1AC
∠ = BAC B ∠ 1AC. Назовите дополнительное условие, необходимое для доказательства равенства треугольников. Приведите все возможные ответы

332. В треугольниках ABC и A B1 1C1 AC = A C1 1 и BC = B C1 1. Какое
равенство необходимо добавить к условию, чтобы равенство данных треугольников можно было доказать по третьему признаку?
333. Три стороны одного треугольника соответственно равны трем сторонам другого треугольника. Равны ли углы между соответственно равными сторонами этих треугольников? Почему?
334. Верно ли, что два равносторонних треугольника равны, если они
имеют одинаковые периметры?
335. Верно ли, что два произвольных треугольника равны, если они
имеют одинаковые периметры? Является ли верным обратное утверждение?

336. Начертите равнобедренные треугольники ABC и ADC с общим
основанием AC.
а) Соедините точки B и D. Выделите цветом равные треугольники,
равенство которых можно доказать по третьему признаку.
б) Назовите углы, биссектрисы которых лежат на прямой BD.
337. Начертите равные треугольники ABC и A B1 1C1.
а) Проведите медианы BM и B M1 1.
б) Выделите цветом пары равных треугольников, образовавшихся на рисунке. Можно ли доказать их равенство по первому признаку; по второму признаку; по третьему признаку?

338. На рис. 109 AB = CD, BC = AD. Докажите равенство тре угольников ABD и CDB.
339. На рис. 110 AB = CB, AD = CD. Докажите равенство тре угольников ABD и CDB.

340. Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого
равнобедренного треугольника, то такие треугольники равны. Докажите.
341. Если две стороны и периметр одного треугольника соответственно равны двум сторонам и периметру другого треугольника,
то такие треугольники равны. Докажите.
342. На рис. 111 ¬ ¬ ABC C = DA. Докажите, что ¬ ¬ ABD C = DB.

343. Равнобедренные треугольники ABC и ADC имеют общее основание AC и лежат по одну сторону от прямой AC. Докажите, что
∠ = ADB C ∠ DB .
344. На рис. 112 AB = CD, AC = BD. Докажите равенство тре угольников ABD и DCA.
345. На рис. 113 AB = CD, BF = CE, AE = FD. Докажите, что треугольник EOF равнобедренный.
346. На рис. 112 ¬ ¬ AOB D = OC. Докажите равенство тре угольников ABC и DCB. С помощью каких признаков равенства тре угольников
его можно обосновать?
347. Отрезки AB и CD пересекаются в точке O, которая является
середино

348. Точки A, B, C и D лежат на одной прямой, причем AE AE 1 2 = , BE BE 1 2 = (рис. 114).
Докажите, что треугольники CDE1 и CDE2
равны.
349. Точки A, B, C и D лежат на одной прямой, причем AE AE 1 2 = , CE CE 1 2 =
(см. рис. 114). Докажите, что треугольники BDE1
и BDE2
равны.
350. Докажите равенство треугольников по
двум сторонам и медиане, проведенным из
одной вершины.
351. Докажите равенство равнобедренных
треугольников по боковой стороне и проведенной к ней медиане.

352. Определите, какие из приведенных утверждений верны:
а) две прямые, перпендикулярные третьей, перпендикулярны;
б) две прямые, параллельные третьей, параллельны;
в) через любую точку плоскости можно провести прямую, параллельную данной;
г) через любую точку плоскости можно провести не больше одной
прямой, параллельной данной.
353. Через точку C, не принадлежащую ни одной из прямых a и b, проведена прямая c. Определите взаимное расположение прямых b и c, если:
а) a b|| , c a|| ; б) a b ⊥ , c a ⊥ .
Изменятся ли ответы, если точка C лежит на прямой b?

354. На рис. 124 укажите угол, который вместе
с углом 4 составляет:
а) пару внутренних накрест лежащих углов;
б) пару внутренних односторонних углов;
в) пару соответственных углов.
355. По рис. 124 определите, будут ли прямые a
и b параллельными, если:
а) ∠ = 3 6 ∠ ; г) ∠ = 2 6 ∠ ;
б) ∠ = 5 8 ∠ ; д) ∠ + 3 5 ∠ = 180°;
в) ∠ = 1 7 ∠ ; е) ∠ + 2 4 ∠ = 180°.
356. По рис. 124 определите, при каких значениях n будет верным
утверждение:
а) если ∠ = 6 ∠n, то a b¬ ;
б) если ∠ + 6 1 ∠ = n 80°, то a b¬ .
357. Определите, какие из следующих утверждений верны:
а) если при пересечении двух прямых секущей образуются восемь равных углов, то прямые параллельны;
б) если при пересечении двух прямых секущей образуются четыре равных угла, то прямые параллельны;
в) сумма двух углов треугольника может быть равна 180°

358. Начертите прямые a и b и проведите секущую c.
а) Выделите на рисунке одну пару внутренних накрест лежащих
углов красным цветом, а другую пару — синим.
б) Выделите углы, соответственные с «красными» углами, красным цветом, а углы, соответственные с «синими» углами, синим
цветом.
359. Начертите угол ABC, равный 60°.
а) От луча AB отложите угол DAB, равный 120°, так, чтобы
точки C и D лежали по одну сторону от прямой AB.
б) Параллельны ли прямые AD и BC? Почему?

360. Дан треугольник ABC. Прямая l пересекает сторону AB в точ ке D, а сторону BC — в точке E. Назовите внутренние накрест лежащие, внутренние односторонние и соответственные углы при прямых AB и BC и секущей DE.
361. По данным рис. 125, а–в докажите, что a b

362. По рис. 124 определите, параллельны ли прямые a и b, если:
а) ∠ = 4 125°, ∠ = 5 125°;
б) ∠ = 5 115°, ∠ = 3 65°;
в) ∠ = 3 65°, ∠ = 7 65°.
363. На рис. 126 ¬ ¬ ABD C = DB. Докажите, что AD ¬ BC.
364. На рис. 127 ¬ ¬ AOB C = OD. Докажите, что AB ¬ CD.

367. По рис. 124 определите, параллельны
ли прямые a и b, если:
а) ∠ = 5 135°, а угол 4 втрое больше,
чем угол 3;
б) ∠ = 2 72°, а ∠ ∠ 6 8 : : = 2 3.
368. Отрезки AB и CD пересекаются в точке,
которая является их общей серединой. Докажите, что AC ¬ BD.
369. На рис. 129 AB = BC, CD = DE. Докажите, что прямые AB и DE параллельны.
370. Известно, что ¬ ¬ ABC C = DA. Назовите параллельные стороны этих треугольников и докажите их параллельность.
371. В треугольнике ABC проведена биссектриса BL. На стороне BC отмечена точка K
так, что BK = KL. Докажите параллельность
прямых AB и KL.
372. В треугольнике ABC AB = BC, ∠ = C 80°.
Прямая l пересекает стороны AB и BC в точках D и E соответственно, причем AD

375. В треугольнике ABC ∠ = A 20°, ∠ = B 80°. Из точки B проведен луч BD так, что BC — биссектриса угла ABD. Докажите, что прямые AC и BD параллельны.
376. В треугольнике ABC ∠ = A 70°, ∠ = B 40°. На луче CB отмечена точка D, не принадлежащая отрезку BC. Луч BE — биссектриса
угла ABD. Докажите, что прямые AC и BE параллельны.

379. Обязательно ли среди углов, которые образовались при пересечении двух параллельных прямых секущей, найдутся:
а) ровно четыре острых угла;
б) не больше четырех острых углов;
в) не меньше четырех тупых углов;
г) не меньше четырех равных углов?
380. При пересечении двух параллельных прямых секущей образовались два угла с градусными мерами 80°. Могут ли эти углы быть:
а) внутренними накрест лежащими;
б) внутренними односторонними;
в) соответственными?
381. Один из углов, образованных при пересечении двух параллельных прямых секущей, равен 120°. Может ли один из остальных семи
углов быть равным 50°? Почему?

382. Внутренние односторонние углы, образованные при пересечении
двух параллельных прямых секущей, равны. Под каким углом секущая пересекает данные прямые?
383. Отрезок AB — расстояние между параллельными прямыми a и b.
Под каким углом секущая AB пересекает прямые a и b?

384. Начертите параллельные прямые a и b и секущую c, не перпендикулярную им.
а) Закрасьте восемь образовавшихся углов красным или синим
цветом так, чтобы сумма любых двух углов разных цветов была
равна 180°.
б) Из точки пересечения прямых a и c проведите отрезок, который является расстоянием между параллельными прямыми a
и b. Под каким углом этот отрезок пересекает прямую b?
385. Начертите треугольник ABC.
а) Проведите прямую, параллельную стороне AC и пересекающую стороны AB и BC в точках D и E соответственно.
б) Отметьте красным цветом угол треугольника ABC, равный
углу BDE.
в) Отметьте синим цветом угол треугольника ABC, сумма которого с углом DEC равна 180°.

387. Один из углов, образованных при пересечении двух параллельных прямых секущей, равен 18°. Найдите остальные углы.
388. Угол ABC равен 62°, а угол BCD равен 118°. Могут ли прямые AB и CD:
а) быть параллельными; б) пересекаться?
Ответ обоснуйте.
389. Угол ABC равен 29°, а угол BAD равен 141°. Могут ли прямые AD и BC быть параллельными? Ответ обоснуйте.
390. На плоскости проведены прямые a, b и c, причем a b¬ , a c ⊥ .
Определите взаимное расположение прямых b и c.
391. Прямые a и b параллельны. Точки A1 и A2 лежат на прямой a, отрезки A B1 1 и A B2 2 — расстояния между прямыми a и b.
Назовите отрезки, которые являются расстояниями между прямыми A B1 1 и A B2 2. Ответ обоснуйте.

393. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если:
а) один из внутренних односторонних углов на 30° больше другого;
б) сумма двух соответственных углов равна 56°.
394. По данным рис. 137, а определите, параллельны ли прямые a и b,
если ∠ − 2 1 ∠ = 54°.
395. Угол ABC равен 72°. Из точек A и C внутри угла проведены
лучи, параллельные сторонам угла и пересекающиеся в точке D.
Найдите угол ADC

406. Может ли треугольник иметь три тупых угла; два тупых угла;
не иметь ни одного тупого угла?
407. Может ли угол при основании равнобедренного треугольника
быть тупым; прямым?
408. Может ли прямоугольный треугольник быть равнобедренным;
равносторонним?
409. Могут ли быть равными тупоугольный и прямоугольный треугольники; тупоугольный и остроугольный треугольники?
410. Даны три внешних угла треугольника при разных вершинах.
Сколько из них могут быть острыми?

411. Начертите остроугольный треугольник ABC.
а) Измерьте углы треугольника и вычислите их сумму.
б) На луче AC отметьте точку D, не принадлежащую отрез ку AC. Определите градусную меру угла BCD, используя теорему
о внешнем угле треугольника.
в) Определите вид треугольника BCD по величине углов.
412. Начертите треугольник ABC с тупым углом A.
а) Проведите высоту BD и определите вид треугольника ABD по
величине углов.
б) Измерьте угол BAD. Как связана его градусная мера с градусными мерами углов треугольника ABC?

413. Найдите неизвестный угол треугольника, если два его угла
равны:
а) 65° и 45°; б) 120° и 18°; в) 90° и 64°.
414. Найдите неизвестные углы равнобедренного треугольника, если:
а) угол при его основании равен 40°;
б) угол, противолежащий его основанию, равен 40°.
415. Найдите неизвестные углы треугольника:
а) прямоугольного, с углом 28°;
б) равнобедренного, с углом при основании 80°.
416. Докажите методом от противного, что угол при основании равнобедренного треугольника не может быть тупым.
417. Докажите методом от противного, что треугольник не может
иметь больше одного прямого угла.
418. Найдите внутренние углы треугольника, если внешние углы при
двух его вершинах равны 135° и 110°.
419. Один из внутренних углов треугольника равен 40°, а один из
внешних — 125°. Найдите остальные внутренние и внешние углы.

420. Найдите все углы треугольника, если:
а) один из них вдвое меньше второго и на 20° больше третьего;
б) их градусные меры относятся как 1 : 3 : 5.
421. Один из углов равнобедренного треугольника равен 50°. Найдите
другие углы. Сколько решений имеет задача?
422. Найдите:
а) углы треугольника, если их градусные меры относятся как
2 : 7 : 9;
б) углы равнобедренного треугольника, если один из них ра вен 100°.
423. Может ли треугольник с углом 40° быть равным треугольнику
с углом 140°? Ответ обоснуйте.

424. Треугольник с углом 120° равен треугольнику с углом 30°.
Докажите, что данные треугольники равнобедренные.
425. В равнобедренном треугольнике ABC с основанием AC проведена биссектриса AD. Найдите углы данного треугольника, если
∠ = ADC 150°.
426. Отрезок BD — биссектриса треугольника ABC. Найдите
угол A, если ∠ = C 35°, ∠ = BDC 105°.
427. В треугольнике ABC биссектрисы, проведенные из вершин A
и B, пересекаются в точке O. Найдите угол AOB, если ∠ = A 82°,
∠ = B 38°.
428. В равнобедренном треугольнике ABC биссектрисы, проведенные из вершин при основании AC, пересекаются в точке O. Найдите углы треугольника, если ∠ = AOC 140°.
429. Один из внешних углов равнобедренного треугольника ра вен 60°. Найдите внутренние углы треугольника.
430. Внешние углы треугольника относятся как 3 : 4 : 5. Найдите
внутренние углы треугольника.
431. Найдите внутренние углы треугольника, если сумма двух из
них равна 150°, а один из внешних углов равен 80°.

432. Биссектриса равнобедренного треугольника, проведенная из вершины угла при основании, равна основанию треугольника. Найдите
его углы.
433. Биссектриса равнобедренного треугольника, проведенная из
вершины угла при основании, пересекает боковую сторону под
углом, равным углу при основании. Найдите углы треуголь ника.
434. Биссектриса внешнего угла при основании равнобедренного треугольника пересекает продолжение боковой стороны. Длина отрезка
биссектрисы от начала до точки пересечения равна основанию треугольника. Найдите внутренние углы треугольника.
435. Биссектриса внешнего угла при основании равнобедренного треугольника пересекает продолжение боковой стороны под углом, равным углу при основании треугольника. Найдите углы треугольника.

436. В треугольнике ABC биссектрисы, проведенные из вершин A и C,
пересекаются в точке O. Найдите угол AOC, если ∠ = B α.
437. Биссектриса внешнего угла равнобедренного треугольника при
вершине, противолежащей основанию, параллельна основанию треугольника. Докажите.
438. Сформулируйте и докажите утверждение, обратное утверждению предыдущей задачи.

439. Известно, что ¬ ¬ ABC D = BC, причем точка C лежит на отрезке AD. Докажите, что данные треугольники прямоугольные.
440. Равнобедренные треугольники ABC и ADC имеют общее основание AC (точки B и D лежат по одну сторону от прямой AC). Докажите,
что BD ⊥ AC

441. В прямоугольном треугольнике ABC ∠ + A B∠ = ∠C. Назовите
гипотенузу треугольника.
442. В прямоугольном треугольнике DEF высота EA лежит внутри
треугольника. Назовите катеты треугольника.
443. Прямоугольный треугольник с острым углом α равен прямоугольному треугольнику с острым углом 20°. Каким может быть значение α?
444. В треугольниках ABC и A B1 1C1 ∠ = A A ∠ 1, AB = A B1 1, BC = B C1 1
BC = B C1 1. По каким признакам можно доказать равенство этих треугольников, если:
а) угол A прямой;
б) угол B прямой?
445. Могут ли неравные прямоугольные треугольники иметь две пары
соответственно равных катетов; равные гипотенузы?

446. Начертите прямоугольный треугольник ABC с гипотенузой AB.
а) Измерьте угол A и вычислите градусную меру угла B.
б) Отметьте на рисунке наименьший внешний угол треугольника. Какова его градусная мера?
в) Проведите высоты треугольника. Сколько отрезков вы провели?

447. Начертите равнобедренный треугольник ABC с основанием AC.
а) Проведите высоту BD. Выделите цветом равные треугольники
и докажите их равенство с помощью разных признаков равенства
прямоугольных треугольников.
б) Назовите высоты треугольника BCD, проведенные к катетам.

448. Найдите углы равнобедренного прямоугольного треугольника.
449. В равностороннем треугольнике ABC проведена медиана AD.
Найдите углы треугольника CAD.
450. Найдите острые углы прямоугольного треугольника, если:
а) один из этих углов в пять раз меньше другого;
б) их разность равна 10°.
451. Найдите острые углы прямоугольного треугольника, если:
а) один из его внешних углов равен 130°;
б) их градусные меры относятся как 2 : 7.
452. На рис. 154 ∠ = A C ∠ , ∠ = ADB C ∠ DB. Докажите равенство треугольников ADB и CDB.
453. На рис. 155 AD ¬ BC, ∠ = BAC D∠ = CA 90°. Докажите равенство
треугольников BAC и DCA.
454. В треугольнике ABC углы A и C острые, BD — высота треугольника. Какая из точек A, C, D лежит между двумя другими?
455. В треугольнике ABC угол C тупой, BD — высота треугольника.
Какая из точек A, C, D лежит между двумя другими?
456. В прямоугольном треугольнике ABC к гипотенузе проведена высота BH. Найдите углы треугольника ABH, если ∠ = C 25°.
457. В треугольнике ABC высота AD делит угол A на два угла, причем ∠ = BAD 38°, ∠ = CAD 42°. Найдите углы треугольника ABC.

458. В прямоугольном треугольнике ABC с гипотенузой AC ∠ = A 45°,
катет AB = 8 см. Найдите катет BC.
459. Высота равнобедренного треугольника, проведенная к боковой
стороне, образует с основанием треугольника угол 35°. Найдите углы
данного треугольника.
460. В треугольнике ABC ∠ = B 90°. Биссектриса угла A пересекает
катет BC под углом 74°. Найдите острые углы треугольника ABC.
461. Если в треугольнике две высоты равны, то этот треугольник равнобедренный. Докажите.
462. Сформулируйте и докажите утверждение, обратное утверждению предыдущей задачи.
463. В треугольнике ABC проведена высота BD. Найдите углы данного
треугольника, если ∠ = ABD 25°, ∠ = CBD 40°. Сколько решений имеет задача?
464. Биссектриса, проведенная из вершины прямого угла треугольника, пересекает гипотенузу под углом 70°. Найдите углы, которые
образует с катетами высота, проведенная к гипотенузе.
465. Докажите равенство прямоугольных треугольников по катету
и высоте, проведенной к гипотенузе.
466. Докажите равенство прямоугольных треугольников по катету
и биссектрисе, проведенной к гипотенузе.
467. В равнобедренном треугольнике KMN с основанием KN высо ты KA и NB пересекаются в точке O. Найдите углы данного треугольника, если ∠ = KON 140°.
468. В равнобедренном треугольнике ABC с основанием AC высоты AD и BE пересекаются под углом 50°. Найдите углы данного
треугольника.

469 (опорная). Медиана прямоугольного треугольника, проведенная
к гипотенузе, равна половине гипотенузы. Докажите.
470 (опорная). Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.
Докажите.

471. Угол между биссектрисой и высотой, проведенными из вершины
наибольшего угла прямоугольного треугольника, равен 22°. Найдите
острые углы треугольника.
472. Высота, проведенная из вершины при основании равнобедренного треугольника, делит пополам угол между основанием
и биссект рисой угла при основании. Найдите углы данного треугольника.
473. Один из углов прямоугольного треугольника равен 60°, а разность между гипотенузой и катетом, прилежащим к данному углу,
равна 6 см. Найдите эти стороны треугольника.
474. В треугольнике ABC ∠ = B 90°, а внешний угол при вершине C равен 120°. Найдите стороны BC и AC, если их сумма рав на 21 см.
475. В прямоугольном треугольнике катет, прилежащий к углу 30°,
равен 18 см. Найдите длину биссектрисы треугольника, проведенной
к данному катету.
476. В треугольнике ABC ∠ = C 90°. Биссектриса BE образует с катетом AC угол 60°. Найдите катет AC, если CE = 4 см.

479. Назовите:
а) наибольшую сторону треугольника DEF, если ∠ > NK MN.
480. Из одной вершины треугольника проведены медиана, биссектриса и высота, причем никакие два из этих отрезков не совпадают. Какой
из данных отрезков наименьший?
481. Определите:
а) могут ли стороны треугольника быть равными 13 см, 20 см
и 6 см;
б) может ли сторона треугольника составлять половину его периметра;
в) могут ли стороны треугольника относиться как 2 : 3 : 5;
г) может ли основание равнобедренного треугольника быть
втрое больше боковой стороны?
482. В треугольнике ABC сторона AC наименьшая. Может ли угол B
быть прямым или тупым? Ответ обоснуйте.
483. В равнобедренном треугольнике одна сторона равна 16 см, а другая — 5 см. Найдите длину основания треугольника.

484. Начертите треугольник ABC, в котором ∠ = C 100°.
а) Назовите наибольшую сторону треугольника и проверьте свой
ответ с помощью измерений.
б) Измерьте все стороны треугольника и проверьте, выполняется ли неравенство треугольника для сторон треугольника ABC.
в) Пользуясь результатами измерений, назовите наименьший
угол треугольника.
485. Начертите остроугольный треугольник ABC.
а) Измерьте углы треугольника и определите его наибольшую
и наименьшую стороны.
б) Проведите медиану BD. Запишите неравенство треугольника
для стороны BD в треугольниках ABD и CBD.

498. Периметр равнобедренного треугольника равен 70 м. Найдите
стороны треугольника, если одна из них равна 10 м.
499. Две стороны треугольника равны 1,2 м и 0,4 м. Найдите длину
третьей стороны, если она выражается целым числом метров.
500. Докажите, что медиана треугольника меньше половины его периметра.
501. Докажите, что каждая сторона треугольника меньше половины его периметра.

502. В прямоугольном треугольнике ABC отрезок CD — биссектриса,
проведенная из вершины прямого угла. Назовите наименьшую сторону
треугольника, если угол CDA тупой.
503. В прямоугольном треугольнике ABC к гипотенузе проведена высота CD. Назовите наименьший угол треугольника, если
AD ). В каких пределах может изменяться:
а) длина третьей стороны;
б) периметр треугольника?
507. Докажите, что медиана треугольника меньше полусуммы сторон,
между которыми она проходит.
508. Докажите, что сумма высот треугольника меньше его периметра.

511. Докажите равенство треугольников ABC и A B1 1C1, если:
а) AB = A B1 1, ∠ = A A ∠ = ° 1 85 , ∠ = B 40°, ∠ = C ° 1 55 ;
б) AB = A B1 1, BC = B C1 1, ∠ = B 30°, ∠ = A ° 1 72 , ∠ = C ° 1 78 .
512. Через вершины треугольника проведены прямые, параллельные
противолежащим сторонам. Сколько треугольников, равных данному,
при этом образовалось? Докажите их равенство.
513. Угол одного из двух равных треугольников равен сумме двух
углов другого треугольника. Докажите, что данные треугольники прямоугольные.
514. В треугольниках ABC и MNK AB = MN, ∠ = A M∠ , ∠ ≠ B N∠ .
Может ли треугольник ABC быть равным треугольнику с вершинами M, N, K?
515. Треугольник пересекается четырьмя параллельными прямыми.
Докажите, что по крайней мере одна из них не проходит через вершину
треугольника.
516. Стороны треугольника лежат на прямых, углы между которыми
равны 20°, 30° и 50°. Найдите углы треугольника.
517. Могут ли биссектрисы двух углов треугольника быть взаимно перпендикулярными? Ответ обоснуйте.
518. Докажите, что две высоты треугольника не могут точкой пересечения делиться пополам.
519. Докажите равенство равнобедренных треугольников по боковой
стороне и углу при основании.
520. Треугольники ABC, BCD и DCE равносторонние. Докажите:
а) параллельность прямых AE и BD;
б) равенство треугольников ABD и EDB;
в) равенство треугольников ABE и EDA.
Найдите углы треугольника ABE.

🎥 Видео

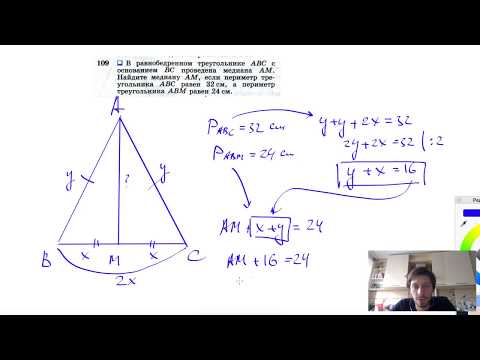
№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать

№542. В подобных треугольниках ABC и KMN стороны АВ и КМ, ВС и MN являются сходственнымиСкачать

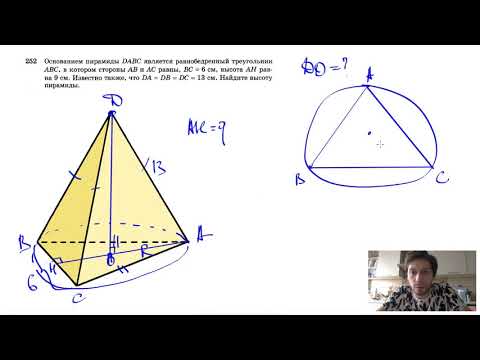
№252. Основанием пирамиды DABC является равнобедренный треугольник ABC, в котором АВ = АС, ВС=6 смСкачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

№566. Равнобедренный треугольник, боковая сторона которого равна m, а угол при основании равен φСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

№158. Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой сторонеСкачать

Равнобедренный треугольник. Практическая часть. 7 класс.Скачать

Свойства равнобедренного треугольника. 7 класс.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

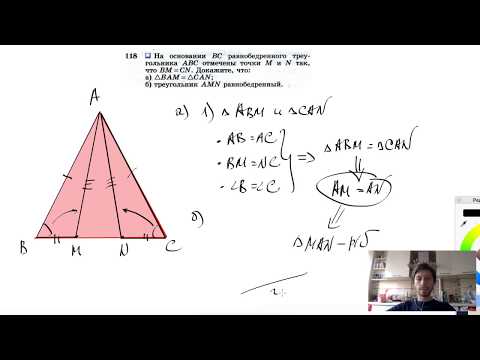
№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать

Решение задач ( Равнобедренный треугольник) 7 классСкачать

№235. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD. Найдите углыСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Жестокая задача о равнобедренных треугольникахСкачать

№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать