Треугольник и точка acmp (5 видео) | Курс школьной геометрии

Точка внутри треугольника

Координаты треугольника

Координаты точки

Вы ввели следующие координаты многоугольника

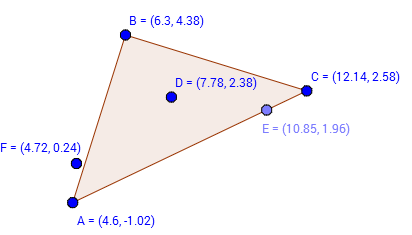
Определение, принадлежит ли произвольная точка какому либо треугольнику (находится ли она внутри треугольника, на самом деле очень важная задача. Для нас она важна в контексте разбиения многоугольника на треугольники. Решение этой промежуточной задачи, позволит нам определять координаты центра тяжести многоугольника.

Итак, существует достаточно много вариантов определения принадлежности точки треугольнику. Могу порекомендовать ссылку. Написано достаточно подробно и рассмотрены практически все варианты.

Мы в своей реализации будем придерживаться следующего алгоритма

Пусть у нас есть треугольник

Высчитаем значение трех нижеуказанных выражений

где x0,y0 — координаты произвольной точки

Если все три значения одинакового знака, то точка внутри треугольника,

если значение равно нулю, значит точка лежит на стороне треугольника

В ином случае (если значения различные по знаку) , точка вне треугольника.

Теперь проверим наше предположение

Точка лежит внутри треугольника так как результат трех вычислений одинаков по знаку ( все они отрицательные)

В этом случае точка F лежит вне треугольника, так как знаки результирующих вычислений различны.

Хотелось бы заметить, что в случае точки Е наш бот, скажет что точка также находится внутри треугольника, хотя и находится на стороне треугольника( или как вариант в одной из вершин) . Это как уже было сказано связано с использованием этого бота, для расчета центра тяжести многоугольников.

Видео:Алгоритмы. Попадание точки в треугольникСкачать

Некоторые задачи вычислительной геометрии

Задача №195. Симметрия

Многие из вас, вероятно, знакомы с понятием симметрии относительно прямой. Пусть на плоскости расположена прямая L и точка A. Точка B называется симметричной точке A относительно прямой L, если отрезок АВ перпендикулярен прямой L и делится пополам точкой пересечения с ней. В частности, если точка А лежит на прямой L, то точка B совпадает с точкой А.

Задана прямая L, параллельная одной из осей координат, и точка А. Найдите точку В, симметричную А относительно L.

Входные данные

Первая строка входного файла INPUT.TXT содержит 4 числа: x1, y1, x2, y2 – координаты двух различных точек, через которые проходит прямая L. Вторая строка входного файла содержит 2 числа xA и yA – координаты точки А. Все числа во входном файле целые и не превосходят 108 по модулю.

Выходные данные

В выходной файл OUTPUT.TXT выведите числа xB и yB – координаты точки B.

№	INPUT.TXT	OUTPUT.TXT
1	0 0 0 1 10 10	-10 10
2	0 0 1 0 10 10	10 -10

Решение

freopen(«input.txt», «r», stdin);

freopen(«output.txt», «w», stdout);

int x1, y1, x2, y2, xa, ya;

int x = xa, y = ya;

Задача №196. Выпуклая оболочка

(Время: 1 сек. Память: 16 Мб)

Рассмотрим бесконечный лист клетчатой бумаги. Закрасим некоторое множество клеток в черный цвет. Теперь мы хотим закрасить минимальное количество клеток, так, чтобы множество черных клеток стало выпуклым.

Напомним, что геометрическая фигура Φ называется выпуклой, если для любых точек A из Φ и В из Φ с вещественными координатами отрезок [AB] принадлежит Φ.

Входные данные

В первой строке входного файла INPUT.TXT содержатся два числа N и M (1 ≤ N, M ≤ 100) — размеры куска бумаги, куда попали все черные клетки. В каждой из следующих N строк содержится М символов «*» или «.». Символ «*» обозначает черную клетку, а «.» белую.

Выходные данные

В выходной файл OUTPUT.TXT выведите выпуклое множество, содержащее минимальное количество дополнительно покрашенных черных клеток, в ровно N строках по M символов «*» или «.» в каждой.

Примеры

№	INPUT.TXT	OUTPUT.TXT
1	2 4 ... .*.	.. ..
2	4 3 .. .. .. ..	.. .. .. ..

Решение

int max_x = -1, max_y = -1, min_x = 101, min_y = 101;

if (i max_x) max_x = i;

if (j max_y) max_y = j;

float alpha = M_PI/n;

float r = a/(2*sin(alpha));

Входные данные

Входной файл INPUT.TXT состоит из двух строк. На каждой строке записана информация об одной окружности – координаты ее центра x и y (целые числа, по модулю не превосходящие 5000) и радиус (целое число 1 ≤ r ≤ 1000).

Выходные данные

В выходной файл OUTPUT.TXT выведите «YES», если окружности пересекаются, и «NO» в противном случае.

Примеры

№	INPUT.TXT	OUTPUT.TXT
1	0 0 2 0 3 2	YES
2	1 1 1 4 4 1	NO

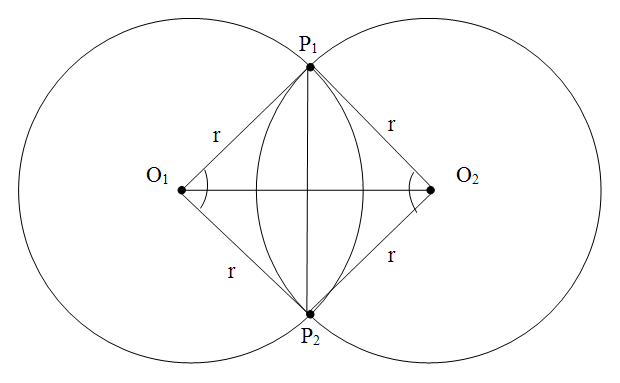
Решение

cin >> x >> y >> r >> x1 >> y1 >> r1;

cout = abs(r-r1)) ?»YES» : «NO»);

Задача №200. Фонарики (acmp.ru)

«Одна голова хорошо, а две лучше. Одна лампочка хорошо, а две лучше!» — подумал Миша, и решил собрать фонарик с двумя лампочками. Теперь он хочет узнать, насколько фонарик с двумя лампочками лучше, чем фонарик с одной. Для этого Миша посветил фонариком на стену, и каждая из лампочек осветила на ней круг.

Эффективность фонарика Миша хочет оценить через площадь освещенной части стены. Миша догадался измерить координаты центров освещенных кругов и их радиусы (которые оказались одинаковыми). Причем, площадь, освещаемая фонариком с одной лампочкой известна, т.к. описана в документации, прилагаемой к фонарику. Но что делать дальше он не знает. Напишите программу, которая поможет Мише.

Входные данные

В первых двух строчках содержатся координаты (x₁,y₁) и (x₂,y₂) — центры кругов от лампочек собранного Мишей фонарика. В третьей строке задан радиус r описанных выше кругов, а четвертая строка содержит площадь освещения s фонариком из одной лампочки. Все числа целые и удовлетворяют следующим ограничениям: 1 ≤ x₁,y₁,x₂,y₂,r ≤ 100, 1 ≤ s ≤ 10 5 . Так же заметим, что площади, освещаемые разными фонариками, отличаются друг от друга более чем на 10 -3 .

Выходные данные

Выведите «YES», если Мишин фонарик лучше старого (т.е. освещает большую площадь) и «NO» в противном случае.

Примеры

№	Ввод	Вывод
1	1 2 3 4 2 22	YES
2	1 1 100100 1 7	NO

Решение

Очевидно, окружности в задаче могут не пересекаться, совпадать, либо пересекаться. Первые два случая тривиальны. Остановимся на последнем. Радиусы пересекающихся окружностей образуют ромб (см. рис.)

Рис. 34. Иллюстрация к задаче «Фонарики» (acmp.ru)

Очевидно, общая площадь q покрытия двух кругов равна сумме их площадей минус площадь криволинейной фигуры, построенной на дугах P₁P₂ обеих окружностей. Обозначим площадь этой фигуры w. Величина w равна удвоенной площади сектора каждого из кругов и её можно найти по формуле из школьного курса геометрии:

Где α – величина угла P₁O₁P₂ (или P₁O₂P₂ , что то же самое) в радианах.

using namespace std;

double x1, y1, x2, y2, r, s, l, alpha, p, q, w;

cin >> x1 >> y1 >> x2 >> y2 >> r >> s;

l = sqrt((x1 — x2) * (x1 — x2) + (y1 — y2) * (y1 — y2));

alpha = 2 * acos(l / 2 / r);

w = (alpha — sin(alpha)) * r * r;

q = l s ? «YES» : «NO»);

Задача №201. Клад (acmp.ru)

(Время: 2 сек. Память: 32 Мб)

Источник задачи: Московская олимпиада по информатике 2002/2003 г.

Найти закопанный пиратами клад просто: всё, что для этого нужно – это карта. Как известно, пираты обычно рисуют карты от руки и описывают алгоритм действий. Большая часть таких действий просто сводится к прохождению какого-то количества шагов в одном из восьми направлений (1 – север, 2 – северо-восток, 3 – восток, 4 – юго-восток, 5 – юг, 6 – юго-запад, 7 – запад, 8 – северо-запад) (см. рис). Длина шага в любом направлении равна 1.

Путешествие по такому пути обычно является прекрасным способом посмотреть окрестности, однако в наше время постоянной спешки ни у кого нет времени на это. Поэтому кладоискатели хотят идти напрямую в точку, где зарыт клад. Например, вместо того, чтобы проходить три шага на север, один шаг на восток, один шаг на север, три шага на восток, два шага на юг и один шаг на запад, можно пройти напрямую, использовав около 3.6 шага (см. рисунок).

Вам необходимо узнать точку, в которой находится клад согласно указаниям пиратов.

Видео:Задача 971. Треугольник - 4. acmp.ru C++Скачать

Треугольник и точка acmp

Задача. Даны координаты трех точек (A),(B),(C). Точки расположены так, что образуют треугольник. Дана еще одна точка (D). Необходимо проверить лежит ли эта точка внутри треугольника (triangle ABC). Написать код программы на #С++.

Решение. Сразу заметим, что здесь будет предложено решение, которое нельзя назвать наилучшим. Это — быстрое решение, но имеет целый ряд недостатков. Классическая идея для решения состоит в том, что если точка (D) лежит внутри треугольника (triangle ABC), то получаются три треугольника, содержащихся внутри данного и сумма их площадей должна равняться площади данного треугольника. Т.е. должно выполняться равенство: [S_=S_+S_+S_] А теперь поясним проблему. Вам придется сравнивать значения двух действительных чисел — площадь данного треугольника и сумму площадей трех внутренних треугольников. А, как известно, это можно сделать только с определенной точностью. На практике рассматривают разность этих площадей по модулю и сравнивают с маленьким числом, задающим точность сравнения. А это плохо.

Для решения задачи воспользуемся другой идеей:

Все точки треугольника (и любого выпуклого многоугольника) должны лежать по одну сторону от прямой, проходящей через каждую его сторону.

Запишем уравнение прямой, проходящей, например, через точки A и B. Получим: [left( x — x_A right) left( y_B — y_A right) — left( y — y_A right) left( x_B — x_A right) = 0]. Уравнение записано в такой форме, чтобы не приходилось выполнять деление и переживать о нуле в знаменателе.

Теперь для любой точки (left( x;y right)) мы можем вычислить левую часть приведенного равенства. Для точек, лежащих на прямой мы должны получать ноль. В тоже время прямая разобьёт плоскость на две полуплоскости. Точки лежащие в одной полуплоскости будут давать положительные значения. А точки из другой полуплоскости — отрицательные.

Мы готовы проверить первое условие — принадлежит ли точка D (left( x_d,y_d right)) той же полуплоскости, что и точка C (left( x_c,y_c right)) относительно прямой (left( AB right)) ? Для этого подставим обе точки в левую часть приведенного выше уравнения прямой и убедимся, что получены значения одного и того же знака. А если одна из точек даст точно ноль? Это означает, что точка лежит на прямой. По условию задачи это может быть только точка D. Тогда она принадлежит треугольнику независимо от знака выражения, вычисленного для точки C.

Приведем код простенькой программы на С++. Вам надо ввести координаты трех вершин треугольника на плоскости, а затем координат точки, принадлежность которой треугольнику проверяется. Вот код программы. Проверить работу программы онлайн можно на нашем компиляторе здесь. Скопируйте код программы (ctrl+c) и вставьте (ctrl+v) в компилятор вместо программы по умолчанию.