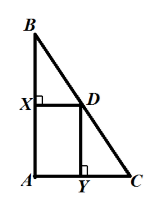Треугольник через 4 точки

Математика | 5 — 9 классы

Через четыре точки проведите три отрезка так, чтобы образовался треугольник.

Нарисуй 4 точки и рисуу трегольник.

Точки необязатльно должны быть вершинами.

На одной из сторон будет две точки ВСЁ.

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Проведи в квадрате два отрезка так, чтобы получилось четыре треугольника и четырехугольник?

Проведи в квадрате два отрезка так, чтобы получилось четыре треугольника и четырехугольник.

Видео:четыре замечательные точки треугольника 8 КЛАСС АтанасянСкачать

Из точки, не лежащей на прямой, проведено к этой прямой 7 отрезков?

Из точки, не лежащей на прямой, проведено к этой прямой 7 отрезков.

Сколько треугольников на полученном рисунке?

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Проведи в квадрате два отрезка так, чтобы получилось четыре треугольника и четырёхугольник?

Проведи в квадрате два отрезка так, чтобы получилось четыре треугольника и четырёхугольник.

Видео:Треугольник - 3 точки?Скачать

На прямой отметили четыре точки?

На прямой отметили четыре точки.

Образовалось 6 отрезков с концами в этих точках.

Видео:№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать

Номер 359 на прямой отметили четыре точки?

Номер 359 на прямой отметили четыре точки.

Образовалось 6 отрезков с концами в этих точках.

Видео:Как 4 линиями соединить 9 точек?Скачать

Через четыре точки , расположенные по углам прямоугольника провести три отрезка, чтобы получился треугольник?

Через четыре точки , расположенные по углам прямоугольника провести три отрезка, чтобы получился треугольник.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Через четыре точки , расположенные по углам прямоугольника провести три отрезка, чтобы получился треугольник?

Через четыре точки , расположенные по углам прямоугольника провести три отрезка, чтобы получился треугольник.

Видео:Геометрия 8 класс. Четыре замечательные точки треугольникаСкачать

Начертите четырёхугольник ABCD : отметь точку M — середину отрезка CD?

Начертите четырёхугольник ABCD : отметь точку M — середину отрезка CD.

Проведите отрезки AC и AM.

Назовите все образовавшиеся многоугольники.

Видео:Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

Через точку О проведите четыре различных прямых?

Через точку О проведите четыре различных прямых.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Начертите четырёхугольник АБСД отметьте точку Е — середину отрезка АД проведите отрезки АС и СЕ назовите все образовавшиеся многоугольники?

Начертите четырёхугольник АБСД отметьте точку Е — середину отрезка АД проведите отрезки АС и СЕ назовите все образовавшиеся многоугольники.

На странице вопроса Через четыре точки проведите три отрезка так, чтобы образовался треугольник? из категории Математика вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

1)5 + 4 = 9(кг) — всего купила 2)1890 : 9 = 210(тг) — за 1 кг 3)210 * 4 = 840(тг) — за 4 кг 4)210 * 5 = 1050(тг) — за 5 кг.

Х будет рано 8, 1. Простое же уравнение.

А + b = 7620, a — b = 5028 ; a = 4295, a — b = 4295 ; b = 52100, a + b = 104248 ; a = 8500, a — b = 7500. Удачи)).

1 k = 9140 2 c = 3375 это легко.

Всего в магазин привезли 63 кг конфет. За день пришло 3 покупателя. Каждый покупатель купил по 9 кг конфет. Вопрос : Сколько осталось конфет в магазине? Пойдёт.

У Жени было 63 рубля , он купил 9 тетрадей по 3 р. Сколько осталось денег у Жени.

S = x * (1 + %) ^ n S = 150000(1 + 0. 14) ^ 3 = 150000 * 1. 14 ^ 3 = 222231. 6 Ответ : 222231. 6.

9) 10) Человек, стоящий на пляже, видит горизонт на 5, 6 км. Значит, Человек на пляже возвышается над горизонтом на 2, 45 м. Или он такого роста (что вряд ли), или он стоит на кучке песка. Если он хочет видеть горизонт на 7, 2 км, то должен под..

1)178 а остаток1, 178 умножаем на 2 = 356 + 1 = 3572)184 а остаток 2, 184умножаем на 3 = 552 + 2 = 5543)161 а остаток 3, 161 умножаем на 4 = 644 + 3 = 6474)122 а остаток 2, 122 умножаем на 6 = 732 + 2 = 735.

Один человек, так как для всего нетрудно много дел.

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Вопрос, на который я не ответил. И почему.

Я был на встрече. Общались с коллегами по одному из проектов. Неожиданно разговор затронул, как оказалось по итогам, интересную тему.

Задача:

Объединить все четыре точки тремя линиями. При том, что ни одна из трех линий не должна проходить через центр.

Тридцать секунд раз размышление – время пошло. Думаем.

Четыре стороны. Четыре стороны – это четыре линии. Казалось бы, глупо пытаться прокладывать линии от точки к точке, ведь линии всего три. И, тем не менее, ты упорно начинаешь это делать. И так и сяк – никак. Перебрал все точки, все стороны – никак. Наклонил голову – нет. Вот уже и пять секунд, и десять – снова нет. Что делать? Ты же умный парень, подумай — где-то подвох! Точно. В чем-то фокус. Меня обманули! Да, нет, не могли.

ОК, пауза. Собрались.

Еще раз к задаче. Точки четыре, линии три. И в центр нельзя. Может линии не прямые?! — кидаешь ты себе, уже даже смятении. Но нет – это же линии. Давай еще раз переберем все точки по одной. Направо, налево. Пять секунд, четыре, две. Время закончилось. Не знаю.

— Ребят, я не знаю! Ответ скажете?!

— Конечно, скажем, братан. Лови.

Как показали ответ, ты думаешь – «Бог, мой! Что за идиот я! Все же так казалось бы просто!».

А теперь в чем суть.

Я долго думал над этим. Смысл в том, что решение задачи показывает не то, насколько ты глуп или умный. Решение показывает то, как ты мыслишь. Насколько развит твой мозг не с точки зрения книг или навыков, а с точки зрения физиологии восприятия. Решение показывает, готов ли ты выйти за рамки. Перешагнуть за горизонт. Насколько ты за шорен и способен ли мыслить глобально. Ведь, никто не говорил, что нельзя выходить за рамки квадрата. Квадрата, Карл! Ты сам представил себе этот квадрат! В задаче сказано объединить четыре точки тремя линиями не проходя через центр. А ты представил квадрат и все тридцать секунд не знал, куда себя деть из его узких рамок. Тебе не сказали, что это квадрат! Ты сам себе его выдумал! Сам себя ограничил! Сам!

Сделай выводы — мысли шире. Проблема не может быть решена на том уровне, на котором она поставлена. Предела нет. Нет рамок. Нет горизонта. Лишь те, что себе поставил ты сам.

Как этому научится? Пока не знаю. Это же физиология. Наверное, тот самый IQ. И парень я, вроде, не глупый. Я же отнесся серьезно. Я же искал ходы. Искал варианты. 30 секунд. Я хотел найти ответ — не получилось.

Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

Четыре замечательные точки треугольника

Вы будете перенаправлены на Автор24

В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.

Видео:Уравнения стороны треугольника и медианыСкачать

Точка пересечения медиан треугольника

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

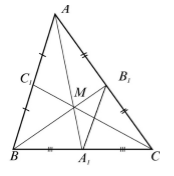
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Видео:№4. Точки А, В, С и D не лежат в одной плоскости, а) Могут ли какие-то три изСкачать

Точка пересечения биссектрис треугольника

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

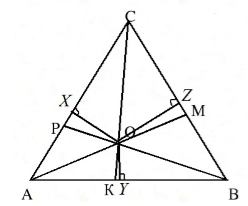
Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Готовые работы на аналогичную тему

Для доказательства нам потребуется следующая теорема.

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Точка пересечения серединных перпендикуляров треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

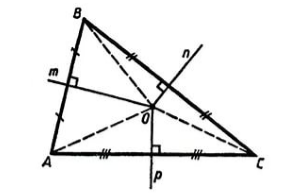
Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Видео:Головоломка Соедини одинаковые цифрыСкачать

Точка пересечения высот треугольника

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

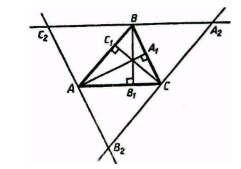
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Пример задачи на использование 4 замечательных точек треугольника

Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что

а) точка $D$ — середина стороны $BC$.

б) $angle A=angle B+angle C$

Решение.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.

б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2021

📹 Видео

Окружность вписанная в треугольник и описанная около треугольника.Скачать

8 класс - Геометрия - Четыре замечательные точки треугольникаСкачать

Геометрия. 8 класс. Четыре замечательные точки треугольника.Скачать