Треугольник abc вписанный в окружность делит ее на три

Вопрос по геометрии:

Треугольник ABC, вписанный в окружность, делит её на три дуги. Вычисли градусную меру третьей дуги и углы треугольника, если известны две другие дуги: ∪AB=80° и ∪BC=170°.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Дуга АС=360°-(80°+170°)=110°
угол А=170:2=86°(половина дуги ВС)
угол В=110:2=55°(половина дуги АС)
угол С= 80:2=40°(половина дуги АВ)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Треугольник ABC, вписанный в окружность, делит её на три дуги?

Геометрия | 5 — 9 классы

Треугольник ABC, вписанный в окружность, делит её на три дуги.

Вычисли градусную меру третьей дуги и углы треугольника, если известны две другие дуги : ∪AB = 80° и ∪BC = 170°.

Дуга АС = 360° — (80° + 170°) = 110°

угол А = 170 : 2 = 86°(половина дуги ВС)

угол В = 110 : 2 = 55°(половина дуги АС)

угол С = 80 : 2 = 40°(половина дуги АВ).

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В треугольнике ABC угол B равен 52 градуссам какая дуга окружности будет иметь градусную меру 104 градусса варианты ответов : 1) дуга BC 2) дуга AC 3) дуга AB 4) и дуга AC и дуга BC 5) и дуга AC и дуг?

В треугольнике ABC угол B равен 52 градуссам какая дуга окружности будет иметь градусную меру 104 градусса варианты ответов : 1) дуга BC 2) дуга AC 3) дуга AB 4) и дуга AC и дуга BC 5) и дуга AC и дуга AB.

Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

В окружность вписан треугольник ABC так, что AB — диаметр окружности?

В окружность вписан треугольник ABC так, что AB — диаметр окружности.

Найти углы треугольника, если дуга AC равна 70 градусам.

Видео:Решение задачи №1 из ЕГЭ математикаСкачать

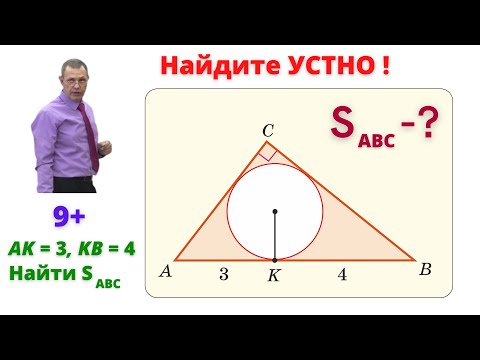
Вершины треугольника АВС, вписанного в окружность, делят его на дуги, длины которых относятся как 2 : 3 : 4, найдите градусную меру наименьшего угла треугольника АВС?

Вершины треугольника АВС, вписанного в окружность, делят его на дуги, длины которых относятся как 2 : 3 : 4, найдите градусную меру наименьшего угла треугольника АВС.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

А)две точки делят окружность на дуги, градусные меры которых пропорциональны числам 2 и 7?

А)две точки делят окружность на дуги, градусные меры которых пропорциональны числам 2 и 7.

Какова градусная мера каждой из этих дуг?

Б)точки К и М делят окружность на две дуги, градусная мера одной из них в 5 раз больше другой.

Чему равна градусная мера каждой из этих дуг?

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

В окружность вписан треугольник ABC так, что АВ — диаметр окружности?

В окружность вписан треугольник ABC так, что АВ — диаметр окружности.

Найдите углы треугольника, если : дуга ВС = 134° ;

Видео:Геометрия К окружности, вписанной в треугольник ABC, проведены три касательные (см. рис.)Скачать

Треугольник ABC вписан в окружность?

Треугольник ABC вписан в окружность.

Известны два его угла ∠A = 80 ∘, ∠B = 55 ∘.

Найдите градусную меру меньшей дуги.

Видео:Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

Треугольник ABC вписан в окружность?

Треугольник ABC вписан в окружность.

Известны два его угла

Найдите градусную меру меньшей дуги AB.

Видео:Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскостиСкачать

Найдите углы треугольника ABC, вписанного в окружность, если m ( дуги AB) = 50, m( дуги AC) = 80?

Найдите углы треугольника ABC, вписанного в окружность, если m ( дуги AB) = 50, m( дуги AC) = 80.

Видео:№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать

Найти углы равнобедренного треугольника вписанного в окружность основаник которого стягивает дугу градусная мера которой 49°?

Найти углы равнобедренного треугольника вписанного в окружность основаник которого стягивает дугу градусная мера которой 49°.

Видео:ЕГЭ Математика Задание 6#27935Скачать

Хорда делит окружность на две дуги, градусные меры которых относятся как 1 : 5?

Хорда делит окружность на две дуги, градусные меры которых относятся как 1 : 5.

Найдите вписанный угол, опирающийся на меньшую из этих дуг.

На странице вопроса Треугольник ABC, вписанный в окружность, делит её на три дуги? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Видео:Геометрия Вершины равнобедренного треугольника ABC (AB = BC) делят описанную около него окружностьСкачать

Треугольник вписанный в окружность

Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Вписанная окружность. ЗАДАЧА ИЗ ГОНКОНГА!Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Вписанная окружность делит чевиану пополам. ЗАДАЧА - БЛЕСК!Скачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

📹 Видео

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Углы, вписанные в окружность. 9 класс.Скачать

Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть I)Скачать

Волшебная формула для вписанной окружностиСкачать