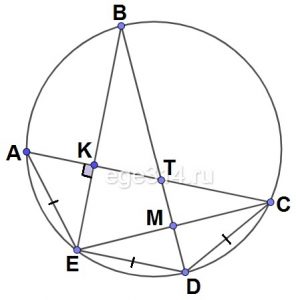
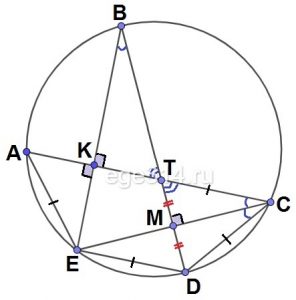
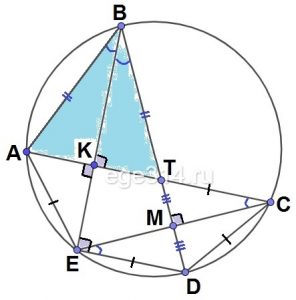
Задание 16. Точки А, В, С, D и Е лежат на окружности в указанном порядке, причём АЕ = ED = CD, а прямые АС и BE перпендикулярны. Отрезки АС и BD пересекаются в точке Т.
а) Докажите, что прямая ЕС пересекает отрезок TD в его середине.
б) Найдите площадь треугольника АВТ, если BD = 6, АЕ = √6.
а) Обозначим точку пересечения прямой ЕС и отрезка TD через М, а точку пересечения отрезков АС и BE через Н. Угол ВМС равен полусумме дуг ВС и DE, а угол ВНС равен полусумме дуг ВС и АЕ. Дуги АЕ, ED и CD меньше 180° и стягиваются равными хордами. Следовательно, эти дуги равны. Значит,
В треугольнике TCD отрезок СМ является биссектрисой и высотой, поэтому этот, треугольник равнобедренный, ТС = CD, а точка М — середина отрезка TD.
б) Дуги АЕ и CD равны, значит, 
Обозначим угол DBE через α. Тогда:


В треугольнике АВТ отрезок ВН является биссектрисой и высотой, поэтому этот треугольник равнобедренный, АВ = ВТ, а точка Н — середина отрезка AT. Получаем:
Значит, площадь треугольника ABT, равна:
Ответ:
Видео:Геометрия Вершины квадрата ABCD лежат на окружности. На дуге AB отмечена произвольная точка MСкачать

Точки A, B, C, и D лежат на одной окружности так, что хорды
Точки A, B, C, и D лежат на одной окружности так, что хорды AB и CD взаимно перпендикулярны, а угол BDC = 25°. Найдите величину угла ACD.
Решение:
Рассмотрим треугольник ∆BDO он прямоугольный.
Так как по условию хорды AB и CD перпендикулярны. Найдем угол OBD из ∆BDO:
180°-90°-25°=65° угол OBD
Углы OBD=ACD так как опираются на одну дугу AD
Угол ACD=65°
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами..
Видео:№665. Вершины треугольника ABC лежат на окружности. Докажите, что если АВ — диаметр окружностиСкачать
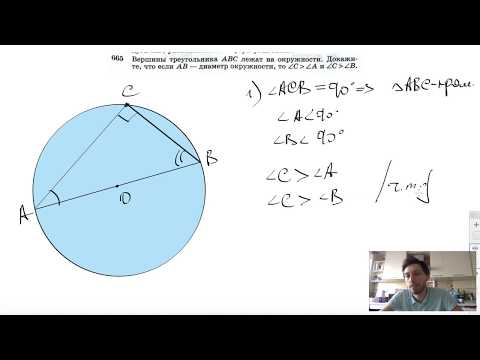
Решение №2311 Точки A, B, C, D и E лежат на окружности в указанном порядке, причем AE = ED = CD, а прямые AC и BE перпендикулярны.
Точки A, B, C, D и E лежат на окружности в указанном порядке, причем AE = ED = CD, а прямые AC и BE перпендикулярны. Отрезки AC и BD пересекаются в точке T.
а) Докажите, что прямая EC пересекает отрезок TD в его середине.
б) Найдите площадь треугольника ABT, если BD = 6, АЕ = sqrt .
Источник: Ященко ЕГЭ 2022 (36 вар)
AE = ED = CD, AC⊥BE, Т – точка пересечения АС и ВD.
Обозначим: К – точка пересечения АС и ВЕ, М – точка пересечения СЕ и DT.
а) Доказать: DM = МТ .
∠ЕВК = ∠АСЕ = ∠ECD = ∠CED = ∠α – как вписанные углы окружности опирающиеся на равные дуги ‿ED = ‿AE = ‿CD (равны хорды стягивающие дуги).
Т.к. AC⊥BE, то ∠ВКТ = 90°.
Рассмотрим ΔКВТ и ΔТСМ, в них ∠КТВ = ∠СТМ – вертикальные, ∠КВТ = TCM – совпадающие с вписанными углами. Сумма углов в треугольнике равна 180°, значит и третьи углы равны ∠ВКТ = ∠ТМС = 90°.
В ΔТСD МС является медианой и высотой, значит треугольник равнобедренный, МС медиана, тогда DM = МТ.
Что и требовалось доказать.
б) ВD = 6, АЕ = sqrt . Найти: SΔАВТ .
В ΔАВТ ВК биссектриса (∠АВЕ = ∠КВТ, как совпадающие с вписанными опирающимися на равные дуги) и высота (∠ВКТ = 90°), значит и медиана, треугольник равнобедренный, боковые стороны равны АВ = ВТ.
Площадь ΔАВТ будем искать как половину произведения его сторон на синус угла между ними:
Прямая ЕС пересекает прямые АС и ЕD, образованные накрест лежащие углы равны ∠АСЕ = ∠СЕD (как вписанные опирающиеся на равные дуги), значит АС||ED. КЕ секущая к этим же прямым, накрест лежащие углы равны ∠АКЕ = ∠КЕD = 90°.
Треугольник ВЕD – прямоугольный (∠КЕD = 90°) вписан в окружность, значит его гипотенуза является диаметром окружности D = 2R = BD = 6.
По теореме синусов найдём sin α :
Найдём cos α :
cos 2 α + sin 2 α = 1
Найдём sin∠AВТ = sin 2α (∠AВТ = ∠АВК + ∠КВТ = α + α = 2α):
ТС = DC = AE = sqrt . Из прямоугольного ΔМТС найдём МТ:
6·MT = sqrt · sqrt
6·MT = 6
MT = 1
Найдём DT:
DT = 2·МТ = 2·1 = 2
Найдём ВТ = ВА:
ВТ = ВА = BD – DT = 6 – 2 = 4
Найдём площадь треугольника АВТ:
S_=fraccdot ABcdot BTcdot sin angle ABT=fraccdot 4cdot 4cdot frac<sqrt>=frac<8sqrt>
📸 Видео
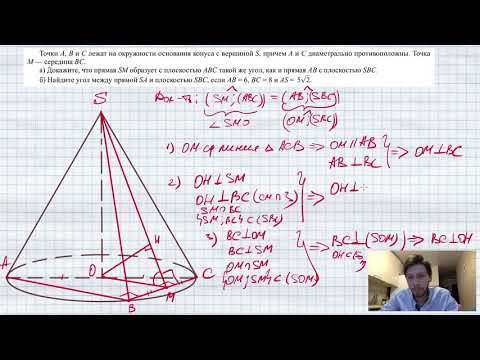
Точки A, B и C лежат на окружности основания конуса с вершиной S, причем A и C диаметрально противопСкачать
2020 точка О центр окружности на которой лежат точки A B и C известно что Угол ABC равен 62 градусаСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Задача 6 №27873 ЕГЭ по математике. Урок 114Скачать

№960. Какие из точек А (3; -4), В(1; 0), С(0; 5),Скачать

2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

2034 треугольник ABC вписан в окружность с центром в точке O точки O и C лежат в одной полуплоскостиСкачать

2017 на окружности по разные стороны от диаметра AB взяты Точки M и NСкачать

Доказать, что точки лежат на одной окружностиСкачать

ОГЭ 2020 задание 16Скачать
ОГЭ Задание 25 Условие принадлежности четырёх точек одной окружностиСкачать

На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

№118. Точки А, М и О лежат на прямой, перпендикулярной к плоскости α, а точки О, В, С и D лежатСкачать