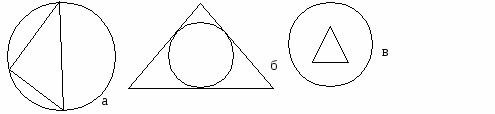тест по геометрии (8 класс)
Тест по геометрии по теме: «Вписанные и описанные окружности»
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Тест по теме «Вписанные и описанные окружности» (8 класс)
- Тест вписанная окружность 8 класс с ответами
- Тест по геометрии по теме: «Вписанные и описанные окружности» тест по геометрии (8 класс)
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- тест по математике 8 класс
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Тест по теме » Вписанная и описанная окружности» по геометрии 8 класс
- Просмотр содержимого документа «Тест по теме » Вписанная и описанная окружности» по геометрии 8 класс»
- 💡 Видео
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Скачать:
| Вложение | Размер |
|---|---|
| test.docx | 14.44 КБ |
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Предварительный просмотр:
Тест по геометрии по теме: «Вписанные и описанные окружности»
Центр вписанной в треугольник окружности является точкой пересечения .
- медиан
- биссектрис
- высот
- серединных перпендикуляров
- мне стыдно, но я не знаю ответ на этот элементарный вопрос
Четырёхугольник ABCD вписан в окружность. Угол BAD равен 50 0 , а угол АВС равен 95 0 . Найдите разность между углами BCD и ADC.
В параллелограмм с периметром 40√2 и углом 45 0 вписана окружность. Найдите её радиус.
Найдите площадь прямоугольного треугольника, если радиус вписанной в него окружности равен 5 см, а гипотенуза 23 см.
- 140
- 120
- 90
- 45
- Ничего не хочу знать про прямоугольные треугольники. Мне и без них хорошо.
Найдите площадь прямоугольной трапеции, если её меньшее основание равно 6 см, а радиус вписанной в неё окружности 4 см.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

По теме: методические разработки, презентации и конспекты
Урок геометрии в 8 классе по теме «Вписанная и описанная окружность»
Презентация к уроку включает определения основных понятий, создание проблемной ситуации, а также развитие творческих способностей учащихся.
Диктант по геометрии в 8 классе. Тема » Вписанные и описанные окружности»
Диктант можно использовать на уроке систематизации знаний перед контрольной работой. Вопросы диктанта появляются по щелчку левой мыши.
Презентация к уроку геометрии 8 класса по теме » Описанная окружность»
Презентация к уроку.
Презентация «Урок геометрии по теме: «Вписанные углы»
Презентация. На уроке дается определение вписанного угла, теорема о вписанном угле и следствия из него.
Конспект урока геометрии 8 класс по теме: «Вписанная и описанная окружность» Атанасян.
Конспект урока геометрии 8 класса по теме: «Вписанная и описанная окружность» автор учебника Атанасян.
Тест по теме «Правильный многоугольник. Вписанная и описанная окружности. Формулы площади правильного многоугольника , стороны правильного многоугольника и радиуса вписанной окружности в правильный многоугольник»
Тест по теме «Правильный многоугольник. Вписанная и описанная окружности. Формулы площади правильного многоугольника , стороны правильного многоугольника и радиуса вписанной окр.
Технологическая карта урока геометрии на тему: «Вписанный угол»
Урок «открытия» нового знания. Первый урок по теме. Определение темы занятия в сотрудничестве с обучающимися. Направить обучающихся на самостоятельное определение целей и задач занятия, те.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Тест по теме «Вписанные и описанные окружности» (8 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.

- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.

- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
- Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
- Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
- Около любого треугольника можно ___________________________.
- Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
- Центром вписанной в треугольник окружности является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника.
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
- Описанная около треугольника
окружность изображена на рисунке:
- Вписанная в четырехугольник окружность изображена на рисунке:
- В треугольник можно вписать только _________________________.


- Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
- Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
- В четырехугольник можно вписать окружность, если __________________________________________________________.
- В любой треугольник можно ___________________________.
- Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
- Центром описанного около окружности треугольника является точка пересечения:
— Серединных перпендикуляров к сторонам треугольника
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
— 
— 
- Вписанная в треугольник
окружность изображена на рисунке:
- Описанная около четырехугольника окружность изображена на рисунке:
- Около треугольника можно описать только ____________________.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Тест вписанная окружность 8 класс с ответами
Видео:Геометрия 9 класс. Вписанные и описанные окружности. Ключевая задача № 4.Скачать

Тест по геометрии по теме: «Вписанные и описанные окружности»
тест по геометрии (8 класс)
Тест по геометрии по теме: «Вписанные и описанные окружности»
Видео:Тема 7. Вписанные и описанные окружности треугольникаСкачать

Скачать:
| Вложение | Размер |
|---|---|
| test.docx | 14.44 КБ |
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Предварительный просмотр:
Тест по геометрии по теме: «Вписанные и описанные окружности»
Центр вписанной в треугольник окружности является точкой пересечения .
- медиан
- биссектрис
- высот
- серединных перпендикуляров
- мне стыдно, но я не знаю ответ на этот элементарный вопрос
Четырёхугольник ABCD вписан в окружность. Угол BAD равен 50 0 , а угол АВС равен 95 0 . Найдите разность между углами BCD и ADC.
В параллелограмм с периметром 40√2 и углом 45 0 вписана окружность. Найдите её радиус.
Найдите площадь прямоугольного треугольника, если радиус вписанной в него окружности равен 5 см, а гипотенуза 23 см.
- 140
- 120
- 90
- 45
- Ничего не хочу знать про прямоугольные треугольники. Мне и без них хорошо.
Найдите площадь прямоугольной трапеции, если её меньшее основание равно 6 см, а радиус вписанной в неё окружности 4 см.
Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

По теме: методические разработки, презентации и конспекты
Урок геометрии в 8 классе по теме «Вписанная и описанная окружность»
Презентация к уроку включает определения основных понятий, создание проблемной ситуации, а также развитие творческих способностей учащихся.
Диктант по геометрии в 8 классе. Тема » Вписанные и описанные окружности»
Диктант можно использовать на уроке систематизации знаний перед контрольной работой. Вопросы диктанта появляются по щелчку левой мыши.
Презентация к уроку геометрии 8 класса по теме » Описанная окружность»
Презентация к уроку.
Презентация «Урок геометрии по теме: «Вписанные углы»
Презентация. На уроке дается определение вписанного угла, теорема о вписанном угле и следствия из него.
Конспект урока геометрии 8 класс по теме: «Вписанная и описанная окружность» Атанасян.
Конспект урока геометрии 8 класса по теме: «Вписанная и описанная окружность» автор учебника Атанасян.
Тест по теме «Правильный многоугольник. Вписанная и описанная окружности. Формулы площади правильного многоугольника , стороны правильного многоугольника и радиуса вписанной окружности в правильный многоугольник»
Тест по теме «Правильный многоугольник. Вписанная и описанная окружности. Формулы площади правильного многоугольника , стороны правильного многоугольника и радиуса вписанной окр.
Технологическая карта урока геометрии на тему: «Вписанный угол»
Урок «открытия» нового знания. Первый урок по теме. Определение темы занятия в сотрудничестве с обучающимися. Направить обучающихся на самостоятельное определение целей и задач занятия, те.
Видео:Урок по теме ВПИСАННАЯ ОКРУЖНОСТЬСкачать

тест по математике 8 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Тест по теме «Вписанная окружность»
8 класс, задания базового уровня, которые должны уметь выполнять все учащиеся
Данный тест состоит из 8 заданий, форма заданий открытая, на каждый вопрос три варианта ответа. Каждое верно выполненное задание оценивается в 1 балл.
Время выполнения теста – 10 минут.
6-7 баллов – оценка «4».
5-6 баллов – оценка «3».
Тест можно использовать в конце изучения темы «Вписанная окружность».
Тест ориентирован на работу с базовым учебником: Л. С. Атанасян, В.Ф. Бутузов и другие. Геометрия: 7-9 класс (М.: Просвещение).
с последующей самопроверкой. Ответы нужно записать на двух листочках, один из которых сдаётся на проверку учителю.
1. Центр вписанной в треугольник окружности совпадает с точкой пересечения его…
в) серединных перпендикуляров.
2.Центр вписанной в треугольник окружности равноудалён от…
3. Центр вписанной в треугольник окружности является точкой пересечения его медиан. Этот треугольник…
4. Окружность называется вписанной в многоугольник, если…
а) все его стороны касаются окружности;
б) все его вершины лежат на окружности;
в) все его стороны имеют общие точки с окружностью.
5. Радиус вписанной в треугольник окружности равен расстоянию от центра окружности до…
а) сторон треугольника;
б) вершин треугольника;
в) углов треугольника.
6. Центр вписанной в равнобедренный треугольник окружности может лежать…
а) на любой из его высот;
б) на любой из его медиан;
в) на любом из его серединных
7. Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Этот треугольник может быть…
б) только равносторонним;
8. Многоугольник называется описанным около окружности, если …
а) окружность имеет общие точки с его
б) окружность проходит через его
в) окружность является касающейся всех
Краткое описание документа:
Тест по теме «Вписанная окружность»
8 класс, задания базового уровня, которые должны уметь выполнять все учащиеся
Данный тест состоит из 8 заданий, форма заданий открытая, на каждый вопрос три варианта ответа. Каждое верно выполненное задание оценивается в 1 балл.
Время выполнения теста – 10 минут.
6-7 баллов – оценка «4».
5-6 баллов – оценка «3».
Тест можно использовать в конце изучения темы «Вписанная окружность».
Тест ориентирован на работу с базовым учебником: Л. С. Атанасян, В.Ф. Бутузов и другие. Геометрия: 7-9 класс (М.: Просвещение).
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 954 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 684 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 309 человек из 67 регионов
Ищем педагогов в команду «Инфоурок»
Видео:КОНТРОЛЬНАЯ РБ 9 класс Вписанные и описанные окружностиСкачать

Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 504 389 материалов в базе
Другие материалы
- 04.12.2014
- 601
- 0
- 04.12.2014
- 576
- 0
- 04.12.2014
- 610
- 0
- 04.12.2014
- 656
- 0
- 04.12.2014
- 1278
- 2
- 04.12.2014
- 560
- 0
- 04.12.2014
- 5156
- 184
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 04.12.2014 4592
- DOCX 29 кбайт
- 19 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Клешня Надежда Аркадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 45604
- Всего материалов: 40
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Вписанные и описанные окружности. Геометрия 9 класс. Ключевая задача № 3.Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Школы Москвы будут самостоятельно принимать решение о длительности карантина
Время чтения: 1 минута
Половина российских родителей не одобряют увлечение их детей просмотром видеоблогов
Время чтения: 2 минуты
В Сыктывкаре школьников переведут на дистанционное обучение
Время чтения: 1 минута
Минпросвещения намерено решить вопрос с третьей сменой в школах в 2023 году
Время чтения: 1 минута
Школы Пскова перевели на дистанционное обучение
Время чтения: 2 минуты
В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

Тест по теме » Вписанная и описанная окружности» по геометрии 8 класс
Цель данного теста – проверить уровень усвоения теоретического материала по данной теме.
Просмотр содержимого документа
«Тест по теме » Вписанная и описанная окружности» по геометрии 8 класс»
Муниципальное бюджетное общеобразовательное учреждение
« Выделянская средняя общеоразовательная школа»
Родионово-Несветайского района Ростовской области
Лященко Людмила Егоровна, учитель математики и биологии
Тест по теме «Вписанная и описанная окружности»
Цель данного теста – проверить уровень усвоения теоретического материала по данной теме.
Тест по теме «Вписанная и описанная окружности».
1. Каждая точка биссектрисы неразвернутого угла равноудалена от его
а) углов; б) сторон; в) вершин.
2. Каждая точка серединного перпендикуляра к отрезку
а) равноудалена от концов этого отрезка;
б) равноудалена от середины этого отрезка;
в) равноудалена от углов.
3. Если все стороны многоугольника касаются окружности, то окружность называется
а) описанной около многоугольника;
б) вписанной в треугольник;
в) вписанной в многоугольник.
4. В любой треугольник можно вписать только
а) две окружности;
б) три окружности
в) одну окружность.
5. В любом вписанном четырехугольнике сумма противолежащих углов равна
а) 360 0 ; б) 180 0 ; в) 90 0 .
6. Центр вписанной окружности лежит в точке пересечения
б) серединных перпендикуляров;
7. Описанная около треугольника окружность изображена на рисунке:
8. Вписанная в четырехугольник окружность изображена на рисунке:
Тест по теме «Вписанная и описанная окружности».
1. Каждая точка, равноудаленная от сторон угла, лежит на его
а) медиане; б) высоте; в) биссектрисе.
2. Серединным перпендикуляром к отрезку называется прямая,
а) проходящая через середину данного отрезка и перпендикулярная к нему;
б) проходящая через середину данного отрезка;
в) перпендикулярная к отрезку.
3. Если все вершины многоугольника лежат на окружности, то окружность называется
а) описанной около многоугольника;
б) описанной около треугольника;
в) вписанной в многоугольник.
4. Около любого треугольника можно описать только
а) две окружности;
б) одну окружность;
в) три окружности.
5. В любом описанном четырехугольнике суммы противолежащих сторон
а) равны; б) равны радиусу; в) равны периметру.
6. Центр описанной окружности лежит в точке пересечения
б) серединных перпендикуляров;
7. Вписанная в треугольник окружность изображена на рисунке:
8. Описанная около четырехугольника окружность изображена на рисунке:
I вариант 1б; 2а; 3в; 4в; 5б; 6в; 7а; 8б.
II вариант 1в; 2а; 3а; 4б; 5а; 6б; 7б; 8в.
Л.С. Атанасян, В.Ф. Бутузов и др. «Геометрия 7-9», учебник для общеобразовательных учреждений, Москва, «Просвещение», 2012 г.
Н.Ф. Гаврилова «Поурочные разработки по геометрии 8 класс», Москва, «ВАКО», 2006 г.
💡 Видео
Вписанная и описанная окружности. ЗадачиСкачать

Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Вписанные и описанные окружности. С. р. 3 в1 9 классСкачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Тема 9. Вписанные и описанные четырехугольникиСкачать







 Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:


 Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

 Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:


 Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

 Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:


 Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

 Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
 Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

 Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
 Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

 Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
 Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

 Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
 Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

 Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
 Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

 Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
 Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

 Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
 Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство: