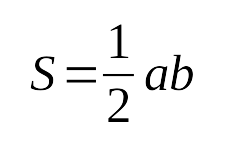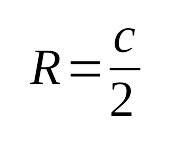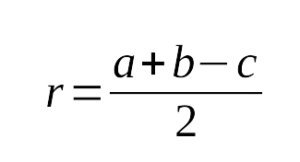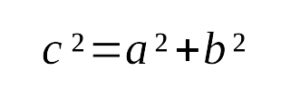- Определение
- Свойства прямоугольного треугольника
- Признаки равенства прямоугольных треугольников
- Признаки прямоугольного треугольника
- Признаки подобия прямоугольных треугольников
- Прямоугольные треугольники
- Некоторые свойства прямоугольного треугольника:
- Соотношение между сторонами и углами в прямоугольном треугольнике:
- Значения тригонометрических функций некоторых углов:
- Прямоугольный треугольник
- 📸 Видео
Видео:16 фактов про ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК | ГеометрияСкачать

Определение
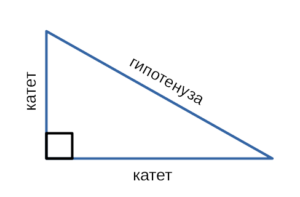
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.
Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.
Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Свойства прямоугольного треугольника
В прямоугольном треугольнике:
- Сумма острых углов 90˚.
- Катет, противолежащий углу в 30˚, равен половине гипотенузы.
- Медиана, проведенная к гипотенузе, равна ее половине.
- Центр описанной окружности — середина гипотенузы.
Формулы:
- Площадь прямоугольного треугольника равна
половине произведения катетов: - Радиус описанной окружности около прямоугольного
треугольника равен половине гипотенузы: - Радиус вписанной окружности в прямоугольный треугольник
выражается следующим образом: - Квадрат гипотенузы равен сумме квадратов катетов:
Видео:Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Признаки равенства прямоугольных треугольников
С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.
- По двум катетам:
Если два катета одного прямоугольного треугольника соответственно
равны двум катетам другого прямоугольного треугольника,
то такие треугольники равны. - По катету и гипотенузе:
Если катет и гипотенуза одного прямоугольного треугольника соответственно
равны катету и гипотенузе другого прямоугольного треугольника,
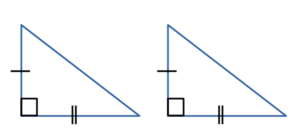
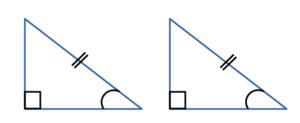
то такие треугольники равны. - По гипотенузе и острому углу:
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно
равны гипотенузе и острому углу другого прямоугольного треугольника,
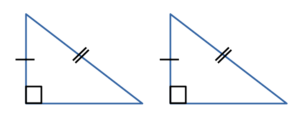
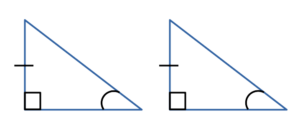
то такие треугольникиравны. - По катету и острому углу:
Если катет и острый угол одного прямоугольного треугольника соответственно
равны катету и острому углу другого прямоугольного треугольника,
то такие треугольники равны.
Видео:Все факты о медиане треугольника для ЕГЭСкачать

Признаки прямоугольного треугольника
С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.
- По теореме Пифагора:
Если квадрат стороны равен сумме квадратов двух других сторон,
то треугольник прямоугольный. - По центру описанной окружности:
Если центр описанной окружности лежит на стороне треугольника,
то треугольник прямоугольный. - По медиане:
Если медиана треугольника равна половине стороны, к которой она проведена,
то треугольник прямоугольный. - По площади:
Если площадь треугольника равна половине произведения двух его сторон,
то треугольник прямоугольный. - По радиусу описанной окружности:
Если радиус описанной окружности равен половине,
то треугольник прямоугольный.
Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Признаки подобия прямоугольных треугольников
С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.
Видео:Прямоугольный треугольник. Часть 3. Биссектриса | Борис Трушин #shortsСкачать

Прямоугольные треугольники
Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
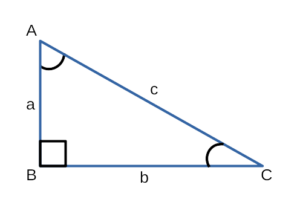
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $/$ | $/$ | $/$ |
| $cosα$ | $/$ | $/$ | $/$ |
| $tgα$ | $/$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $/$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√$. Найдите косинус внешнего угла при вершине $В$.
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
Катет $ВС$ мы можем найти по теореме Пифагора:
Подставим найденное значение в формулу косинуса
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA=/, AC=9$. Найдите $АВ$.
Распишем синус угла $А$ по определению:
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
Видео:Что с углами. Прямоугольный треугольник #shortsСкачать

Прямоугольный треугольник
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами .
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где
– катеты,
– гипотенуза. Видеодоказательство
4. Площадь прямоугольного треугольника с катетами
:
5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты
и гипотенузу
следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус описанной окружности есть половина гипотенузы
:
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус вписанной окружности выражается через катеты
и гипотенузу
следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
📸 Видео
Полезные факты про прямоугольный треугольник. Высота и медиана из прямого угла.Скачать

7 класс Прямоугольный треугольник. Важные фактыСкачать

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

3 правила про прямоугольный треугольник #SHORTSСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Прямоугольный треугольник. Свойства, доказательства.Скачать

Прямоугольный треугольник. Часть 1. Медиана | Борис Трушин #shortsСкачать

Виды треугольниковСкачать

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Прямоугольный треугольник Полное досьеСкачать

Секретное свойство прямоугольного треугольника! Только тссс🤫 #егэ2022 #треугольник #егэпоматематикеСкачать