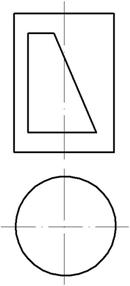
Построение окружности с вырезом (3 видео)

Построение вырезов на геометрических телах

Пример 1. Построить три проекции цилиндра с вырезом (рис. 147).

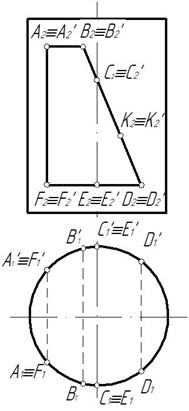
Отмечаем характерные точки выреза А, В, С, Д, Е, F, а также произвольную точку к для построения профильной проекции части эллипса. Горизонтальные проекции точек отмечаем на горизонтальном очерке цилиндра, так как горизонтальная проекция боковой поверхности цилиндра совпадает с горизонтальным очерком (рис .148)

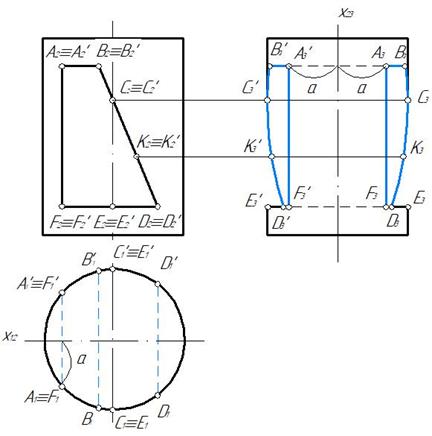
Построение профильной проекции выреза показано на рис. 149. Для этого целесообразно ось x ₁₂ провести через ось симметрии горизонтальной проекции,а ось x ₂₃ через профильную ось симметрии.

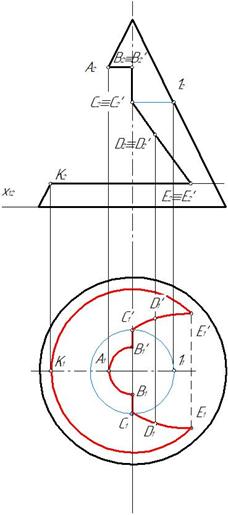
Пример 2. Построить три проекции конуса с вырезом (рис. 150).

Отмечаем характерные точки вареза А, В, С, Е, K, а также произвольную точку D для построения части эллипса. Горизонтальные проекции точек отмечаем на образующих конуса и вспомогательных окружностях (рис. 151).

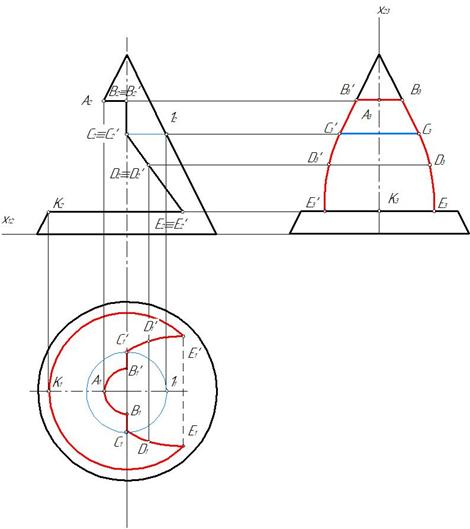
На рис. 152 показано построение профильной проекции конуса с вырезом.Для этого целесообразно ось x ₁₂ провести через ось симметрии горизонтальной проекции, а ось x ₂₃ через профильную ось симметрии.

Пример 3. Построить три проекции вырезе на призме (рис. 153).

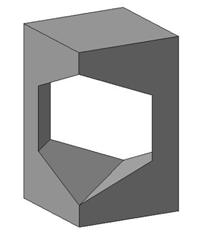
Решение показано на рис. 154

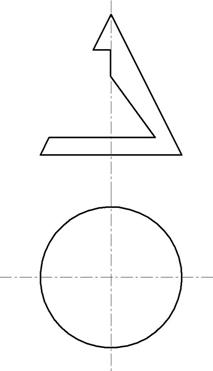
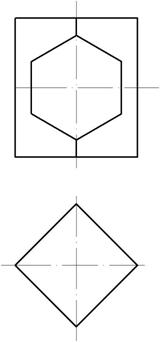
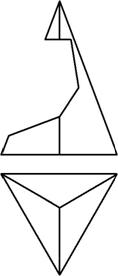
Пример 4. Построить три проекции выреза на пирамиде (рис. 155).

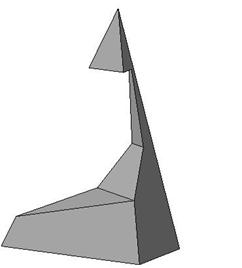
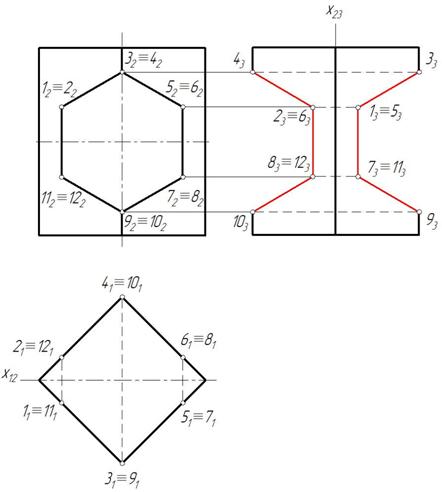
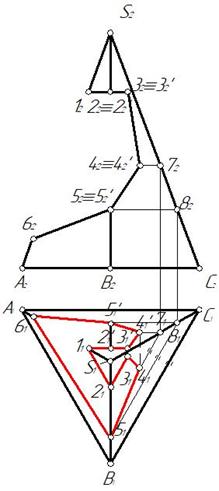
Отмечаем фронтальные проекции характерных точек выреза – это точки 1₂, 2₂, 3₂, 4₂, 5₂, 6₂. Для нахождения горизонтальных проекций точек 4 и 5 проводим по поверхности пирамиды две вспомогательные линии, параллельные основанию пирамиды ABC. Горизонтальные проекции этих линий являются треугольниками, параллельными горизонтальной проекции основания А₁В₁С₁. На этих треугольниках отмечаем горизонтальные проекции точек 4 и 5 (рис. 156).

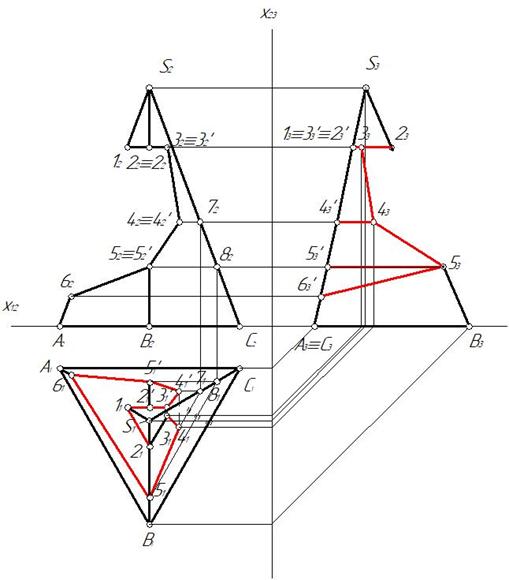
Затем строим профильную проекцию пирамиды и точек выреза. Для этого оси целесообразно провести как показано на рис. 157.

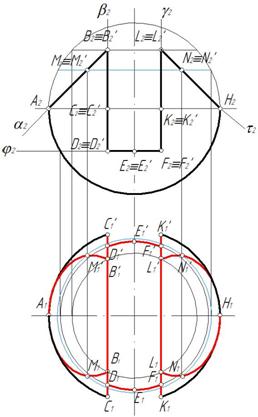
Пример 5. Построить три проекции выреза на сфере (рис. 158).

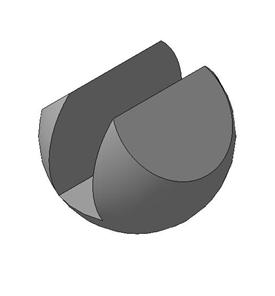
Вырез образован двумя фронтально-проецирующими плоскостями α и τ, горизонтальной плоскостью φ, двумя профильными плоскостями β и γ. Горизонтальная плоскость пересекает поверхность сферы по части окружности, ограниченной прямой. Фронтально-проецирующая плоскость пересекают поверхность сферы по окрухностям, которые на горизонтальной и профильной плоскости проецируются как части эллипсов. Профильная плоскость пересечет поверхность сферы по части окружности, которая на профильной плоскости спроецируется как часть окружности (рис. 159).

Построение профильной проекции показано на рис. 160

Содержание

ПОСТРОЕНИЕ ПРОЕКЦИЙ ТОЧЕК И ЧЕРТЕЖЕЙ ГЕОМЕТРИЧЕСКИХ ТЕЛ С ВЫРЕЗАМИ
Построение окружности с вырезом
Пошаговое руководство решения задачи №6 — построение линии пересечения сферической поверхности от сквозного призматического выреза.
🔥 Видео

Видео:Сечение сферыСкачать

ПОСТРОЕНИЕ ПРОЕКЦИЙ ТОЧЕК И ЧЕРТЕЖЕЙ ГЕОМЕТРИЧЕСКИХ ТЕЛ С ВЫРЕЗАМИ

В предыдущих параграфах было рассмотрено, что форма деталей состоит из сочетания различных геометрических тел. В деталях могут быть вырезы, срезы, отверстия.

Чтобы построить вырез на поверхности цилиндрической втулки, надо знать, как на цилиндрической поверхности найти проекции точек, принадлежащих этому вырезу.

Рассмотрим, как находят проекции точек на поверхностях геометрических тел.

1. Построение проекций точки, расположенной на поверхности призмы. Задана фронтальная проекция точки А»‘на видимой стороне поверхности призмы (рис. 3.10). Необходимо найти ее горизонтальную АТ’ и профильную К'» проекции. Чтобы найти горизонтальную проекцию точки, спроецируем ее на соответствующую грань горизонтальной проекции призмы. Затем через заданную точку на виде спереди К» проводим линию проекционной связи на вид слева, а с вида сверху точку К спроецируем по линиям связи на постоянную прямую и вид слева. При взаимном пересечении линии связи находим проекцию точки на виде слева.
2. Построение проекций точки, расположенной на поверхности цилиндра. Задана фронтальная проекция К» точки К на видимой стороне поверхности цилиндра (рис. 3.11). Необходимо найти ее горизонтальную и профильную проекции. Боковая поверхность цилиндра проецируется на горизонтальную плоскость проекций в окружность.

Заданная точка лежит на боковой поверхности цилиндра и, естественно, на горизонтальной проекции спроецируется на эту окружность. Профильная проекция К»‘ заданной точки будет лежать на горизонтальной прямой, проведенной из точки К».

Расстояние от оси цилиндра до искомой точки находим по линиям проекционной связи с вида сверху.

3. Построение проекций точки, расположенной на поверхности пирамиды. Задана фронтальная проекция точки А»‘на видимой стороне поверхности пирамиды (рис. 3.12, а). Необходимо найти ее горизонтальную АТ’и профильную АТ'» проекции. Возможны два решения.

А. Соединим вспомогательной прямой заданную проекцию точки К’ с проекцией вершины пирамиды S и продлим эту прямую до пересечения с основанием.

Находим проекцию проведенной прямой S’А’ на виде сверху. Для этого точку пересечения А спроецируем на основание горизонтальной проекции пирамиды А’ и соединим ее с проекцией вершины s.

Горизонтальную проекцию точки К найдем, спроецировав заданную проекцию точки К’ на проведенную линию A’S’.

Б. Проведем через точку К» секущую плоскость Р (рис. 3.11,6).

Пирамида превращается как бы в усеченную. По линиям проекционной связи находим проекцию точки на виде сверху и слева.

4, Построение проекций точки, расположенной на поверхности конуса. Задана фронтальная проекция точки К» на видимой стороне поверхности конуса (рис. 3.13). Необходимо найти ее горизонтальную К и профильную К'» проекции. Возможны два решения.

А. Через заданную проекцию точки К» проведем линию, параллельную основанию конуса (рис. 3.13, а). Она спроецируется на горизонтальную проекцию в окружность, диаметр которой будет равен диаметру конуса в этом месте. Пересечение линии связи с этой окружностью даст горизонтальную проекцию точки К’. Затем по линиям проекционной связи находим ее изображение на виде слева.

Б. На виде спереди (рис. 3.13, б) через вершину конуса и заданную точку К» проводим образующую и отмечаем на основании конуса точку А» — пересечение образующей с основанием. При помощи линии связи находим на основании ее горизонтальную проекцию образующей конуса. Горизонтальная проекция точки JC будет лежать на горизонтальной проекции образующей в пересечении ее с линией связи. По линиям проекционной связи находим ее проекцию на виде слева.

5. Построение проекций точки, расположенной на поверхности шара. Задана фронтальная проекция точки К» на видимой стороне поверхности шара (рис. 3.14). Найдем ее горизонтальную К и профильную К'» проекции. Через заданную точку проведем параллель, она спроецируется на горизонтальной проекции шара в окружность,

диаметр которой равен диаметру окружности шара на высоте заданной точки. Спроецируем на нее заданную точку и получим искомую горизонтальную проекцию К. Профильная проекция заданной точки находится по общим правилам прямоугольного проецирования.

Видео:Построение недостающих проекции сквозного отверстия в сфереСкачать

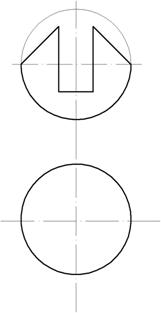
Построение окружности с вырезом

Видео:СФЕРА с вырезомСкачать

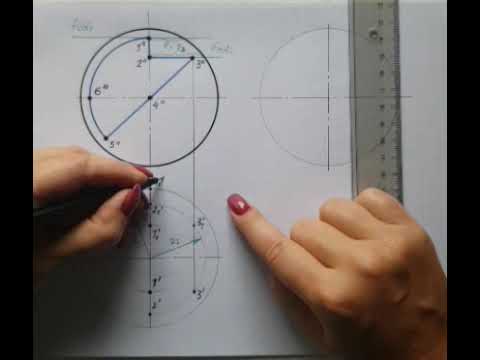
Пошаговое руководство решения задачи №6 — построение линии пересечения сферической поверхности от сквозного призматического выреза.

Необходимо построить линию пересечения сферической поверхности (шара) от сквозного призматического выреза, состоящего из четырех граней (проецирующих плоскостей). Фронтальная проекция линии пересечения заданных поверхностей (шара и многогранника) задана исходным чертежом, требуется построить ее в горизонтальную и профильную проекции.

Для решения такой задачи по начертательной геометрии необходимо знать:

— построение трех проекций сферической поверхности (шара) по заданным координатам, на комплексном чертеже;

— построение линии пересечения шаровой поверхности с гранным телом;

— частные случаи построения линии пересечения шаровой поверхности с проецирующей плоскостью.

Порядок решения Задачи

Рис.6.1

1. В правой части листа формата A3 наносятся оси координат и согласно варианту задания строится фронтальная, горизонтальная и профильная проекции сферы (шара) заданного радиуса.

По координатам точек, взятым из таблицы по своему варианту, наносятся вершины сквозного четырехгранного выреза во фронтальной проекции (рис.6.1).

2. Решение задачи заключается в построении горизонтальной и профильной проекции линии пересечения данного выреза.

Прежде чем приступить к построению этих проекций, необходимо вспомнить некоторые частные случаи сечений шаровой поверхности от проецирующей плоскости (сквозное отверстие можно рассматривать как гранное тело, образованное четырьмя плоскостями), а именно:

(а) если плоскость во фронтальной проекции рассекает шаровую поверхность параллельно экватору, то в горизонтальной проекции это сечение проецируется в виде окружности с радиусом, взятым в этом сечении от оси вращения шара до очерка, а в профильной проекции это сечение проецируется в виде прямой линии;

(b) если плоскость во фронтальной проекции рассекает шаровую поверхность перпендикулярно экватору, то в горизонтальной проекции это сечение проецируется в виде прямой линии, а в профильной — в виде окружности с радиусом, взятым тем же способом что и в первом случае;

(c) если плоскость во фронтальной проекции рассекает шаровую поверхность под некоторым (отличным от 0 и 90 градусов) углом к экватору, то в горизонтальной и фронтальной проекциях это сечение будет проецироваться в виде эллипса. Построение эллипса осуществляется по опорным (характерным) и некоторым промежуточным, взятым произвольно, точкам;

(d) все точки фронтальной проекции сферы, расположенные на очерке, в горизонтальной проекции будут проецироваться на экваторе, а в профильной — на главном меридиане;

(e) все точки фронтальной проекции сферы, расположенные на экваторе, в горизонтальной проекции будут проецироваться на очерке, а в профильной — на экваторе;

(f) все точки фронтальной проекции сферы, расположенные на главном меридиане, в горизонтальной проекции будут проецироваться также на главном меридиане, а в профильной — на очерке сферы.

Рис.6.2

3. С учетом приведенных частных случаев сечений построение выреза в горизонтальной и профильной проекциях не вызывает особых затруднений и начинается с определения характерных (опорных) точек сквозного выреза во фронтальной проекции. Этими точками являются А, В, С, D. Тогда берем проекцию стороны призмы B’C’ и рассматриваем ее как проецирующую плоскость ’, рассекающую шар параллельно экватору, — строим в горизонтальной проекции окружность с радиусом r₁ взятым в этой плоскости, от оси шара до очерка. Проецируем на эту окружность точки B’ и C’, получаем B и C — их горизонтальные проекции. Вполне очевидно, что этих точек будет по две (точки входа и выхода), т.к. отверстие сквозное.

Аналогичным способом строится проекция сечения плоскости А’D’. Берется радиус от оси сферы до очерка (разумеется не до точки A’) и в горизонтальной проекции проводится окружность этим радиусом. Проецированием находятся проекции точек D (их будет две — точка входа и точка выхода) — D и D₁ и промежуточной точки, расположенной на экваторе.

Рис.6.3

Сторона четырехугольника СD горизонтальной проекции проецируется в прямую линию, причем эта линия должна начинаться от очерка, т.к. во фронтальной проекции
она пересекает экватор шара и продолжается до точек С и D.

Рис.6.4

Горизонтальной проекцией сторон четырехугольника АВ будет эллипс, строим его по характерным (опорным) точкам. Проецируем точки, расположенные на меридиане, экваторе и очерке фронтальной проекции соответственно на меридиан, очерк и экватор горизонтальной проекции. Соединяя их по лекалу с уже имеющимися
проекциями точек B и B₁, и получаем искомую проекцию эллипса.

4. Аналогичным способом строится третья профильная проекция данного выреза (вид слева), поэтому нет надобности в подробном изложении четырехугольника ВС и АD будут проецироваться в прямые линии, СD – в окружность, AB – в эллипс.

Рис.6.5

5. Заключительным этапом в решении задачи является определение видимости сторон сквозного выреза, которая определяется из расположения их на сопряженной плоскости проекций. Тогда видимыми точками и линиями в горизонтальной плоскости будут точки и линии, которые во фронтальной — расположены выше экватора и на профильной проекции видимыми будут точки и линии которые на фронтальной плоскости расположены левее меридианы.

Экватор и меридиан являются границами видимости. Точки и линии, расположенные ниже экватора и правее меридиана во фронтальной проекции, в горизонтальной и профильной проекциях будут невидимыми.