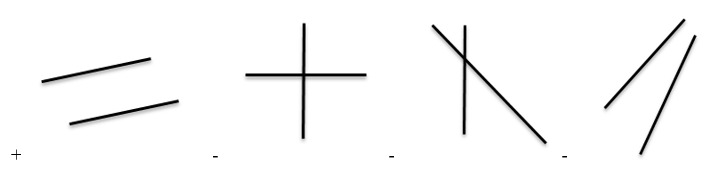Тест по теме параллельные прямые в пространстве 10 класс с ответами

Тесты по геометрии 10 класс. Тема: «Параллельные прямые в пространстве»

Правильный вариант ответа отмечен знаком +

1. Выберите вариант ответа, в котором представлена правильная теория?

— Через две параллельные прямые возможно провести лишь две плоскости.

+ Через две параллельные прямые проходит лишь одна плоскость.

— Через множество параллельных прямых невозможно провести одну плоскость.

— Через две параллельные между собой прямые проходят три плоскости.

2. Каким знаком отмечают параллельность?

3. Какие прямые именуются параллельными в пространстве?

— находящиеся в одной плоскости и обладающие двумя точками пересечения.

— принадлежащие одной плоскости и обладающие одной точкой пересечения.

+ принадлежащие одной плоскости и не имеющие общих точек пересечения.

— принадлежащие двум плоскостям и представляющие собой перпендикулярные прямые.

4. В каком варианте ответа представлено правильное утверждение?

— Когда точка G принадлежит данной прямой, через нее можно провести две прямые, параллельные данной прямой.

— Когда точка N не принадлежит данной прямой, через нее проходят две прямые, перпендикулярные данной прямой.

+ Когда точка Q не лежит на данной прямой, через нее проходит единственная прямая, параллельная данной прямой.

— Когда точка H не находится на данной прямой, через нее нельзя провести прямую, параллельную данной прямой.

5. Выберите вариант ответа, в котором представлены две параллельные прямые:

6. Что такое параллельный пучок прямых?

— Это множество скрещивающихся прямых в пространстве.

+ Это множество прямых в пространстве, параллельных данной прямой.

— Это любые десять прямых в пространстве.

— Это множество прямых в пространстве, перпендикулярных данной прямой.

7. Выберите ошибочное суждение:

+ Даны три прямые. Первая прямая K параллельна второй прямой M, вторая прямая M – третьей прямой N. Из данного следует, что первая и третья прямые K и N именуются не параллельными, а перпендикулярными.

— Если взять любые две прямые пучка параллельных прямых, то они окажутся параллельными между собой.

— Параллельному пучку прямых характерно свойство транзитивности.

— Когда прямая K является параллельной прямой M, прямая M – прямой N, тогда прямые K и N также являются параллельными.

8. Каким образом маркируется параллельность двух прямых K и M?

9. Даны три прямые P, S, T. Если первая прямая P является параллельной второй прямой S, а третья прямая T – параллельной первой прямой P, то:

+ вторая и третья прямые S и T являются параллельными.

— прямая S является перпендикулярной прямой T.

— прямым S и T характерна лишь одна точка пересечения.

— через прямые S и T будут проходить две плоскости.

тест 10. В каком варианте ответа указано правильное суждение о параллельности прямых в пространстве:

— Если взять любые три прямые, пересекающиеся между собой и в то же время находящиеся в одной плоскости, то они будут именоваться параллельными в пространстве.

— При условии, что две прямые лежат в двух разных плоскостях и не обладают общими точками пересечения, их именуют параллельными в пространстве.

+ Три прямые будут представлять собой параллельные прямые, если они будут перпендикулярны одной и той же плоскости.

— Три прямые являются параллельными, если они не перпендикулярны одной и той же плоскости.

11. Как именуются не обладающие общей точкой пересечения прямые, через которых нельзя провести плоскость?

12. Если пять отрезков находятся на пяти параллельных прямых, то они представляют собой:

13. Сколько параллельных прямых возможно провести через любую точку пространства, которая находится вне данной прямой?

14. В каком варианте представлена безошибочная теория?

+ Если данная плоскость пересекает одну из трех параллельных прямых, то она пересекается и с остальными двумя прямыми.

— Когда два из трех параллельных прямых пересекают данную плоскость, то третья прямая пересекает перпендикулярную ей плоскость.

— Две параллельные прямые всегда пересекаются с двумя разными плоскостями.

— Две параллельные прямые никогда не пересекаются с плоскостью.

15. Прямых называют скрещивающимися, если они:

+ не принадлежат одной плоскости.

— находятся в одной плоскости.

— не имеет точек пересечения.

— никогда не пересекаются.

16. Выберите вариант ответа, в котором указано правильное суждение о параллельности прямых в пространстве:

+ Если три отрезка параллельны между собой, то прямые, на которых они находятся, также являются параллельными.

— Когда два отрезка параллельны между собой, то прямые, на которых они лежат, не являются параллельными.

— Если два отрезка пересекаются между собой, то прямые, на которых они лежат, являются параллельными.

— Если два отрезка перпендикулярны, то прямые, на которых они лежат, являются параллельными.

17. В каком варианте правильно указана параллельность прямых d и c?

18. Прямая и плоскость именуются параллельными, когда они:

— обладают одну общую точку.

— имеют точку пересечения.

— характеризуются двумя общими точками.

+ не обладают общих точек.

19. Если плоскость и прямая характеризуются только одной общей точкой, то это значит, что они:

тест-20. Дан параллелепипед ABCDA1B1C1D1. Какие прямые здесь являются параллельными?

21. Даны две параллельные прямые в простанстве. Одна из них является параллельной к третьей прямой. Выберите вариант ответа, в котором представлено ошибочное суждение:

+ Первая, вторая прямые перпендикулярны к третьей.

— Первая прямая параллельна второй.

— Вторая и третья прямые являются параллельными.

— Три прямые не имеют точек пересечения.

22. Дан параллелепипед ABCDA1B1C1D1. Являются ли параллельными прямые АВ и CD?

— зависят от объема параллелепипеда

— зависят от площади параллелепипеда

23. Две прямые пересекаются. Из данного следует, что:

— они обладают двумя общими точками.

— они принадлежат одной плоскости.

+ они обладают одной общей точкой.

— они не имеют общих точек.

24. Дан куб ABCDA1B1C1D1. Прямые СС1 и DD1:

— имеют одну точку пересечения

25. У двух прямых отсутствует общих точек, из этого следует, что они являются:

26. Выберите верное утверждение:

— Трем параллельным прямым в пространстве присущи три точки пересечения.

+ Десять параллельных прямых в пространстве никогда не будут пересекаться.

— Когда одна прямая параллельна четырем другим параллельным прямым, то это значит, что они пересекаются в четырех точках.

— Две параллельные прямые в пространстве характеризуются перпендикулярностью.

27. Дан куб ABCDA1B1C1D1. Указанные в каком варианте прямые не являются параллельными?

28. В каком варианте представлен правильный вариант теории?

— Две прямые именуются перпендикулярными, когда они являются параллельными третьей прямой.

— Две прямые именуются прямыми, когда они являются параллельными третьей прямой.

-Две прямые именуются скрещивающимися, когда они являются параллельными третьей прямой.

+ Когда две прямые являются параллельными третьей прямой, их именуют параллельными.

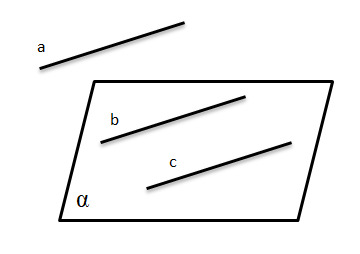
29. Посмотрите на рисунок и выберите вариант ответа, в котором указано ошибочное суждение.

— Прямые b и c никогда не будут иметь общих точек пересечения.

— Прямая b принадлежит плоскости α.

+ прямые a и cпредставляют собой не параллельные прямые.

— прямые a, bи cхарактеризуются параллельностью.

тест_30. Дан параллелепипед ABCDA1B1C1D1. Указанные в каком варианте прямые не являются параллельными?

Видео:10 класс - Геометрия - Параллельные прямые в пространстве. Параллельность трёх прямыхСкачать

Г10(I)-1. Параллельность прямых, прямой и плоскости

Геометрия. 10 класс. Глава I. Тест 1.

Вариант 1.

1. Выбрать верное утверждение.

1) Две прямые в пространстве называются параллельными, если они не пересекаются.

2) Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.

3) Если прямая параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна этой плоскости.

4) Через любую точку пространства проходит прямая, параллельная данной прямой, и притом только одна.

A) 1; B) 4; C) 3; D) 2.

2. Какой из чертежей на рисунке 1 может служить иллюстрацией следующего утверждения: если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость?

A) б); B) а); C) в); D) г).

3. На рисунке 2 точки E, F, P и K –середины отрезков АС, АМ, ВМ и ВС. Найти периметр четырёхугольника EFPK,

если МС=21 см, АВ=13 см.

A) 8 см; B) 34 см; C) 17 см; D) 68 см.

4. Сторона АС треугольника АВС лежит в плоскости α. МϵАВ, NϵBC, MN||α, причём BM:AM=2:7, MN=6 см. Сделать чертёж. Найти АС.

A) 18 см; B) 30 см; C) 27 см; D) 36 см.

Вариант 2.

1. Выбрать верное утверждение.

1) Если плоскость проходит через прямую, параллельную другой плоскости, то эти плоскости будут параллельны.

2) Если две прямые параллельны третьей прямой, то они перпендикулярны.

3) Если прямая параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна данной плоскости.

4) Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

A) 1; B) 4; C) 3; D) 2.

2. Какой из чертежей на рисунке 1 может служить иллюстрацией следующего утверждения: через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна?

A) б); B) а); C) в); D) г).

3. На рисунке 2 точки F, P, Q и N –середины отрезков АB, АМ, CМ и ВС. Найти периметр четырёхугольника FPQN, если AС=17 см, ВM=25 см.

A) 32 см; B) 21 см; C) 42 см; D) 84 см.

4. Плоскость α параллельна стороне АС треугольника АВС и пересекает стороны АВ и ВС в точках К и F соответственно, BF:FC=5:6, АС=22 см. Сделать чертёж. Найти KF.

A) 15 см; B) 9 см; C) 10 см; D) 12 см.

Вариант 3.

1. Выбрать верные утверждения.

1) Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

2) Если параллельные прямые а и b лежат в плоскости α, то и прямая с, пересекающая прямые а и b, лежит в плоскости α.

3) Если средняя линия трапеции лежит в плоскости α, то прямые, содержащие её основания пересекут плоскость α.

A) 1); 2); 3); B) 1); 3); C) 1); 2); D) 2); 3).

2. Каким чертежом (какими чертежами) на рисунке 1 можно проиллюстрировать следующее утверждение.

Возможны три случая взаимного расположения прямой и плоскости: а) прямая и плоскость имеют только одну общую точку; б) прямая лежит в плоскости; в) прямая и плоскость не имеют ни одной общей точки.

А) б); в); B) а); б); г); C) б); в); г); D) а).

3. На рисунке 2 точки E, F, P и K – середины отрезков АС, АМ, ВМ и ВС. Периметр четырёхугольника EFPK равен 32 см, причём разность длин любых его смежных сторон составляет 2 см. Найти МС и АВ (МС

A) MC=14 см; AB=18 см; B) MC=15 см; AB=17 см;

C) MC=12 см; AB=20 см; D) MC=10 см; AB=22 см.

4. Отрезок АВ пересекает плоскость α в точке О. Точка С – середина отрезка ОВ. Параллельные прямые, проведённые из точек А, В и С к плоскости α, пересекают её в точках А₁, В₁ и С₁ соответственно. АА₁=6 см, А₁О:ОС₁=1:3. Сделать чертёж. Найти ВВ₁.

A) 18 см; B) 30 см; C) 32 см; D) 36 см.

Вариант 4.

1. Выбрать верные утверждения.

1) Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

2) Возможны три случая взаимного расположения прямой и плоскости: а) прямая лежит в плоскости; б) прямая и плоскость пересекаются; в) прямая и плоскость параллельны.

3) Если стороны MN и NP параллелограмма MNPQ пересекают плоскость α, то и прямые MQ и PQ пересекут эту плоскость.

A) 1); 2); 3); B) 1); 3); C) 1); 2); D) 2); 3).

2. Каким чертежом (какими чертежами) на рисунке 1 можно проиллюстрировать следующее утверждение.

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

А) б); в); B) а); C) а); б); D) а); г).

3. На рисунке 2 точки F, P, Q и N – середины отрезков АB, АМ, CМ и ВС. Периметр четырёхугольника FPQN равен 38 см, причём разность длин любых его смежных сторон составляет 3 см. Найти AС и BM (AС

Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Тест по теме «Параллельность прямых и плоскостей в пространстве» С ОТВЕТАМИ 10 кл

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Тест по теме «Параллельность прямых и плоскостей в пространстве»

1. Пересечением двух плоскостей является

А) точка Б) прямая В) отрезок

2. Сколько должно быть общих точек у прямой с плоскостью, чтобы она лежала в этой плоскости?

А) одна Б) две В) три

3. На сколько множеств разбивает пространство любая плоскость?

А) на два Б) на три В) на четыре

4. Чтобы задать единственную плоскость необходимо

А) две точки Б) три точки

В) три точки, не лежащие на одной прямой

5. Какие из перечисленных фигур задают единственную плоскость в пространстве?

А) две параллельные прямые

Б) две скрещивающиеся прямые

6. Сколько плоскостей задают две пересекающиеся прямые?

А) одну плоскость

Б) две плоскости

В) бесконечно много плоскостей

7. Через какие из перечисленных фигуры можно провести единственную плоскость?

А) Через три точки

Б) Через прямую и не лежащую на ней точку

В) Через отрезок

8. Две прямые пересекаются. Что это значит?

А) Они имеют две общие точки.

Б) Они имеют одну общую точку.

В) Они лежат в одной плоскости.

9. Две прямые называются скрещивающимися, если

А) они не имеют общих точек и не лежат в одной плоскости.

Б) они не имеют общих точек.

В) они имеют одну общую точку.

10. Две прямые в пространстве называются параллельными, если

А) они не имеют общих точек.

Б) они не имеют общих точек и лежат в одной плоскости. В) они не имеют общих точек, и не существует проходящей через них плоскости.

11. Прямая и плоскость не имеют общих точек. Это значит, что

А) они параллельны.

Б) они пересекаются.

В) они скрещиваются.

12. Прямая и плоскость имеют только одну общую точку. Это значит, что

А) они параллельны.

Б) они пересекаются.

В) они скрещиваются.

13. Если две плоскости не имеют общих точек, то они

14. Две плоскости пересекаются. Это значит, что

А) они имеют одну общую точку.

Б) они имеют общую прямую.

В) они имеют общий луч.

15. Укажите свойства параллельных плоскостей

А) Две прямые параллельные третьей прямой, параллельны

Б) Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

В) Отрезки параллельных прямых, заключенные между двумя параллельными

16. Прямолинейные отрезки фигуры изображаются на плоскости чертежа

17. Укажите признак параллельности прямой и плоскости

А) Две прямые параллельные третьей прямой, параллельны

Б) Если две пересекающиеся прямые одной плоскости соответственно параллельны

двум прямым другой плоскости, то эти плоскости параллельны.

В) Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой

в этой плоскости, то она параллельна и самой плоскости.

Тест по теме: «Параллельность прямых и плоскостей в пространстве»

1. Сколько должно быть общих точек у прямой с плоскостью, чтобы она лежала в этой плоскости?

А) одна Б) две В) три

2. Что является пересечением двух плоскостей

А) прямая Б) отрезок В) точка

3. На сколько множеств разбивает пространство любая плоскость?

А) на три Б) на четыре В) на два

4. Сколько плоскостей задают две пересекающиеся прямые?

А) две плоскости

Б) одну плоскость

В) бесконечно много плоскостей

5. Какие из перечисленных фигур задают единственную плоскость в пространстве?

Б) две скрещивающиеся прямые

В) две параллельные прямые

6. Чтобы задать единственную плоскость необходимо

А) две точки Б) три точки

В) три точки, не лежащие на одной прямой

7. Через какие из перечисленных фигуры можно провести единственную плоскость?

А) Через три точки

Б) Через прямую и не лежащую на ней точку

В) Через отрезок

8. Две плоскости пересекаются. Это значит, что

А) они имеют одну общую точку.

Б) они имеют общую прямую.

В) они имеют общий луч.

9. Две прямые называются скрещивающимися, если

А) они не имеют общих точек и не лежат в одной плоскости.

Б) они не имеют общих точек.

В) они имеют одну общую точку.

10. Две прямые в пространстве называются параллельными, если

А) они не имеют общих точек.

Б) они не имеют общих точек и лежат в одной плоскости. В) они не имеют общих точек, и не существует проходящей через них плоскости.

11. Прямая и плоскость не имеют общих точек. Это значит, что

А) они параллельны.

Б) они пересекаются.

В) они скрещиваются.

12. Свойства параллельных плоскостей

А) Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

Б) Две прямые параллельные третьей прямой, параллельны

В) Отрезки параллельных прямых, заключенные между двумя параллельными

13. Прямая и плоскость имеют только одну общую точку. Это значит, что

А) они параллельны.

Б) они пересекаются.

В) они скрещиваются.

14. Две прямые пересекаются. Что это значит?

А) Они имеют две общие точки.

Б) Они лежат в одной плоскости.

В) Они имеют одну общую точку.

15. Если две плоскости не имеют общих точек, то они

16. Прямолинейные отрезки фигуры изображаются на плоскости чертежа

17. Укажите признак параллельности плоскостей

А) Две прямые параллельные третьей прямой, параллельны

Б) Если две пересекающиеся прямые одной плоскости соответственно параллельны

двум прямым другой плоскости, то эти плоскости параллельны.

В) Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой

в этой плоскости, то она параллельна и самой плоскости.

Указать прямые, параллельные прямой

Видео:Параллельность прямых. 10 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 340 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Тасимова Айгуль ДжанбулатовнаНаписать 62734 18.11.2017

Номер материала: ДБ-879102

18.11.2017 841

16.11.2017 649

15.11.2017 366

14.11.2017 1306

13.11.2017 310

13.11.2017 312

12.11.2017 963

12.11.2017 242

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России разработают рекомендации по сопровождению студентов с ОВЗ

Время чтения: 2 минуты

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📹 Видео

Геометрия 10 класс. Тема: Параллельные прямые в пространстве. (Л.С. Атанасян)Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельность прямой и плоскости. 10 класс.Скачать

НАСКОЛЬКО СТАР ВАШ МОЗГ? Удивительный тест на эрудицию и общие знания #насколькотыумный #эрудицияСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

Параллельность прямых. Практическая часть. 10 класс.Скачать

4. Параллельные прямые в пространствеСкачать

Параллельные прямые в пространствеСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Геометрия 10 класс Параллельность прямых, прямой и плоскости теорияСкачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

10 класс, 15 урок, Перпендикулярные прямые в пространствеСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Параллельные прямые. Видеоурок 2. Геометрия 10 классСкачать

Видеоурок "Параллельные прямые в пространстве"Скачать