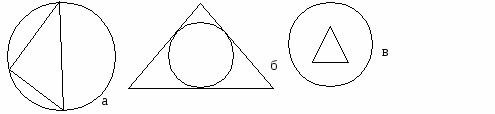Тест описанная окружность 8 класс атанасян

Цель данного теста – проверить уровень усвоения теоретического материала по данной теме.

Просмотр содержимого документа
«Тест по теме » Вписанная и описанная окружности» по геометрии 8 класс»

Муниципальное бюджетное общеобразовательное учреждение

« Выделянская средняя общеоразовательная школа»

Родионово-Несветайского района Ростовской области

Лященко Людмила Егоровна, учитель математики и биологии

Тест по теме «Вписанная и описанная окружности»

Цель данного теста – проверить уровень усвоения теоретического материала по данной теме.

Тест по теме «Вписанная и описанная окружности».

1. Каждая точка биссектрисы неразвернутого угла равноудалена от его

а) углов; б) сторон; в) вершин.

2. Каждая точка серединного перпендикуляра к отрезку

а) равноудалена от концов этого отрезка;

б) равноудалена от середины этого отрезка;

в) равноудалена от углов.

3. Если все стороны многоугольника касаются окружности, то окружность называется

а) описанной около многоугольника;

б) вписанной в треугольник;

в) вписанной в многоугольник.

4. В любой треугольник можно вписать только

а) две окружности;

б) три окружности

в) одну окружность.

5. В любом вписанном четырехугольнике сумма противолежащих углов равна

а) 360 0 ; б) 180 0 ; в) 90 0 .

6. Центр вписанной окружности лежит в точке пересечения

б) серединных перпендикуляров;

7. Описанная около треугольника окружность изображена на рисунке:

8. Вписанная в четырехугольник окружность изображена на рисунке:

Тест по теме «Вписанная и описанная окружности».

1. Каждая точка, равноудаленная от сторон угла, лежит на его

а) медиане; б) высоте; в) биссектрисе.

2. Серединным перпендикуляром к отрезку называется прямая,

а) проходящая через середину данного отрезка и перпендикулярная к нему;

б) проходящая через середину данного отрезка;

в) перпендикулярная к отрезку.

3. Если все вершины многоугольника лежат на окружности, то окружность называется

а) описанной около многоугольника;

б) описанной около треугольника;

в) вписанной в многоугольник.

4. Около любого треугольника можно описать только

а) две окружности;

б) одну окружность;

в) три окружности.

5. В любом описанном четырехугольнике суммы противолежащих сторон

а) равны; б) равны радиусу; в) равны периметру.

6. Центр описанной окружности лежит в точке пересечения

б) серединных перпендикуляров;

7. Вписанная в треугольник окружность изображена на рисунке:

8. Описанная около четырехугольника окружность изображена на рисунке:

I вариант 1б; 2а; 3в; 4в; 5б; 6в; 7а; 8б.

II вариант 1в; 2а; 3а; 4б; 5а; 6б; 7б; 8в.

Л.С. Атанасян, В.Ф. Бутузов и др. «Геометрия 7-9», учебник для общеобразовательных учреждений, Москва, «Просвещение», 2012 г.

Н.Ф. Гаврилова «Поурочные разработки по геометрии 8 класс», Москва, «ВАКО», 2006 г.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Тест по теме » Вписанная и описанная окружность »
тест по геометрии (8 класс) на тему

Данный тест проверяет знания учащихся по теме » Вписанная и описанная окружности»

Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Скачать:

Хочешь подготовиться к ЕГЭ за 1450 ₽ в месяц?

Вебинары Учи.Дома помогут подготовиться к ЕГЭ 2022. Поддерживающее коммьюнити из классных преподавателей, которые состоят в комиссии и знают особенности заданий изнутри. Хочешь попробовать бесплатно? Кликай по кнопке!

попробовать бесплатно, онлайн, 40 минут

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Предварительный просмотр:

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

• Биссектрис треугольника
• Высот треугольника
• Медиан треугольника
• Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

• AB+BC=AD+CD; — AB+CD=BC+AD;
• AB+AD=BC+CD; — AD·BC=AB·CD .

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

• Высот треугольника
• Серединных перпендикуляров к сторонам треугольника
• Биссектрис треугольника
• Медиан треугольника.

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

• ; — AB+CD=BC+AD;
• ; — AD·BC=AB·CD .

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Видео:8 класс, 38 урок, Вписанная окружностьСкачать

По теме: методические разработки, презентации и конспекты

Урок геометрии в 8 классе по теме «Вписанная и описанная окружность»

Презентация к уроку включает определения основных понятий, создание проблемной ситуации, а также развитие творческих способностей учащихся.

Лабораторная работа по теме «Вписанные и описанные окружности»

Исследуем вопрос об окружностях для треугольников, четырехугольников и правильных многоугольников.

Лабораторная работа по теме «Вписанные и описанные окружности»

Карточка — организатор деятельности по изучению или обобщению темы. Такая работа позволяет анализировать сходства и различия, упрощает понимание и запоминание.

Элективный курс по теме «Вписанные и описанные окружности» для учащихся основной школы

Элективные курсы – это обязательные для посещения курсы по выбору учащихся, входящие в состав профиля обучения на старшей ступени школы.Выполняя функцию внутрипрофильной специализации обучения, электи.

Диктант по геометрии в 8 классе. Тема » Вписанные и описанные окружности»

Диктант можно использовать на уроке систематизации знаний перед контрольной работой. Вопросы диктанта появляются по щелчку левой мыши.

Конспект урока геометрии 8 класс по теме: «Вписанная и описанная окружность» Атанасян.

Конспект урока геометрии 8 класса по теме: «Вписанная и описанная окружность» автор учебника Атанасян.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

Тест по теме: «Вписанная и описанная окружности» (8 класс).

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Тест по геометрии на тему: «Описанная окружность» 8 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:8 класс, 39 урок, Описанная окружностьСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Описанная окружность.docx

Тест по геометрии «Описанная окружность»

Если все вершины многоугольника лежат на окружности, то окружность называется _____________ около этого многоугольника, а многоугольник _________________ в эту окружность

Если сумма противоположных углов четырехугольника равна 180 о , то ___________________ можно ____________ окружность.

3. Около какого треугольника можно описать окружность?

г) все варианты верны

4. Сколько окружностей можно описать около треугольника:

г) Не в любой треугольник можно вписать окружность

5. Центром описанной около треугольника окружности является точка пересечения:

а) Биссектрис треугольника

б) Высот треугольника

в) Медиан треугольника

г) Серединных перпендикуляров к сторонам треугольника.

6. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

а); в) AB + CD = BC + AD ;

б ) ; г ) AD·BC=AB·CD .

7. Описанная около четырехугольника окружность изображена на рисунке:

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 325 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 698 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 483 436 материалов в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

75. Описанная окружность

Видео:Геометрия 8 класс (Урок№33 - Описанная окружность.)Скачать

Дистанционные курсы для педагогов

Другие материалы

• 16.05.2018
• 1220

• 16.05.2018
• 378

• 16.05.2018
• 1135

• 16.05.2018
• 1529

• 16.05.2018
• 2468

• 16.05.2018
• 528

• 16.05.2018
• 313

• 16.05.2018
• 635

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 16.05.2018 1033 —> —> —> —>
• RAR 16.9 кбайт —> —>
• Оцените материал:

Настоящий материал опубликован пользователем Кирякова Марина Леонидовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 10 месяцев
• Подписчики: 0
• Всего просмотров: 78272
• Всего материалов: 64

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Урок по теме ОПИСАННАЯ ОКРУЖНОСТЬ 8 классСкачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Петербурге дали рекомендации по переводу школьников на дистант

Время чтения: 3 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Якутске все классы, кроме девятых и одиннадцатых, перейдут на удаленку

Время чтения: 1 минута

Федеральный перечень учебников будет дополнен новыми учебниками

Время чтения: 3 минуты

В местах сдачи ЕГЭ будут применены антиковидные меры

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🌟 Видео

Окружность вписанная в треугольник и описанная около треугольника.Скачать

ВПИСАННАЯ ОКРУЖНОСТЬ радиус 8 класс АтанасянСкачать

Урок по теме ВПИСАННАЯ ОКРУЖНОСТЬСкачать

ВПИСАННАЯ окружность ОПИСАННАЯ окружность радиус 8 классСкачать

Вписанная окружность. Видеоурок по геометрии 8 классСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

ГЕОМЕТРИЯ 8 класс: Решение задач. Описанная окружностьСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Описанная окружность. Видеоурок 22. Геометрия 8 классСкачать

ВСЯ ГЕОМЕТРИЯ 8 КЛАСС ЗА 15 МИНУТ / АТАНАСЯН / К ОГЭСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать