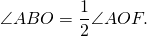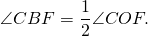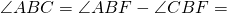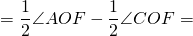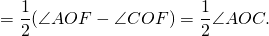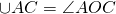Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
Видео:Геометрия 8 класс (Урок№27 - Теорема о вписанном угле.)Скачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Геометрия. Теорема о вписанном углеСкачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами | ||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||
Формула:  | ||||||||||||||||||||||||||||||||||||||
| Угол, образованный секущими секущими , которые пересекаются вне круга | ||||||||||||||||||||||||||||||||||||||
Формула:  | ||||||||||||||||||||||||||||||||||||||
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами | ||||||||||||||||||||||||||||||||||||||
| Угол, образованный касательной и хордой хордой , проходящей через точку касания | ||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||
Формула:  | ||||||||||||||||||||||||||||||||||||||
| Угол, образованный касательной и секущей касательной и секущей | ||||||||||||||||||||||||||||||||||||||
Формула:  | ||||||||||||||||||||||||||||||||||||||
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами | ||||||||||||||||||||||||||||||||||||||
| Угол, образованный двумя касательными касательными к окружности | ||||||||||||||||||||||||||||||||||||||
Формулы:  | ||||||||||||||||||||||||||||||||||||||
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:73. Теорема о вписанном углеСкачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:70 Теорема о вписанном углеСкачать  Вписанный угол окружностиВписанный угол окружности — это угол, образованный двумя хордами, исходящими из одной точки, то есть вписанным углом называется угол, вершина которого лежит на окружности. Угол ABC — вписанный угол. ∠ABC опирается на дугу AC, заключённую между его сторонами. Видео:Теорема о вписанном угле | Геометрия 7-9 класс #71 | ИнфоурокСкачать  Теорема о вписанном углеТеорема: Вписанный угол измеряется половиной дуги, на которую он опирается. Это следует понимать так: вписанный угол содержит в два раза меньше градусов, чем дуга, на которую он опирается:
При доказательстве этой теоремы следует рассмотреть три возможных случая расположения вписанного угла относительно центра окружности. Первый случай. Сторона вписанного угла проходит через центр окружности. Соединим точку A с центром круга (точкой O). Получим равнобедренный треугольник AOB, в котором AO = OB, как радиусы одной окружности. Следовательно, ∠A = ∠B, как углы при основании равнобедренного треугольника. Так как ∠AOC — внешний угол равнобедренного треугольника, то: а так как углы A и B равны, то
Но ∠AOC — центральный угол, значит ∠AOC =
Второй случай. Центр окружности лежит между сторонами вписанного угла. Проведём диаметр BD. Угол ABC разбился на два угла: ∠1 и ∠2. Точка D разделяет дугу AC на две дуги:
Следовательно, весь угол ABC будет измеряться половиной дуги AC:
Третий случай. Центр окружности лежит вне вписанного угла. Проведём диаметр BD. Но ∠ABD измеряется половиной дуги AD , а ∠CBD измеряется половиной дуги CD. Следовательно,
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Следствия из теоремы1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги. 2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности. Половина окружности содержит 180°, значит, угол, опирающийся на диаметр, содержит 90°. Видео:Углы, вписанные в окружность. 9 класс.Скачать  Чему равен вписанный уголВыясним, чему равен вписанный угол окружности и как его величина связана с величиной центрального угла. (О вписанном угле) Вписанный угол равен половине соответствующего ему центрального угла. 1) Рассмотрим частный случай, когда одна из сторон угла проходит через центр окружности.
∠AOC — внешний угол треугольника AOB. Внешний угол равен сумме двух внутренних углов, не смежных с ним: 2) Если центр окружности лежит между сторонами угла.
Аналогично, ∠AOF — внешний угол при вершине O равнобедренного треугольника ABO и ∠FOC — внешний угол при вершине O равнобедренного треугольника BCO и 3) Если центр окружности лежит вне угла.
∠AOF — внешний угол при вершине O равнобедренного треугольника ABO и ∠СOF — внешний угол при вершине O равнобедренного треугольника BCO и Что и требовалось доказать. Дугу окружности можно измерять в градусах. Если центральный угол AOC меньше либо равен 180º, то градусная мера дуги AC равна градусной мере центрального угла AOC: Если центральный угол AOC больше 180º, то градусная мера дуги AC равна 360º-∠AOC. Таким образом, сумма градусных мер двух дуг окружности с общими концами равна 360º. Другая формулировка теоремы о вписанном угле: Вписанный угол измеряется половиной дуги, на которую он опирается. 🎬 ВидеоУрок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать  Всё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать  Теорема о вписанном углеСкачать  Теорема о вписанном углеСкачать  Теорема о вписанном углеСкачать  Теорема о вписанном углеСкачать  Теорема о вписанных и центральных углахСкачать  ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать  Вписанный угол равен половине центрального углаСкачать 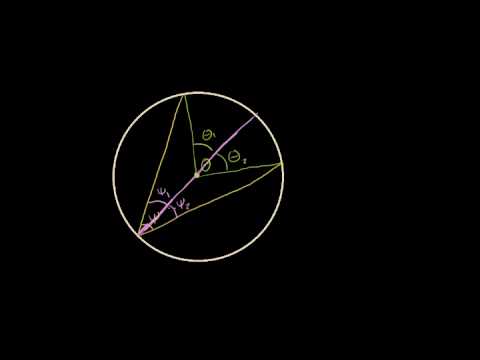 Вписанные и центральные углыСкачать  Окружность вписанная в треугольник и описанная около треугольника.Скачать  ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать  |





































 AC.
AC.






 Дано : окружность (O; R),
Дано : окружность (O; R),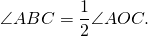
 В треугольнике AOB OA=OB (как радиусы). Значит, треугольник AOB — равнобедренный с основанием AB. Следовательно, у него углы при основании равны:∠ABO=∠BAO.
В треугольнике AOB OA=OB (как радиусы). Значит, треугольник AOB — равнобедренный с основанием AB. Следовательно, у него углы при основании равны:∠ABO=∠BAO. Проведем из вершины вписанного угла ABC диаметр BF.
Проведем из вершины вписанного угла ABC диаметр BF.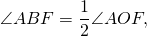
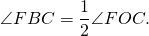
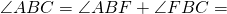
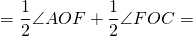
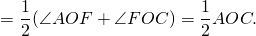
 Проведем диаметр BF.
Проведем диаметр BF.