Условимся обозначать символом положительно ориентированный угол, на который надо повернуть вектор , чтобы он стал сонаправлен с вектором. Если и, то точкам Р и Q соответствуют комплексные числа b-а и d-c (рис.7) и:
Эта формула в применении к положительно ориентированному треугольнику АВС дает:
Если z=r( ,то Отсюда:
Выведем формулу для площади S положительно ориентированного треугольника АВС:
что можно записать в виде определителя третьего порядка:
Если треугольник АВС вписан в окружность , то формула (29) преобразуется к виду:
Для площади S положительно ориентированного четырехугольника ABCD имеем:
Если четырехугольник ABCD вписан в окружность zz=l, то (32) принимает вид:
Три произвольно взятые точки всегда принадлежат либо одной окружности, либо одной прямой. Критерии принадлежности трех точек одной прямой рассмотрены выше.
Докажем КРИТЕРИЙ принадлежности четырех точек одной окружности или прямой.
Возьмем четыре произвольные точки A, В, С, D соответственно с комплексными координатами а, b,c,d. Комплексное число:
называется двойным отношением точек A, В, С, D и обозначается (AB, CD). Порядок точек существен.
Теорема. Для того чтобы, четыре точки лежали на одной прямой или на одной окружности, необходимо и достаточно, чтобы их двойное отношение было действительным числом.
Доказательство. Если точки А, В, С, D коллинеарны, то отношения и действительные числа (см. условие (10)). Следовательно, в этом случае будет действительным и двойное отношение (34). Если точки А, В, С, D лежат на окружности, то рассмотрим два возможных случая:
точки С и D находятся в одной полуплоскости от прямой АВ;
точки С и D находятся в различных полуплоскостях от прямой АВ.
В первом случае ориентированные углы ВСА и BDA равны, во втором случае ВСА+АDВ= ±, т. е. ВСА-ВСА= ±. В обоих случаях разность равна нулю или ±. Но поскольку согласно (24) эта разность равна:
то — действительное число.
Обратно: если двойное отношение четырех точек действительно, то эти точки или коллинеарны, или принадлежат одной окружности. В самом деле, тогда если действительное число, то и действительное число. Поэтому точки А, В, С коллинеарны и точки А, В, D коллинеарны, и, значит, все четыре точки коллинеарны. Если же число комплексное, то и число также комплексное, отличное от действительного. Поэтому точки A, B, С неколлинеарны и точки А, В, D также неколлинеарны. Так как по условию двойное отношение вещественно, то:
Следовательно, либо BCA=BDA, либо ВСА— ВDА=±, т.е. ВСА+ADB=±. В первом случае отрезок АВ из точек С и D виден под равными углами, и, стало быть, они принадлежат одной дуге окружности, стягиваемой хордой АВ. Во втором случае сумма противоположных углов четырехугольника ACBD равна ±, и поэтому он будет вписанным в окружность. Доказательство закончено.
Задача 1. В окружности проведены три параллельные хорды Доказать, что для произвольной точки М окружности прямые образуют равные углы соответственно с прямыми ВС, СА, АВ.
Решение. Принимая окружность за единичную, отнесем точкам А, В, С, A1, B1, C1 комплексные числа Тогда по условию (9) параллельности хорд имеем Следует доказать, что (рис.8).
Первое равенство эквивалентно такому:
т.е. эта дробь должна быть числом действительным. А это имеет место, поскольку сопряженное ей число:
равно этой же дроби. Аналогично доказывается и второе равенство углов.
Задача 2. На плоскости даны четыре окружности так, что окружности и пересекаются в точках и ; окружности и пересекаются в точках и , окружности и — в точках и и окружности и — в точках и . Доказать, что если точки лежат на одной окружности или прямой, то и точки также лежат на одной окружности или прямой (рис.9).
Решение. Согласно теореме этого параграфа и условию задачи будут действительными двойные отношения:
Поэтому будет действительным и число:
Следовательно, из вещественности двойного отношения вытекает вещественность и двойного отношения .
- Признак принадлежности четырёх точек одной окружности
- Четыре точки на окружности теорема
- Признак принадлежности четырёх точек одной окружности
- Углы и площади. Критерий принадлежности четырех точек одной окружности
- ПРИНАДЛЕЖНОСТЬ ЧЕТЫРЕХ ТОЧЕК ОКРУЖНОСТИ В ОЛИМПИАДНЫХ ЗАДАЧАХ ПО ГЕОМЕТРИИ Текст научной статьи по специальности « Математика»
- Аннотация научной статьи по математике, автор научной работы — Морщинкина Юлия Дмитриевна, Сорокина Марина Валерьевна
- Похожие темы научных работ по математике , автор научной работы — Морщинкина Юлия Дмитриевна, Сорокина Марина Валерьевна
- Текст научной работы на тему «ПРИНАДЛЕЖНОСТЬ ЧЕТЫРЕХ ТОЧЕК ОКРУЖНОСТИ В ОЛИМПИАДНЫХ ЗАДАЧАХ ПО ГЕОМЕТРИИ»
- 📺 Видео
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Признак принадлежности четырёх точек одной окружности
Признак принадлежности четырёх точек одной окружности
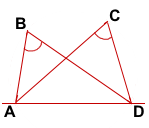
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.
Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,
Доказать: точки A, B, C, D лежат на одной окружности
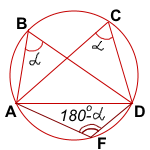
Опишем около треугольника ABD окружность.
Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.
Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:
Рассмотрим четырехугольник ACDF.
Отсюда следует, что четырёхугольник ABDF — вписанный.
Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.
Видео:Условие принадлежности четырёх точек одной окружностиСкачать

Четыре точки на окружности теорема
Видео:Первое условие принадлежности четырех точек одной окружностиСкачать

Признак принадлежности четырёх точек одной окружности
Признак принадлежности четырёх точек одной окружности
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.
Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,
Доказать: точки A, B, C, D лежат на одной окружности

Опишем около треугольника ABD окружность.
Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.
Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:
Рассмотрим четырехугольник ACDF.
Отсюда следует, что четырёхугольник ABDF — вписанный.
Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Углы и площади. Критерий принадлежности четырех точек одной окружности
Условимся обозначать символом положительно ориентированный угол, на который надо повернуть вектор , чтобы он стал сонаправлен с вектором. Если и, то точкам Р и Q соответствуют комплексные числа b-а и d-c (рис.7) и:
Эта формула в применении к положительно ориентированному треугольнику АВС дает:
Если z=r( ,то Отсюда:
Выведем формулу для площади S положительно ориентированного треугольника АВС:
что можно записать в виде определителя третьего порядка:
Если треугольник АВС вписан в окружность , то формула (29) преобразуется к виду:
Для площади S положительно ориентированного четырехугольника ABCD имеем:
Если четырехугольник ABCD вписан в окружность zz=l, то (32) принимает вид:
Три произвольно взятые точки всегда принадлежат либо одной окружности, либо одной прямой. Критерии принадлежности трех точек одной прямой рассмотрены выше.
Докажем КРИТЕРИЙ принадлежности четырех точек одной окружности или прямой.
Возьмем четыре произвольные точки A, В, С, D соответственно с комплексными координатами а, b,c,d. Комплексное число:
называется двойным отношением точек A, В, С, D и обозначается (AB, CD). Порядок точек существен.
Теорема. Для того чтобы, четыре точки лежали на одной прямой или на одной окружности, необходимо и достаточно, чтобы их двойное отношение было действительным числом.
Доказательство. Если точки А, В, С, D коллинеарны, то отношения и действительные числа (см. условие (10)). Следовательно, в этом случае будет действительным и двойное отношение (34). Если точки А, В, С, D лежат на окружности, то рассмотрим два возможных случая:
точки С и D находятся в одной полуплоскости от прямой АВ;
точки С и D находятся в различных полуплоскостях от прямой АВ.
В первом случае ориентированные углы ВСА и BDA равны, во втором случае ВСА+АDВ= ±, т. е. ВСА-ВСА= ±. В обоих случаях разность равна нулю или ±. Но поскольку согласно (24) эта разность равна:
то — действительное число.
Обратно: если двойное отношение четырех точек действительно, то эти точки или коллинеарны, или принадлежат одной окружности. В самом деле, тогда если действительное число, то и действительное число. Поэтому точки А, В, С коллинеарны и точки А, В, D коллинеарны, и, значит, все четыре точки коллинеарны. Если же число комплексное, то и число также комплексное, отличное от действительного. Поэтому точки A, B, С неколлинеарны и точки А, В, D также неколлинеарны. Так как по условию двойное отношение вещественно, то:
Следовательно, либо BCA=BDA, либо ВСА— ВDА=±, т.е. ВСА+ADB=±. В первом случае отрезок АВ из точек С и D виден под равными углами, и, стало быть, они принадлежат одной дуге окружности, стягиваемой хордой АВ. Во втором случае сумма противоположных углов четырехугольника ACBD равна ±, и поэтому он будет вписанным в окружность. Доказательство закончено.
Задача 1. В окружности проведены три параллельные хорды Доказать, что для произвольной точки М окружности прямые образуют равные углы соответственно с прямыми ВС, СА, АВ.
Решение. Принимая окружность за единичную, отнесем точкам А, В, С, A1, B1, C1 комплексные числа Тогда по условию (9) параллельности хорд имеем Следует доказать, что (рис.8).
Первое равенство эквивалентно такому:
т.е. эта дробь должна быть числом действительным. А это имеет место, поскольку сопряженное ей число:
равно этой же дроби. Аналогично доказывается и второе равенство углов.
Задача 2. На плоскости даны четыре окружности так, что окружности и пересекаются в точках и ; окружности и пересекаются в точках и , окружности и — в точках и и окружности и — в точках и . Доказать, что если точки лежат на одной окружности или прямой, то и точки также лежат на одной окружности или прямой (рис.9).
Решение. Согласно теореме этого параграфа и условию задачи будут действительными двойные отношения:
Поэтому будет действительным и число:
Следовательно, из вещественности двойного отношения вытекает вещественность и двойного отношения .
Видео:ОКРУЖНОСТЬ (признак принадлежности четырех точек одной окружности) ЧАСТЬ 4Скачать

ПРИНАДЛЕЖНОСТЬ ЧЕТЫРЕХ ТОЧЕК ОКРУЖНОСТИ В ОЛИМПИАДНЫХ ЗАДАЧАХ ПО ГЕОМЕТРИИ Текст научной статьи по специальности « Математика»
Видео:Принадлежность четырех точек одной окружности. Попытка 2.Скачать

Аннотация научной статьи по математике, автор научной работы — Морщинкина Юлия Дмитриевна, Сорокина Марина Валерьевна
Рассматривается вопрос необходимости и достаточности условий принадлежности четырех точек окружности . Приведены примеры заданий олимпиадного характера, в которых применяются различные критерии, такие как равноудаленность точек от центра, критерий вписанного четырехугольника , теорема, обратная равенству углов, опирающихся на одну хорду , свойства хорд , секущих и др.
Видео:Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

Похожие темы научных работ по математике , автор научной работы — Морщинкина Юлия Дмитриевна, Сорокина Марина Валерьевна
Видео:ЕГЭ Задание 16 Условие принадлежности четырех точек окружностиСкачать

Текст научной работы на тему «ПРИНАДЛЕЖНОСТЬ ЧЕТЫРЕХ ТОЧЕК ОКРУЖНОСТИ В ОЛИМПИАДНЫХ ЗАДАЧАХ ПО ГЕОМЕТРИИ»
ПРИНАДЛЕЖНОСТЬ ЧЕТЫРЕХ ТОЧЕК ОКРУЖНОСТИ В ОЛИМПИАДНЫХ ЗАДАЧАХ ПО ГЕОМЕТРИИ
Ю. Д. Морщинкина1, М. В. Сорокина2
1’2Пензенский государственный университет, Пенза, Россия
1 juliamorwinkina@mail.ru 2 sorokina_m@list.ru
Аннотация. Рассматривается вопрос необходимости и достаточности условий принадлежности четырех точек окружности. Приведены примеры заданий олимпиадного характера, в которых применяются различные критерии, такие как равноудаленность точек от центра, критерий вписанного четырехугольника, теорема, обратная равенству углов, опирающихся на одну хорду, свойства хорд, секущих и др.
Ключевые слова: олимпиадная задача по геометрии, окружность, вписанный угол, вписанный четырехугольник, хорда, секущая
Для цитирования: Морщинкина Ю. Д., Сорокина М. В. Принадлежность четырех точек окружности в олимпиадных задачах по геометрии // Вестник Пензенского государственного университета. 2021. № 4. С. 55-62.
В последние годы в образовательном процессе уделяется все больше внимания работе с одаренными детьми. Олимпиады различного уровня прочно вошли в школьную жизнь, и предметная подготовка обучающихся должна постоянно совершенствоваться. Дети, имеющие способности и интерес к предмету, с большим желанием включаются в работу олимпиадного движения. Однако, в такой предметной области, как математика, продвижение по пути решения нестандартных задач сопряжено с огромной работой. В учебном процессе учителем должна быть продумана система подготовки таких детей, разработаны программы, формирующие целостную систему математического знания, а также некоторые универсальные приемы работы с нестандартными задачами. Олим-пиадные задачи по геометрии характеризуются, конечно, нестандартностью подхода к решению. Это проявляется в нескольких аспектах: умение переформулировать требование задачи; умение грамотно выполнить чертеж, умение анализировать задачную ситуацию и искать путь решения и др. Олимпиадная задача по геометрии — это, как правило, задача на доказательство. Поэтому необходимо умение строить логическую цепочку умозаключений. Многие участники олимпиад, успешно справляющиеся с заданиями логического и алгебраического характера, испытывают трудности при решении задач по геометрии. В работе мы хотим остановиться на вопросе решения задачи на доказательство принадлежности четырех (или более) точек окружности. Задания подобного рода часто встречаются и во Всероссийской олимпиаде школьников по математике, и в уров-невых олимпиадах.
В школьном курсе геометрии окружность изучается достаточно подробно: дается определение, рассматриваются свойства углов, вписанных в окружность, теоремы, относящиеся к свойствам касательных, секущих, хорд [1]. Доказываются теоремы о треугольниках и четырехугольниках, вписанных в окружность. Поэтому в большинстве своем
© Морщинкина Ю. Д., Сорокина М. В., 2021
задачи, касающиеся принадлежности четырех точек окружности, у учащихся ассоциируются с четырехугольником, вписанным в окружность. При подготовке к олимпиадам необходимо рассмотреть вопрос равносильных преобразований этого требования, чтобы обучающиеся могли свободно оперировать фактами, выбирая тот, который будет наиболее удобным в каждом конкретном случае. Рассмотрим некоторые возможные варианты доказательства принадлежности четырех точек окружности.
1. Равноудаленность четырех точек от некоторой точки плоскости.
Это требование непосредственно вытекает из определения окружности, как геометрического места точек, равноудаленных от данной. И если в задаче возможно отыскание точки, равноудаленной от трех данных точек, то доказательство может быть проведено на основе именно равноудаленности, т.е. нужно рассматривать равенство четырех отрезков (радиусов окружности). Приведем пример задания, решение которого можно рассматривать с учащимися 8-9 классов.
Задача 1. На плоскости даны две пересекающиеся окружности. Точка А — одна из двух точек пересечения. В каждой окружности проведен диаметр, параллельный касательной в точке А к другой окружности, причем эти диаметры не пересекаются (рис. 1). Докажите, что концы этих диаметров лежат на одной окружности [2, № 108640].
Обозначим ш1 — окружность с центром в точке О и Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
HC AH HA CH AS CT
Из (9) и (10) следует: -=-. Значит, прямые АС и ST параллельны.
Четырехугольник HSKT — параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам. Если ST о HK = D, то D — середина отрезка ST, HD — медиана треугольника HST.
Так ST\AC, то лАНС -aSHT, следовательно, прямая НК, пересекающая сторону ST в ее середине, проходит через середину стороны АС. Значит, прямая HK содержит точку M.
Мы показали, что точка K, лежащая на окружности ю, принадлежит биссектрисе угла B и отрезку HM, следовательно, она совпадает с точкой R, поэтому R ею, что и требовалось доказать.
Мы рассмотрели несколько способов доказательства принадлежности точек окружности. Следует отметить, что существуют и другие варианты, например, использование симметрий или доказательство того, что четыре точки образуют четырехугольник специального вида. Примеры приведенных заданий позволят развить геометрический кругозор учащихся и будут полезны при подготовке к олимпиадам.
1. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. [и др.]. Геометрия. 7-9 классы : учеб. для обще-образоват. организаций. 3-е изд. М. : Просвещение , 2015. 383 с.
2. Интернет-проект «Задачи». URL: http:// www.problems.ru. (дата обращения: 02.04.2021).
Информация об авторах Морщинкина Юлия Дмитриевна, студентка, Пензенский государственный университет.
Сорокина Марина Валерьевна, кандидат физико-математических наук, доцент, доцент кафедры «Математическое образование», Пензенский государственный университет.
Авторы заявляют об отсутствии конфликта интересов.
📺 Видео
ОГЭ Задание 25 Условие принадлежности четырёх точек одной окружностиСкачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Первое условие принадлежности четырех точек окружностиСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

16 задание. Профильный ЕГЭ 2023. 9 точек окружности, окружность Эйлера. Что это?Скачать

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Доказать, что точки лежат на одной окружностиСкачать

Окружность. 7 класс.Скачать

Теорема о числе точек пересечения двух окружностейСкачать

Математика это не ИсламСкачать

10 класс, 11 урок, Числовая окружностьСкачать