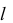Тело вращения поверхность вращения получаемая вращением образующей окружности вокруг оси (2 видео)

Тела вращения

Тела вращения — это объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости. Шар — образован полукругом, вращающимся вокруг диаметра разреза.

Содержание:

Содержание

Понятие о поверхностях и телах вращения
Цилиндр
Призма, вписанная в цилиндр и описанная около него
Пример:
Конус
Пример:
Пирамида, вписанная в конус и описанная около него
Пример:
Части шара и сферы
Конспекты по математике на тему «Тела вращения. Объемы тел вращения»
Поверхности вращения в начертательной геометрии с примерами
Поверхности вращения
Пересечение поверхностей вращения плоскостью
Развертки поверхностей вращения
Приближенные развертки
Условные развертки
🌟 Видео

Понятие о поверхностях и телах вращения

Если многоугольник ABCDE вращается вокруг прямой АВ (рис. 2.257), то каждая его точка, не принадлежащая прямой АВ, описывает окружность с центром на этой прямой. Весь многоугольник ABCDE при этом описывает некоторое тело вращения (рис. 2.258); прямая АВ — ось этого тела.

Плоскость, проходящая через ось тела вращения, является его плоскостью симметрии. Таких плоскостей каждое тело вращения имеет бесконечно много.

Любая плоскость, проходящая через ось тела вращения, пересекает это тело. Полученное сечение называют осевым сечением. В частности, осевое сечение тела вращения может состоять из двух изолированных друг от друга плоских фигур, симметричных относительно оси (рис. 2.259). Все осевые сечения тела вращения равны.

Чтобы задать тело вращения, достаточно указать его ось и фигуру, вращением которой получено данное тело. Описывая такое тело словесно, вместо оси иногда указывают принадлежащий ей отрезок. Например, вместо «тело, образованное вращением треугольника вокруг оси, содержащей его сторону» говорят и короче: «тело, образованное вращением треугольника вокруг его стороны».

Цилиндр

Можно дать определение цилиндра.

Определение. Цилиндром (точнее, круговым цилиндром) называют тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называют основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов — образующими цилиндра (рис. 2.260, 2.261).

Можно доказать, что основания цилиндра равны и лежат в параллельных плоскостях, что у цилиндра образующие параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.

Определение. Цилиндр называют прямым, если его образующие перпендикулярны плоскостям оснований.

На рисунке 2.261 изображен наклонный цилиндр, а на рис. 2.260 — прямой. В школьном курсе, как правило, рассматривают только прямые цилиндры, называя их для краткости просто цилиндрами.

Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг одной из его сторон как оси (рис. 2.262).

Радиусом цилиндра называют радиус его основания. Высотой цилиндра называют расстояние между плоскостями оснований. Осью цилиндра называют прямую, проходящую через центры оснований. Ось цилиндра параллельна образующим.

Сечение цилиндра плоскостью, проходящей через ось цилиндра, называют осевым сечением цилиндра (рис. 2.263). Именно через такое сечение обозначают цилиндр. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра (рис. 2.264).

Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

На рисунке 2.265 изображено сечение цилиндра плоскостью, параллельной его оси. Оно представляет собой прямоугольник.

Если цилиндр с радиусом основания разрезать по образующей (рис. 2.266) и развернуть на плоскости, получится прямоугольник, стороны которого — спрямленная окружность основания и образующая — развертка боковой поверхности цилиндра. Чтобы получить развертку полной поверхности, надо присоединить два круга — основания цилиндра (рис. 2.267).

Призма, вписанная в цилиндр и описанная около него

При решении геометрических задач часто приходится рассматривать комбинации многогранников и цилиндров, в частности, призм, вписанных в цилиндр и описанных около цилиндра.

Определение. Призмой, вписанной в цилиндр, называют такую призму, основания которой — равные многоугольники, вписанные в основания цилиндра. Ее боковые ребра являются образующими цилиндра (рис. 2.268).

Определение. Призму называют описанной около цилиндра, если ее основания — равные многоугольники, описанные около основания цилиндра. Плоскости ее граней касаются боковой поверхности цилиндра (рис. 2.269).

Пример:

В цилиндр вписана правильная шестиугольная призма. Найдите угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.

Решение:

Из условия задачи имеем (рис. 2.270):

1. В цилиндр вписана правильная шестиугольная призма.

2. Радиус основания цилиндра равен высоте призмы

3. Требуется найти угол между

4. (1, свойства правильного шестиугольника, вписанного в окружность).

5. — квадрат (1, 4, определение квадрата).

Надо найти угол между Как это сделать? Лучше всего рассмотреть осевое сечение призмы, изображенное на рисунке 2.271. Задача сводится к нахождению угла .

6. = 45° (найдите самостоятельно).

Конус

Определение. Конусом (точнее, круговым конусом) называют тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга, — вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называют образующими конуса (рис. 2.272).

Поверхность конуса состоит из основания и боковой поверхности.

Определение. Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (рис. 2.272).

На рисунке 2.273 изображен наклонный конус, в дальнейшем будет рассматриваться только прямой конус, называемый для краткости просто конусом.

Прямой круговой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси (рис. 2.274).

Определение. Высотой конуса называют перпендикуляр, опущенный из его вершины на плоскость основания.

У прямого конуса основание высоты совпадает с центром основания (рис. 2.272). Осью прямого конуса называется прямая, содержащая его высоту. У наклонного конуса основание высоты может не совпадать с центром круга, лежащего в основания конуса (рис. 2.273).

Если конус РАВ с радиусом основания и образующей (рис. 2.275) разрезать по образующей РВ и развернуть на плоскости, то получим развертку.

Развертка конуса будет состоять из сектора ВРАВ и круга (основания) диаметра

Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса (рис. 2.276).

Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность — по окружности с центром на оси конуса.

Плоскость, перпендикулярная оси конуса, отсекает от него меньший конус. Оставшуюся часть называют усеченным конусом (рис. 2.277).

Усеченный конус можно получить и как тело вращения.

Определение. Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям.

Круги О и — его основания (рис. 2.277), его образующие равны между собой, прямая — ось, отрезок — высота. Его осевое сечение — равнобедренная трапеция.

Пример:

Конус пересечен плоскостью, параллельной основанию, на расстоянии d от вершины. Найдите площадь сечения, если радиус основания конуса R, а высота Н.

Решение:

Из условия задачи имеем:

1. Конус с вершиной S.

4. OA = R. (рис. 2.278)

5. Плоскость пересекает конус и параллельна основанию.

6. Найдите площадь сечения конуса.

7. Сечение конуса получается из основания конуса преобразованием гомотетии относительно вершины конуса с коэффициентом гомотетии (1, 2, 3, 4, 5, определение гомотетии).

8. Радиус круга в сечении (7).

9. Площадь сечения (8, теорема о площади круга).

Пирамида, вписанная в конус и описанная около него

Определение. Пирамидой, вписанной в конус, называют такую пирамиду, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса. Боковые ребра пирамиды, вписанной в конус, являются образующими конуса (рис. 2.279).

Определение. Пирамиду называют описанной около конуса, а конус — вписанным в пирамиду, если ее основанием является многоугольник, описанной около основания конуса, а вершина совпадает с вершиной конуса. Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса (рис. 2.280).

Определение. Шаром называют тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Эту точку называют центром шара, а данное расстояние — радиусом шара (рис. 2.281).

Границу шара называют шаровой поверхностью или сферой. На рисунке 2.281 точки А, В и D принадлежат сфере, а, например, точка М ей не принадлежит. Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называют радиусом.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называют диаметром. Концы любого диаметра называют диаметрально противоположными точками шара.

Шар так же, как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра, как оси (рис. 2.282).

Теорема 62. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Если шар с центром О и радиусом R пересечен плоскостью , то в сечении по теореме 62 получается круг радиуса с центром К (рис. 2.283).

Радиус сечения шара плоскостью можно вычислить по формуле

Из формулы видно, что плоскости, равноудаленные от центра, пересекают шар по равным кругам. Радиус сечения шара тем больше, чем ближе секущая плоскость к центру шара, т. е. чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.

Плоскость, проходящую через центр шара, называют диаметральной плоскостью. Сечение шара диаметральной плоскостью называют большим кругом, а сечение сферы — большой окружностью.

Теорема 63. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

Плоскость, проходящую через точку А шаровой поверхности и перпендикулярную радиусу, проведенному в точку А, называют касательной плоскостью. Точку А называют точкой касания (рис. 2.284).

Теорема 64. Касательная плоскость имеет с шаром только одну общую точку — точку касания.

Прямую, проходящую через точку А шаровой поверхности перпендикулярно к радиусу, проведенному в эту точку, называют касательной (рис. 2.285).

Теорема 65. Через любую точку шаровой поверхности проходит бесконечно много касательных, причем все они лежат в касательной плоскости шара.

Пример:

Через середину радиуса шара проведена перпендикулярная радиусу плоскость. Как относится площадь полученного сечения к площади большого круга?

Решение:

Из условия задачи имеем:

1. Шар с центром О и радиусом R, ОС = OA = R.

2. ОВ = ВС = .

3. СО перпендикулярен плоскости окружности с центром в точке В.

4. Найдите отношение площади круга с центром в точке В к площади большого круга.

Чтобы решить задачу, надо знать радиус получающегося в сечении круга с центром в точке В. Как его найти?

5. — прямоугольный (3, определение перпендикуляра к плоскости).

6. Если радиус шара R, то радиус круга в сечении будет

7. Отношение площади этого круга к площади большого круга равно (1, 2, 5, теорема Пифагора).

Части шара и сферы

В геометрии существуют специальные названия частей сферы и шара, которые получаются при разбиении этих фигур на части отрезками, прямыми или плоскостями.

Определение. Часть шара, отсекаемую плоскостью, называют шаровым сегментом.

Шаровой сегмент ограничен: 1) частью сферы, которую называют сегментной поверхностью; 2) кругом, который называют основанием шарового сегмента.

На рис. 2.287 плоскость , проходящая через точку В, отсекает от шара два шаровых сегмента.

Определение. Сферическим сегментом называют часть сферы, отсекаемую плоскостью.

Окружность, по которой плоскость пересекает сферу, называют основанием сферического сегмента.

Высотой шарового сегмента и сегментной поверхности называют отрезок радиуса, перпендикулярного к основанию сегмента. На рисунке 2.287 верхний сегмент имеет высоту АВ.

Если пересечь шар двумя параллельными плоскостями, тогда шар (его граничная сфера) разделится на три части, две из них — шаровые (сферические) сегменты.

Определение. Часть шара, заключенную между двумя пересекающими его параллельными плоскостями, называют шаровым слоем.

На рисунке 2.288 две параллельные плоскости, проходящие через точки СВ, отсекают от шара шаровой слой.

Определение. Сферическим поясом называют часть сферы, заключенную между двумя ее параллельными сечениями.

Поверхность шарового слоя состоит из двух кругов, называемых основаниями шарового слоя, и сферического пояса соответственно.

Высотой шарового слоя называют перпендикуляр, проведенный из точки одного основания к плоскости другого; чаще всего берут за высоту отрезок диаметра сферы, перпендикулярного основаниям, с концами на них. Высотой сферического пояса называют высоту соответствующего шарового слоя. На рисунке 2.288 высотой шарового слоя является отрезок ВС.

Сферический сегмент и сферический пояс можно рассматривать как поверхности, образованные вращением некоторых дуг окружности вокруг прямой АВ (рис. 2.288).

Шаровой сектор — это часть шара, получаемая не простым сечением шара плоскостью (или плоскостями), а как фигура, образованная при вращении соответствующего кругового сектора (рис. 2.289).

Определение. Шаровым сектором называют фигуру, полученную при вращении кругового сектора с углом, меньшим 90°, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.

Шаровой сектор состоит из шарового сегмента и конуса. На рисунке 2.290 изображен круговой сектор СО А (О — центр данного круга). Вращая круговой сектор СО А вокруг радиуса АО, получим шаровой сектор с центром в точке О (рис. 2.290). Полученный шаровой сектор состоит из шарового сегмента высотой Н и конуса с вершиной в точке О и высотой R — Н.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Видео:1.3 ПОВЕРХНОСТИ ВРАЩЕНИЯСкачать

Конспекты по математике на тему «Тела вращения. Объемы тел вращения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Конспекты занятий по математике для студентов первого курса теме «Тела вращения. Объемы тел вращения».

Тела вращения — объёмные тела, полученные при вращении плоской фигуры вокруг своей оси или стороны.

Примеры тел вращения: цилиндр, конус, шар, сфера.

Цили́ндр (от греч. kýlindros, валик, каток) — геометрическое тело, образованное вращением прямоугольника вокруг одной из сторон.

Цилиндр состоит из двух параллельных кругов, не лежащих в одной плоскости, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, — образующими цилиндра.

Примеры тел, имеющих цилиндрическую форму: часть водопроводной трубы, консервная банка.

Радиусом цилиндра называется радиус его основания.

Высотой цилиндра называется расстояние между его основаниями.

Осью цилиндра называется прямая, проходящая через центр оснований, параллельно образующим.

Осевое сечение – сечение цилиндра плоскостью, проходящей через его ось.

Поверхность цилиндра состоит из оснований и боковой поверхности.

Боковая поверхность составлена из образующих.

Цилиндр называется прямым , если его образующие перпендикулярны плоскостям оснований.

Основания цилиндра равны и параллельны.

Образующие цилиндра равны и параллельны.

Ко́нус — тело вращения, образованное вращением прямоугольного треугольника, вокруг одного из его катетов.

Конус состоит из круга – основания конуса, вершины конуса — точки, не лежащей в плоскости основания, и всех отрезков, соединяющих вершину конуса с точками основания.

Примеры тел, имеющих форму конуса: воронка для наливания жидкости, чум — жилье народов севера, мороженое-рожок.

Отрезок, соединяющий вершину и границу основания, называется образующей конуса .

Боковая поверхность конуса — объединение образующих конуса.

Отрезок, опущенный перпендикулярно из вершины на плоскость основания, называется высотой конуса .

Конус называется прямым , если прямая ( ось конуса ), соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.

Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением .

Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом .

Шар — тело вращения, полученное вращением полукруга около его неподвижного диаметра.

Примеры тел, имеющих форму шара или сферы: мыльный пузырь, земля, футбольный и теннисный мячи.

Любой отрезок, соединяющий центр шара с точкой его поверхности, называется радиусом .

Сфера это поверхность шара .

Отрезок, соединяющий две точки шаровой поверхности и проходящей через центр шара, называется диаметром .

Концы любого диаметра называются диаметрально противоположными точками шара.

Диаметр называется осью шара , а его оба конца — полюсами шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью.

Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью . Точка А называется точкой касания .

Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом . Другие плоские сечения шара называются малыми кругами.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

1. Уравнение шара с радиусом R и центром в начале декартовой системе координат :

x 2 + y 2 + z 2 ≤ R 2

2. Уравнение шара с радиусом R и центром в точке с координатами (x ₀ , y ₀ , z ₀ ) в декартовой системе координат :

(x — x ₀ ) 2 + (y — y ₀ ) 2 + (z — z ₀ ) 2 ≤ R 2

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :

x 2 + y 2 + z 2 = R 2

2. Уравнение сферы с радиусом R и центром в точке с координатами (x ₀ , y ₀ , z ₀ ) в декартовой системе координат :

(x — x ₀ ) 2 + (y — y ₀ ) 2 + (z — z ₀ ) 2 = R 2

Формулы объема цилиндра, конуса и шара.

Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.

Объем прямого цилиндра равен произведению площади основания на высоту: V = S _осн h , т.к. в основании цилиндра лежит круг, то S _осн = S _круга =π R 2 . Тогда формула объема цилиндра примет вид: V = π R 2 h .

Конус — геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.

Объем конуса равен одной трети произведения площади основания на высоту V = S _осн h , т.к. в основании конуса лежит круг, то S _осн =S _круга =πR 2 . Тогда формула объема цилиндра примет вид: V = πR 2 h .

3. Объем усеченного конуса.

Усеченный конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.

Шар — это геометрическое тело, состоящее из точек пространства, которые удалены от центра O на одинаковое расстояние R .

Объем шара радиуса R равен V = π R 3 .

Видео:Геометрия 9 класс (Урок№34 - Тела и поверхности вращения.)Скачать

Поверхности вращения в начертательной геометрии с примерами

Содержание:

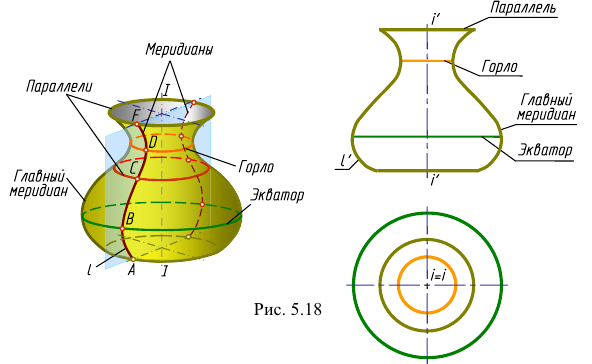
Поверхностей вращения существует множество: цилиндр, конус, сфера, эллипсоиды, торы и др. Поверхность вращения общего вида образуется вращательным перемещением образующей линии вокруг неподвижной оси. Каждая точка образующей линии при вращении вокруг неподвижной оси описывает окружность с центром на оси вращения. Эти окружности называются параллелями.

Наибольшую из параллелей (окружностей) поверхности вращения называют экватором поверхности, а наименьшую — горлом (шейкой) поверхности. Плоскости, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность, — меридианами. Меридиональная плоскость, параллельная плоскости проекции, называется плоскостью главного меридиана, а линия пересечения этой плоскости с поверхностью вращения называется главным меридианом.

Видео:Объем тела вращения на примере тора. 2 способаСкачать

Поверхности вращения

Поверхностью вращения называется поверхность, описываемая кривой (или прямой) образующей при ее вращении вокруг неподвижной оси (рис. 5.18). Эта поверхность определяется на чертеже заданием образующей и оси вращения.

Каждая точка образующей

Плоскость, проходящую через ось поверхности вращения, называют меридиональной. Линию ее пересечения с поверхностью — меридианом. Меридиан, параллельный фронтальной плоскости проекций, называется главным меридианом. Все меридианы равны между собой.

На чертеже ось вращения располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.

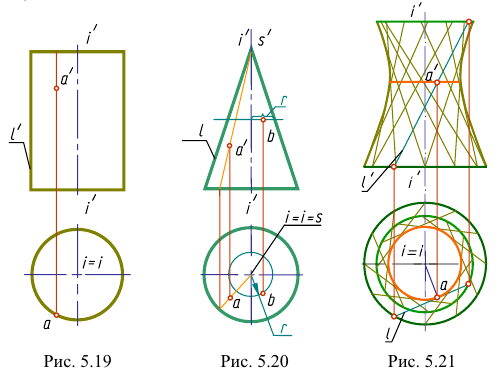
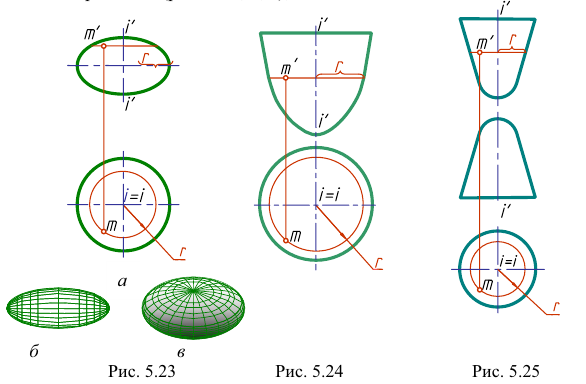
Точки на поверхностях вращения могут быть построены с помощью параллелей, то есть окружностей на поверхности (рис. 5.20, рис. 5.22, а, б, в, рис. 5.23 — рис. 5.25).

Рассмотрим некоторые тела и поверхности вращения.

1 .Поверхности, образованные вращением прямой линии:

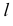
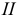
а) цилиндр вращения — поверхность, полученная вращением прямой вокруг параллельной ей оси (рис. 5.19);

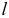
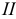
б) конус вращения — поверхность, образованная вращением прямой вокруг пересекающейся с ней осью (рис. 5.20);

в) однополостный гиперболоид вращения — поверхность, полученная вращением прямой вокруг скрещивающейся с ней осью (рис. 5.21).

Точка А, лежащая на перпендикуляре к оси вращения и образующей, будет описывать наименьшую окружность, являющуюся горлом гиперболоида. Однополостный гиперболоид может быть также получен вращением гиперболы вокруг ее мнимой оси.

2. Поверхности, образованные вращением окружности вокруг неподвижной оси: а) сфера — поверхность, полученная вращением окружности вокруг ее диаметра (рис. 5. 22, а);

б) тор — поверхность, полученная вращением окружности вокруг оси лежащей в плоскости этой окружности, но не проходящей через ее центр (рис. 5.22, б-д).

Если ось вращения проходит вне окружности, то поверхность называется «открытый тор» или «тор — кольцо» (рис. 5.22, б); если ось касается окружности, то образованная поверхность называются «закрытый тор» (рис. 5.22, в); если ось пересекает окружность — «самопересекающийся тор» (рис. 5.22, г, д)). Тор, изображенный на рис. 5.22, г, называется также «тор-яблоко», а на рис. 5.22, д — «тор-лимон». Сфера — частный случай торовой поверхности.

3. Поверхности вращения, образованные вращением кривых второго порядка:

а) эллипсоид вращения — поверхность, полученная вращением эллипса вокруг оси (рис. 5.23). Поверхность, образованная вращением эллипса вокруг его большой оси, называется вытянутым эллипсоидом вращения (рис. 5.23, б), при вращении вокруг малой оси — сжатым элипсоидом вращения (рис. 5.23, а, в);

б) параболоид вращения — поверхность, образованная вращением параболы вокруг ее оси (рис. 5.24);

в) двухполостный гиперболоид вращения — поверхность, образованная вращением гиперболы вокруг ее действительной оси (рис. 5.25).

Пересечение поверхностей вращения плоскостью

При пересечении поверхности вращения плоскостью получается линия сечения — плоская фигура. Построение проекций линии пересечения необходимо начинать с определения опорных точек. К ним относятся точки, расположенные на очерковых образующих поверхности (точки, определяющие границы видимости проекций кривой), и точки, удаленные на экстремальные (максимальное и минимальное) расстояния от плоскостей проекций. После этого определяют произвольные (промежуточные) точки линии пересечения.

Для определения точек, принадлежащих линии пересечения, можно использовать различные методы. Один из них — метод вспомогательных секущих плоскостей. Суть его заключается в том, что заданные плоскость и поверхность вращения пересекают вспомогательными плоскостями. Находят линии пересечения этой плоскости с заданными плоскостью и поверхностью вращения. Затем отмечают точки, в которых пересекаются полученные линии пересечения. Построенные точки фигуры сечения соединяют плавной кривой линией.

Развертки поверхностей вращения

Построение разверток поверхностей вращения имеет большое значение, особенно при конструировании из листового материала моделей различных сооружений, форм для металлических отливок, сосудов, трубопроводов, резервуаров и т.п.

Приближенные развертки

Поверхности, которые можно совместить с плоскостью без разрывов и складок, называют развертывающимися поверхностями. Фигуру, полученную при совмещении развертывающейся поверхности с плоскостью, называют разверткой. Для развертывающихся поверхностей можно построить приближенную развертку (условно-развертываемые поверхности). При построении приближенной развертки поверхность аппроксимируют поверхностями вписанных или описанных многогранников, имеющих грани в форме прямоугольников или треугольников. Поэтому при графическом выполнении разверток поверхности всегда приходится производить разгибание или спрямление кривых линий, принадлежащих поверхности, что неизбежно приводит к потере точности.

Условные развертки

Неразвертывающиеся поверхности не могут быть совмещены сплоскостью без разрывов и складок, т.е. теоретически они не имеют своей развертки. Поэтому говорят лишь об условном решении задачи по построению разверток неразвертывающихся поверхностей. На практике для получения развертки неразвертываемой поверхности, выполненной из листового материала, приходится кроме изгибания производить растяжение и сжатие определенных участков листа.

Построение условной развертки неразвертывающейся поверхности состоит в том, что отсеки заданной поверхности аппроксимируются отсеками развертывающихся поверхностей — гранными, цилиндрическими или коническими.

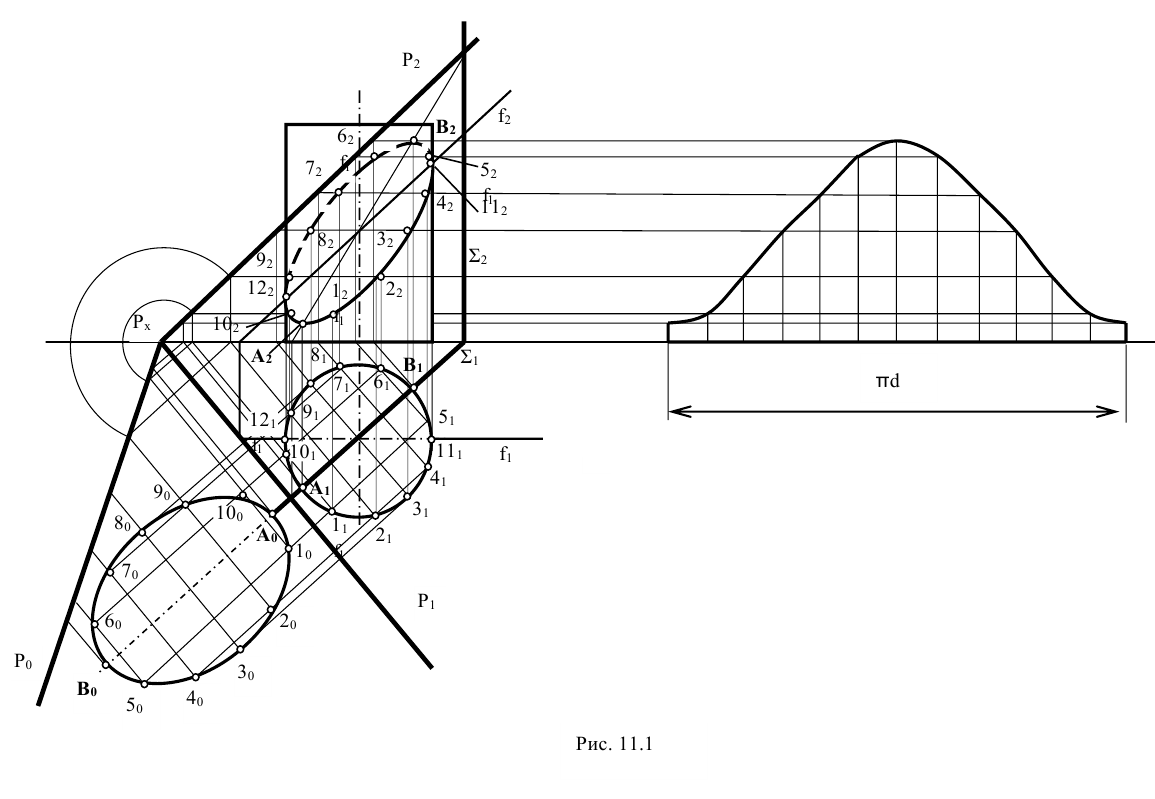
Задание: построить проекции и натуральный вид фигуры сечения поверхности цилиндра плоскостью Р (рис. 11.1). Построить развёртку боковой поверхности усечённой части цилиндра.

Решение: на рисунке 11.1 изображены прямой круговой цилиндр, основание которого принадлежит горизонтальной плоскости проекций и секущая плоскость Р общего положения. Поскольку секущая плоскость наклонена к оси цилиндра, то боковая поверхность цилиндра пересекается по эллиптической кривой.Форма сечения в этом случае зависит от того, пересекает ли плоскость Р основания цилиндра. В рассматриваемом случае секущая плоскость Р не пересекает оснований цилиндра. Это видно из того, что горизонтальная проекция нижнего основания не пересекается с горизонтальным следом плоскости Р, а горизонтальная проекция горизонтали , по которой плоскость Р пересекается с плоскостью верхнего основания, не пересекает его горизонтальную проекцию.

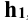
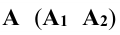
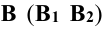
Для нахождения эллипса сечения плоскости Р с боковой поверхностью цилиндра находят сначала его низшую и высшую точки.

Эти точки являются концами большой оси эллипса сечения и лежат на линии наибольшего наклона плоскости Р к горизонтальной плоскости проекций. Следовательно, прямая АВ перпендикулярна к горизонтальному следу плоскости Р и пересекает ось цилиндра.

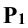
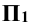
Для нахождения точек А и В проводят плоскость Σ, перпендикулярную к горизонтальному следу и проходящую через ось цилиндра. Эта плоскость перпендикулярна к плоскости . Затем находят линию пересечения плоскостей Р и Σ.

Боковая поверхность цилиндра является горизонтально проецирующей и поэтому проецируется на горизонтальную плоскость проекций в окружность. Так как отрезок АВ является частью линии пересечения плоскостей Р и Σ, а точки А и В лежат на боковой поверхности цилиндра, то горизонтальные проекции точек А и В должны лежать на одной окружности и на горизонтальной проекции прямой пересечения плоскостей Р и Σ. По горизонтальным проекциям точек А и В находят их фронтальные проекции, исходя из условия, что точки А и В лежат на найденной прямой пересечения плоскостей Р и Σ.

Для определения остальных точек эллипса сечения на цилиндрической поверхности выбирают ряд образующих. За первую образующую выбирают ту, на которой лежит точка А. Остальные образующие получают делением окружности (горизонтальной плоскости цилиндрической поверхности) на 12 равных частей (можно делить на другое количество частей). Затем находят точки пересечения образующих с плоскостью Р. В рассматриваемом примере все образующие перпендикулярны к горизонтальной плоскости проекций. Следовательно, горизонтальные проекции точек пересечения образующих с плоскостью Р совпадают с горизонтальными проекциями самих образующих.

Далее наносят горизонтальные проекции точек пересечения образующих с плоскостью Р (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) и находят фронтальные проекции этих точек, проводя через них горизонтали в плоскости.

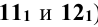
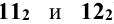
Кривая линия, ограничивающая фронтальную проекцию фигуры сечения, включает видимые и невидимые участки. Точки, являющиеся границей видимости кривой, лежат на очерковых образующих. Отмечают горизонтальные проекции этих точек () и находят фронтальные проекции (), проводя через эти точки в плоскости Р горизонтали. Полученные точки соединяют плавной кривой линией. Кривая от точки 12 через точки 10, А, 1, 2, 3, 4 до точки 11 на фронтальной плоскости проекций является видимой, а остальная часть — невидимой.

Видимую часть кривой обводят сплошной линией, а невидимую — штриховой. Малой осью эллипса сечения является отрезок 3 — 8, проецирующийся в натуральную величину на горизонтальную плоскость проекций. Натуральная величина малой оси эллипса в рассматриваемом примере равна диаметру цилиндра. Натуральную величину эллипса сечения строят путём совмещения плоскости Р с горизонтальной плоскостью проекций.

Развёртка боковой поверхности прямого кругового цилиндра, не усечённого плоскостью, представляет собой прямоугольник с основанием, равным длине окружности основания цилиндра, и высотой, равной высоте цилиндра. При построении развёртки боковой поверхности цилиндра, пересечённого плоскостью, на развёртке необходимо наносить точки, принадлежащие линии пересечения, и затем эти точки соединять плавной кривой линией (рис. 11.1).

Для этого на развёртке боковой поверхности цилиндра проводят 12 образующих, отстоящих друг от друга на равном расстоянии. За первую образующую рекомендуется выбирать ту, на которой лежит точка А. Затем наносят на все образующие последовательно точки А, 1, 2, 3, 4, 11, 5, В, 6, 7, 8, 9, 12, 10. Расстояние от этих точек до нижнего (или верхнего) основания проецируется на фронтальную плоскость проекций в натуральную величину. Соединив полученные точки плавной кривой линией, получают развёртку боковой поверхности усечённой части цилиндра.

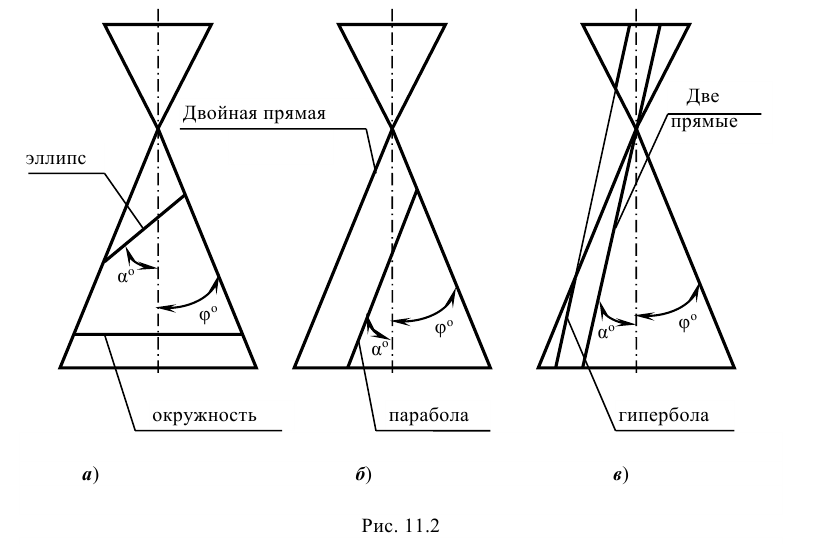
Задание: построить проекции и натуральную величину линии пересечения поверхности конуса плоскостью Р (рис. 11.3).

Решение: поверхность прямого кругового конуса относится к поверхностям вращения и является носителем кривых второго порядка: окружности, эллипса, параболы и гиперболы. Все эти кривые являются плоскими и, следовательно, могут быть получены в результате сечения конической поверхности плоскостью.

На рис. 11.2 приведены фронтальные проекции поверхности прямого кругового конуса, следы фронтально проецирующих секущих плоскостей и указан вид получаемой в сечении кривой. Можно установить признаки, обеспечивающие получение в сечении той или иной кривой второго порядка. Так, если обозначить угол наклона образующей конической поверхности к его оси через φ а угол между секущей плоскостью и той же осью через α , то можно утверждать, что при α > φ (рис. 11.2, а) в сечении получается эллипс (в частном случае, если α =90° — окружность), при α = φ (рис. 11.2, б) — парабола, и при α

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.