Таблица треугольников 5 класс (6 видео) | Курс школьной геометрии

Таблица виды треугольников
презентация к уроку (5 класс) по теме

Таблица треугольников по видам углов и сторон. Применяется при изучении темы «Треугольники», в коррекционной школе 8 вида.

Содержание

Скачать:
Предварительный просмотр:
Подписи к слайдам:
По теме: методические разработки, презентации и конспекты
Виды треугольников
Математика. 5 класс
Рисунки из треугольников
📽️ Видео

Видео:Математика 5 класс (Урок№28 - Треугольники.)Скачать

Скачать:

Вложение	Размер
tablica_vidy_treugolnikov_.ppt	135.5 КБ

Предварительный просмотр:

Видео:Треугольник и его виды. 5 классСкачать

Подписи к слайдам:

по сторонам по углам РАЗНОСТОРОННИЙ РАВНОБЕДРЕННЫЙ РАВНОСТОРОННИЙ ПРЯМОУГОЛЬНЫЙ (прямой угол) 90 ˚ ОСТРОУГОЛЬНЫЙ (острый угол) От 0 ˚ до 90 ˚ ТУПООУГОЛЬНЫЙ (тупой угол) От 90 ˚ до 180 ˚ Виды треугольников по углам и по сторонам.

Видео:ТРЕУГОЛЬНИК и его виды. §14 математика 5 классСкачать

По теме: методические разработки, презентации и конспекты

Урок геометрии по теме «Виды треугольников. Медианы, высоты, биссектрисы треугольника»

Урок геометрии по теме «Виды треугольников. Медианы, высоты, биссектрисы треугольника» целесообразно проводить в 7 классе при изучении темы «Равенство треугольников» (по учебнику «Геометри.

Урок геометрии в 5 классе школы VIII вида по теме:»Треугольник. Виды треугольников по углам»

Урок- презентация в 5 классе школы VIII вида по теме:»Треугольник. Виды треугольников по углам». Представлены задания на распознавание различных видов треугольников, выведение следствия из факта.

Урок по математике 5 класс «Треугольники. Виды треугольников»

Урок по математике в формате ФГОС.

Конспект урока математики в 6 классе «Треугольники. Виды треугольников»

Цели урока: Образовательные: познакомить учащихся с определением треугольника, его элементов, обозначением; видами треугольников.Развивающие: развивать пространственное воображение учащихся.

Обобщающий урок по теме «Треугольник. Виды треугольников»

Повторение, обобщение и систематизация первоначальных знаний учащихся по теме «Треугольник. Элементы треугольника. Виды треугольников».

Технологическая карта урока математики в 5 классе. Тема:»Треугольник. Виды треугольников»

Технологическая карта урока составлена по учебнику:Математика:5 класс: учебник для учащихся общеобразовательных учреждений/А.Г. Мерзляк, В.Б.Полонский, М.С.Якир.-М.:Вентана –Граф,2016.

Разработка урока по математике в 5 классе. Урок – изучение нового материала. Тема урока «Треугольник. Виды треугольника»

Цели урока: Образовательная: познакомить учащихся с определением треугольника, его элементов, обозначением; видами треугольников.Развивающая: развивать пространственное воображение учащихся, гео.

Видео:КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Виды треугольников

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.

Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).

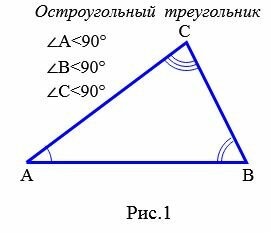Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).

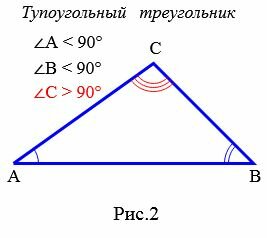Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).

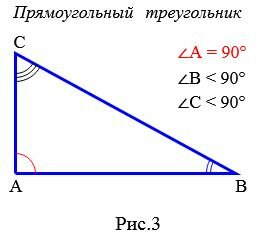Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).

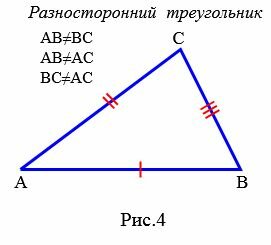Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).

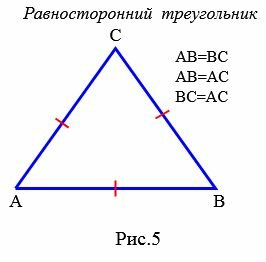Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).

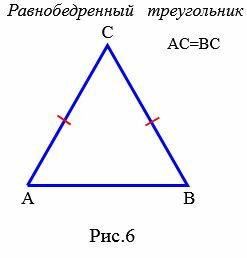В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.

Видео:Виды треугольниковСкачать

Математика. 5 класс

Конспект урока

Перечень рассматриваемых вопросов:

Треугольник – это геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых между собой.

Периметр треугольника – сумма длин всех сторон треугольника.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Среди всех многоугольников наименьшее число сторон и углов имеет треугольник. Он является простейшей фигурой, и казалось бы, его изучение не может быть интересным. Однако существует множество видов треугольников. О них мы и поговорим.

Отметим какие-нибудь три точки, не лежащие на одной прямой – например, А, В, С. Соединим их с помощью линейки. Получим геометрическую фигуру, которая называется треугольником. Отмеченные три точки А, В, С называются вершинами, отрезки АВ, ВС, АС – сторонами треугольника, а углы А, В, С – углами треугольника.

Все треугольники можно разделить на группы по сторонам:

— если равных сторон нет – это разносторонний треугольник;

— если две стороны равны – это равнобедренный треугольник;

— если все стороны равны – это равносторонний треугольник.

Треугольники можно разделить на группы в зависимости от углов:

— если есть тупой угол – это тупоугольный треугольник;

— если все углы острые – это остроугольный треугольник;

— если есть прямой угол – это прямоугольный треугольник.

Треугольники, соединяясь друг с другом, могут образовывать другие фигуры.

Попробуем нарисовать прямоугольный треугольник на листе в клетку. Мы знаем, что сторона стандартной клетки – пять миллиметров, следовательно, две клетки – это один сантиметр.

По сторонам клетки проведём отрезки заданной длины из одной точки. В нашем случае из точки А проведём отрезки длиной четыре и три сантиметра, что соответствует восьми и шести клеткам. На концах отрезков поставим точки В и С и соединим их между собой. Таким образом, мы построили прямоугольный треугольник АВС.

А теперь рассмотрим свойства треугольников. Одно из них – жёсткость. Это свойство заключается в том, что, если взять три рейки и соединить их попарно, то получится треугольник, изменить форму которого можно лишь сломав рейку.

Рассмотрим ещё одно свойство треугольников. Оно заключается в том, что длина каждой стороны треугольника всегда меньше суммы двух других сторон.

Это свойство можно использовать для проверки возможности построения треугольника по определённым сторонам. То есть, если свойство не выполняется, то такого треугольника не может быть.

Если мы знаем стороны треугольника, то можем найти его периметр как сумму длин всех его сторон. Например, периметр треугольника АВС – это сумма сторон АВ, АС и ВС.

Измерим с помощью линейки стороны треугольника и рассчитаем его периметр.

По результатам измерения стороны, соответственно, равны пяти, шести и семи сантиметрам.

Значит, периметр равен восемнадцати сантиметрам, то есть сумме всех сторон.

Говоря о треугольниках, стоит упомянуть, что они бывают как одинаковыми, так и разными. Определить, равные или разные треугольники, можно способом наложения. Если треугольник полностью накладывается на другой треугольник, такие треугольники равны. В противном случае треугольники не будут равными.

Видео:Виды треугольниковСкачать

Рисунки из треугольников

Многие люди, как маленькие, так и взрослые, очень любят рисовать. Но иногда одного желания рисовать недостаточно. Для того чтобы облегчить процесс создания простейших картинок, инженер Эриф Мд. Вейлиула Байан, разработчик инновационного контента для детей, создал схемы, по которым, имея базовые навыки работы с чертёжными инструментами, можно создать милые и забавные картинки с животными и птицами.

Похожие схемы частично есть в открытом доступе, поэтому каждый желающий может приобщиться к миру изобразительного искусства через поэтапное прорисовывание простых картинок.

№ 1. В треугольнике все стороны равны 15 см. Чему равен периметр треугольника?

Решение: для нахождения периметра используем формулу Р = АВ + АС + ВС.

Так как у этого треугольника стороны равны, то Р = 15 см + 15 см + 15 см = 45 см

№ 2. Сопоставьте треугольники с их видами (по углам).

Решение: в задаче требуется сопоставить треугольники со следующими видами по углам: остроугольный, прямоугольный, тупоугольный. Согласно определению, прямоугольный треугольник имеет один угол 90 градусов: этому треугольнику соответствует второй треугольник. А тупоугольный треугольник имеет один угол больше 90 градусов: он отображён третьим по счёту. Как мы знаем, остроугольный треугольник имеет три угла меньше 90 градусов, так что в этом случае подходит треугольник, изображённый первым слева.