Таблица 20 касательная к окружности 115 решение (4 видео)

Таблица 20 касательная к окружности 115 решение

Вопрос по геометрии:

Помогите пж ( 8 класс) Касательная окружность

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Содержание

Как написать хороший ответ?
Касательная к окружности. Решение задач
Просмотр содержимого документа «Касательная к окружности. Решение задач»
Касательная к окружности
Касательная к окружности, секущая и хорда — в чем разница
Свойства касательной к окружности
Задача
Задача 1
Задача 2
Задача 1
Задача 2
Задача 1
Задача 2
🎬 Видео

Ответы и объяснения 1

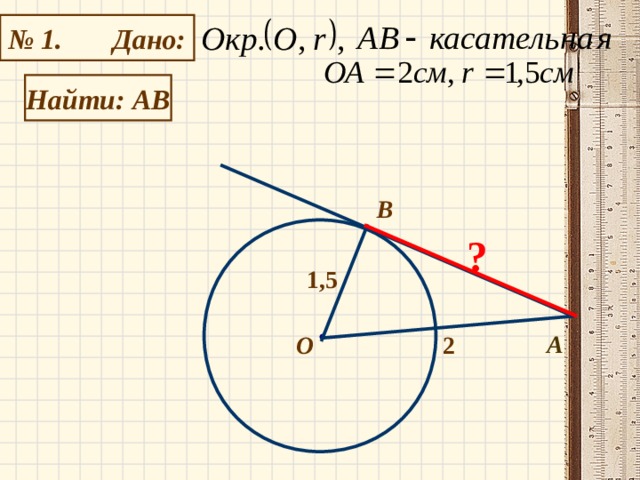
№2.
Дано:
Окр. О;
Касательные к окр. NM и KM из точки М;
ON = 9;
OM = 18;
Угол NMK — ?
——
Решение:
Sin NMO = ON/OM = 9/18 = 1/2. Угол NMO = 30°.
Известно, что отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Значит, угол NMO равен углу OMK. Угол NMK равен сумме углов OMK и NMO.
Угол NMK = 30°+30°=60°.
Ответ: угол NMK = 60°.

№3.
Дано:
Окр. О;
Касательная AC, AC пересекает Окр. = А;
АВ — хорда;
OA = AB;
Угол BAC — ?
——
Решение:
Проведём радиус OB. Треугольник АОВ — равносторонний, т.к. ОА — радиус, ОВ — радиус, и АВ равен ОА.
Угол А равен углу В, равен углу О, равен 180°/3 = 60°.
Т.к. АС — касательная, то угол OAC = 90° = сумме углов OAB и BAC.
Угол BAC = угол OAC — угол OAB = 90° — 60° = 30°.
Ответ: угол BAC = 30°.

№6.
Дано:
Окр. О;
Касательные МК и NK из точки К;
ОК = 6;
Угол MON = 120°;
MK, NK — ?
——
Решение:
Т.к. отрезки касательных к окружности, проведённых из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности, то MK = NK и угол MKO равен углу OKN.
Угол MON составляет сумму равных углов MKO и OKN. Значит, Угол MKO равен углу OKN, равен 120°/2 = 60°.
tg MKO = OM/MK; tg 60° = √3; MK = ON = OM/tg30° = 6/√3 = 6√3/3 = 2√3
Ответ: MK = ON = 2√3.

№7.
Дано:
Окр. А;
Треугольник АСВ;
D принадлежит AB, AD — радиус;
Е принадлежит АС, АЕ — радиус;
CD — касательная;
CD = 12;
AB = 25;
Угол ACB = 90°;
AE — ?
——
Решение:
Т.к. CD — касательная, то в тр-ке ACB, CD — высота.
Известно, что высота в прямоугольном треугольнике, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой. Значит, CD = √(AD*DB).
Т.к. AD = r, а AB = 25, то DB = 25-r.
Отсюда: CD = √(r*(25-r)), 12 = √(r*(25-r)).
r*(25-r) = 144,
r² — 25r + 144 = 0;
D = 635 — 576 = 49, √D = ±7;
1) r = (25+7)/2 = 16;
2) r = (25-7)/2 = 9.
Ответ: AE = 16, либо AE = 9.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Касательная к окружности. Решение задач

Просмотр содержимого документа
«Касательная к окружности. Решение задач»

8 класс. Геометрия

Решение задач по теме «Касательная к окружности»

Учитель математики: Барсукова И.Е.

Повторение теоретического материала

Как вы думаете, сколько общих точек могут иметь прямая и окружность?

r две общие точки одна общая точка не имеют общих точек Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку . Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки . Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек . » width=»640″

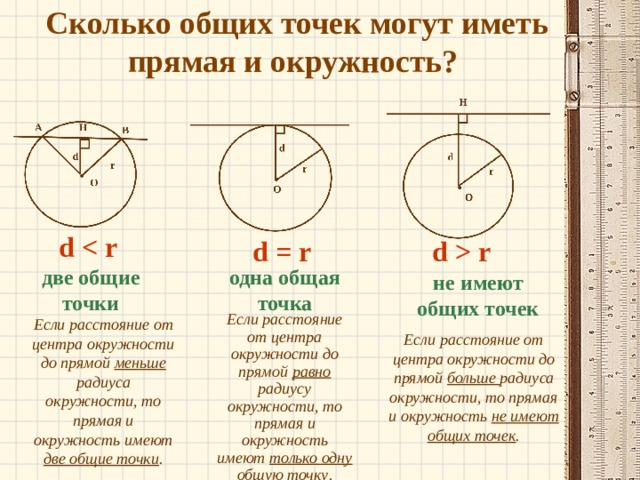
Сколько общих точек могут иметь прямая и окружность?

две общие точки

одна общая точка

не имеют общих точек

Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку .

Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки .

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .

Касательная к окружности

Определение: П рямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

m – касательная к окружности с центром О

М – точка касания

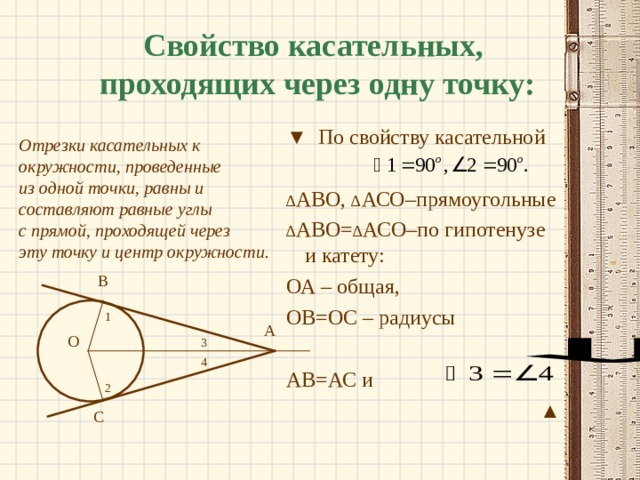
Свойство касательных, проходящих через одну точку:

Отрезки касательных к

из одной точки, равны и

составляют равные углы

с прямой, проходящей через

эту точку и центр окружности.

▼ По свойству касательной

∆ АВО= ∆ АСО–по гипотенузе и катету:

Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является к асательной.

окружность с центром О

m – прямая, которая проходит через точку М

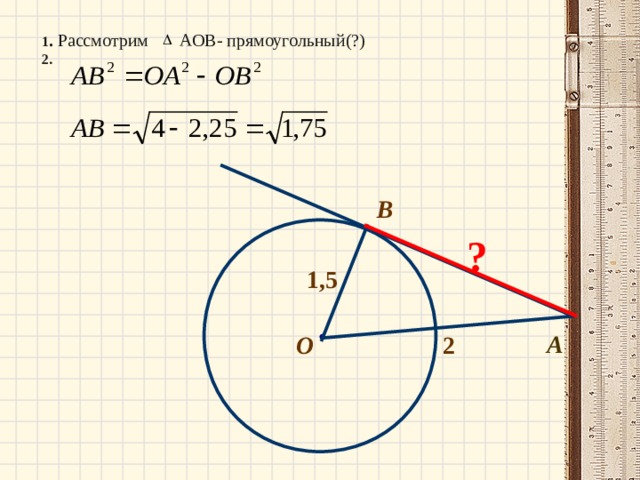
1 . Рассмотрим АОВ- прямоугольный(?)

Видео:НЕКОТОРЫЕ СВОЙСТВА ОКРУЖНОСТИ. КАСАТЕЛЬНАЯ к окружности. §20 геометрия 7 классСкачать

Касательная к окружности

О чем эта статья:

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

окружность с центральной точкой А;
прямая а — касательная к ней;
радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°