Окружность

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.

Часть плоскости, ограниченная окружностью называется кругом.

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Основные термины

Касательная

Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойства касательной

1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Хорда

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.

Свойства хорд

1. Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключенные между параллельными хордами, равны.

Если две хорды окружности, AB и CD пересекаются в точке M , то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Видео:Окружность. 7 класс.Скачать

Свойства окружности

1. Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку ( касательная ); иметь с ней две общие точки ( секущая ).
2. Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
3. Точка касания двух окружностей лежит на линии, соединяющей их центры.

Теорема о касательной и секущей

Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC 2 = MA•MB .

Теорема о секущих

Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Углы в окружности

Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.

Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.

Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Свойства углов, связанных с окружностью

1. Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.

Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на диаметр, равен 90°.

Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.

Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Длины и площади

1. Длина окружности C радиуса R вычисляется по формуле:

Площадь S круга радиуса R вычисляется по формуле:

Длина дуги окружности L радиуса R с центральным углом ,измеренным в радианах, вычисляется по формуле:

Площадь S сектора радиуса R с центральным углом в радиан вычисляется по формуле:

Видео:Доказать, что точки лежат на одной окружностиСкачать

Вписанные и описанные окружности

Окружность и треугольник

• центр вписанной окружности — точка пересечения биссектристреугольника, ее радиус r вычисляется по формуле:

где S — площадь треугольника, а — полупериметр;

центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус R вычисляется по формуле:

здесь a, b, c — стороны треугольника, — угол, лежащий против стороны a , S — площадь треугольника;

Окружность и четырехугольники

• около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:

в четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:

• около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
• около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне;
• в параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Признак принадлежности четырёх точек одной окружности

Признак принадлежности четырёх точек одной окружности

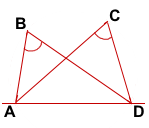
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.

Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,

Доказать: точки A, B, C, D лежат на одной окружности

Обозначим ∠ABD=∠ACD=α.

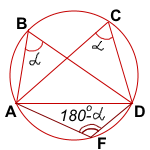
Опишем около треугольника ABD окружность.

Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.

Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:

Рассмотрим четырехугольник ACDF.

Отсюда следует, что четырёхугольник ABDF — вписанный.

Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

📺 Видео

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

Тригонометрическая окружность. Как выучить?Скачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Условие принадлежности четырёх точек одной окружностиСкачать

2020 точка О центр окружности на которой лежат точки A B и C известно что Угол ABC равен 62 градусаСкачать

Первое условие принадлежности четырех точек одной окружностиСкачать

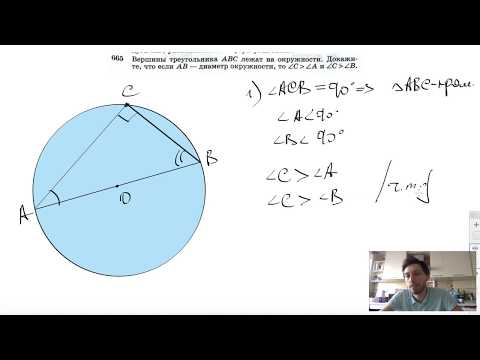
№665. Вершины треугольника ABC лежат на окружности. Докажите, что если АВ — диаметр окружностиСкачать

5 класс, 22 урок, Окружность и кругСкачать

Окружность. Круг. 5 класс.Скачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

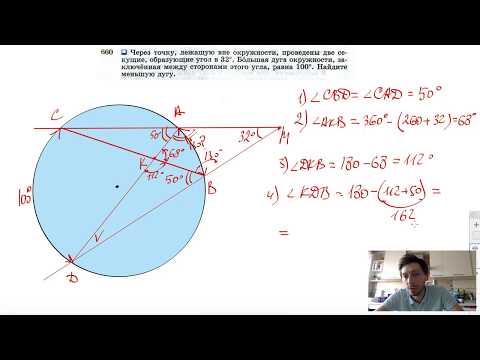
№660. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать