Сумму данных векторов используй параллелепипед и повтори знания о векторах плоскости (4 видео)

Правило параллелепипеда. Разложение вектора

Вы будете перенаправлены на Автор24

Содержание

Правило параллелепипеда
Разложение вектора по двум неколлинеарным векторам
Сумма нескольких векторов
Правило многоугольника или правило цепи
Свойство сочетательности
Правило параллелепипеда
Геометрия. 10 класс
📸 Видео

Видео:Правило параллелепипеда для векторовСкачать

Правило параллелепипеда

Для правила сложения трех векторов рассмотрим следующую задачу.

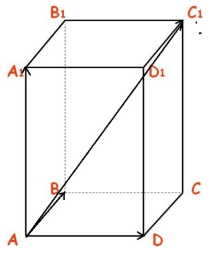
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$

Доказательство.

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$

Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.

Видео:10 класс, 44 урок, Правило параллелепипедаСкачать

Разложение вектора по двум неколлинеарным векторам

Вспомним сначала, какие векторы называются компланарными.

Два вектора, которые параллельны одной плоскости называются компланарными.

Произвольный вектор $overrightarrow

$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow $ и $overrightarrow $ с единственными коэффициентами разложения.

Математически это можно записать следующим образом

Доказательство.

Существование: Пусть нам даны три некомпланарных вектора $overrightarrow , overrightarrow $ и $overrightarrow $. Выберем произвольную точку $O$ и построим следующие векторы:

[overrightarrow =overrightarrow, overrightarrow =overrightarrow, overrightarrow =overrightarrow и overrightarrow

=overrightarrow]

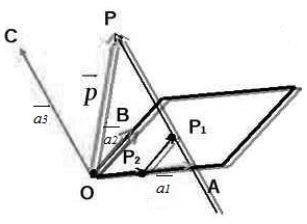
Рассмотрим следующий рисунок:

Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Тогда, получаем, что

Существование разложения доказано.

Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow

$ по векторам $overrightarrow , overrightarrow $ и $overrightarrow $:

Вычтем эти разложения друг из друга

Из этого получаем

Теорема доказана.

Видео:Вектор. Сложение и вычитание. 9 класс | Математика Скачать

Сумма нескольких векторов

Сумма нескольких векторов а ₁, а ₂, а ₃, … , а _n, это вектор, получающийся после ряда последовательных сложений: к вектору а ₁ прибавляется вектор а ₂, к полученному вектору прибавляется вектор а ₃ и т.д.

Из определения вытекает такое построение

Видео:Как выразить вектор через данные векторы параллелограмма. Векторы на плоскости. Геометрия 8-9 классСкачать

Правило многоугольника или правило цепи

Из произвольного начала О строим вектор ОА ₁ = а ₁, из точки А ₁, как из начала, строим вектор А ₁ А ₂ = а ₂, из точки А ₂ строим вектор А ₂ А ₃ = а ₃ и т.д. Вектор ОА _n (на рисунке n = 6) есть сумма векторов а ₁, а ₂, … , а _n.

Видео:Сложение векторов. 9 класс.Скачать

Свойство сочетательности

Слагаемые векторы можно группировать как угодно.

Так, если найти сначала сумму векторов

и к ней прибавить вектор а ₁ ( ОА ₁), то получим то же вектор:

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Правило параллелепипеда

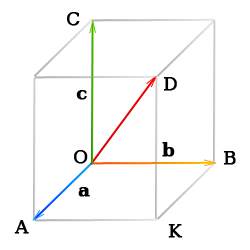
Если три вектора а , b , с после приведения к общему началу не лежат в одной плоскости, то сумму а + b + c можно найти таким построением:

Из любого начала О строим векторы ОА = а , ОВ = b , ОС = с , на отрезках ОА , ОВ , ОС , как на ребрах, строим параллелепипед. Вектор диагонали OD есть сумма векторов a , b , и c (так как ОА = а , АК = ОВ = b , KD = OC = c и OD = OA + AK + KD ).

К векторам, которые (после приведения к общему началу) лежат в одной плоскости, это построение неприменимо.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Геометрия. 10 класс

Сумма векторов

В кубе назовите вектор, равный сумме $overrightarrow+overrightarrow <B_C_>+overrightarrow<DD_> $

Вектор в пространстве

Установите соответствие между выражением и вектором $Х$

Длина вектора

Дано: АВ = 3 ВС = 4 СС₁ = 12

Длина вектора АС₁ =

Длина вектора

Диагонали параллелепипеда пересекаются в точке О.

Варианты ответа (введите порядковый номер):

Вектор в пространстве

Упростите выражение и выберите правильный результат преобразования:

Вектор в пространстве

В тетраэдре ABCD точка Е — середина АD.

Докажите, что $overrightarrow=frac(overrightarrow+overrightarrow)$

Сложим полученные равенства $overrightarrow+overrightarrow+overrightarrow+overrightarrow=2overrightarrow$

Так как $overrightarrow+overrightarrow=0$, то $overrightarrow+overrightarrow=2overrightarrow$, значит $overrightarrow=frac(overrightarrow+overrightarrow)$