Сумма медиан треугольника равна

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Видео:8. Медиана треугольника и её свойства.Скачать

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Видео:№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

• AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
• AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Сумма векторов медиан треугольника равна

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Точка O — центр тяжести ( точка пересечения медиан) Доказать что сумма векторов OA + OB + OC равна нулю.

Продлим OC1 через C1 до точки D так что OC1 = C1D.
Тогда OADB — параллелограмм, вектора AD = OB, вектора DO = OC.
В треугольнике OAD имеем: OA + AD + DO = 0,
Эта сумма = OA + OB + OC.

Если подвесить этот треугольник за центр тяжести, его можно будт расположить параллельно земле и он не выйдет из этого состояния. Если представить, что вся масса треугольника сосредоточена в тех трёх векторах, то сумма любых двух должна уравновешивать третий, то есть действительно, сумма всех трёх равна нулю.

Видео:Точка пересечения медиан в треугольникеСкачать

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Задачник «Векторный метод решения задач»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:🔥 Свойства МЕДИАНЫ #shortsСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Задачник «Векторный метод решения задач»

Составила: Казакова Ольга Сергеевна,

учитель математики МОУ «СОШ № 75» г. Саратова.

Данный задачник предназначен для изучения тем: «Векторы», «Действия с векторами», «Векторный метод решения задач». Инструктивное изложение материала, при постоянной практической пробе, даёт возможность изучить темы самостоятельно.

№ 1.Заполните таблицу. Основные понятия.

Решение и изображение

1)На плоскости отметьте точки A и B , постройте отрезок AB ;

2)На отрезке AB пусть точка A будет началом, а точка B – концом. Укажите стрелкой в конце отрезка направление из начала в конец. Вы получили отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, то есть получили направленный отрезок или вектор .

3)Построен вектор , его можно обозначить и однострочной латинской буквой, например, , которая записывается над изображением вектора.

Сколько векторов можно провести, выбирая начало и конец среди данных на плоскости:

2)трёх точек, не лежащих на одной прямой;

3)четырёх точек, не лежащих на одной прямой?

Отметьте на плоскости любую точку и обозначьте её, например, заглавной буквой M . Вы построили нулевой вектор, его начало и конец совпадают.

Обозначение нулевого вектора: или символом .

1)Постройте отрезок AB , длина которого 4 см;

2)Постройте вектор .

Длиной или модулем ненулевого вектора называется длина отрезка AB .

Обозначение: = AB = 4.

Чему равна длина нулевого вектора?

3)Постройте вектор , длиной 7 см.

1)Постройте параллельные прямые p и m .

2)На прямой p постройте:

а)вектор , произвольной длины и направления;

б)вектор , произвольной длины и направления;

3)На прямой m постройте: вектор , произвольной длины и направления.

Ненулевые векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых.

Нулевой вектор считается коллинеарным любому вектору.

4)Выпишите попарно коллинеарные векторы.

5)Постройте и обозначьте два произвольных вектора, которые являются не коллинеарными вектору . Будут ли они являться коллинеарными векторам , ?

Постройте два коллинеарных вектора.

Полученные векторы направлены одинаково или противоположно?

Если одинаково, то вы построили сонаправленные векторы. Обозначение:

 .

Если противоположно, то вы построили противоположно направленные векторы. Обозначение:  .

Начертите параллелограмм ABCD . Проведите векторы, начало и конец которых совпадают с какими-то двумя вершинами параллелограмма. Сколько существует пар векторов, которые являются:

1)коллинеарными друг другу;

Постройте векторы и , так, чтобы:

1)  ;

2) .

Вы построили равные векторы.

Векторы называются равными , если они сонаправлены и их длины равны.

№ 2.Заполните таблицу. Операции над векторами.

Решение и изображение

На плоскости произвольно выберите точку A , приняв её за начало, проведите вектор , произвольной длины и направления. Таким образом, вы отложили вектор от точки A .

Можно отложить от другой точки плоскости, вектор, равный данному вектору ?

Допустим, что вектор ненулевой, а точки A и B – его начало и конец.

1)Через произвольно взятую точку M плоскости проведите прямую p , параллельную AB (если M – точка прямой AB , то в качестве прямой p возьмём саму прямую AB ).

2)На прямой p отложите два противоположно направленных вектора и , длины которых равны отрезку AB .

Среди построенных векторов выберите тот, что сонаправлен с вектором , он и будет являться искомым вектором, равным вектору . К тому же такой вектор только один, что следует из построения.

А если вектор – нулевой? Ответьте самостоятельно.

Итак, от любой точки M можно отложить вектор, равный данному вектору , и при том только один.

1)Векторы и .

2)Произвольная точка A .

3)От точки A отложите вектор , равный вектору .

4)От точки B отложите вектор , равный вектору .

5)Вектор .

Вы, таким образом, выполнили построение сложения векторов и по правилу треугольника . Вектор называется суммой векторов и .

Докажем, что если и , то .

Рассмотрим случай, когда точки A , B , , точки B , C , и точки A , C , не лежат на одной прямой (остальные случаи рассмотрите самостоятельно).

а) ;

б) ;

в)Соединим точки A и , B и , C и ;

2)  – параллелограмм  ;

3)  – параллелограмм  ;

4)Из 2) и 3)   – параллелограмм;

5)Значит, . Доказано.

Вывод: при необходимости можно работать как с данными векторами, так и с равными им.

Законы сложения векторов.

Для любых векторов , и справедливы равенства:

(переместительный закон)

(сочетательный закон)

Доказательство законов проведите самостоятельно, опираясь на подсказки:

Для доказательства первого закона можете достроить треугольник до параллелограмма и работать как с самими векторами, так и с равными им.

Для доказательства второго закона достаточно несколько раз применить правило треугольника для сложения векторов, последовательно отложенных от концов предыдущих векторов.

1)Произвольная точка A ;

2)Неколлинеарные векторы и ;

3) От точки A отложите вектор , равный вектору .

4)От точки A отложите вектор , равный вектору .

5)Постройте параллелограмм ABCD ;

6) .

Вы построили сложение векторов и по правилу параллелограмма сложения неколлинеарных векторов.

Как сложить несколько векторов?

Последовательное применение правила треугольника для сложения векторов даёт возможность сложить любое количество векторов. Причём порядок сложения не важен. Сложение нескольких векторов производится следующим образом: два вектора складываются, получившаяся сумма складывается с третьим и т.д.

Выполните сложение пяти любых векторов, используя то, что несколько векторов можно расположить таким образом: первый вектор откладывается от любой точки, второй – от конца первого и т.д. Сумма всех векторов – вектор, направленный от начала первого вектора к концу последнего.

Вы выполнили построение сложения нескольких векторов, пользуясь правилом многоугольника .

Подумайте, чему будет равна сумма векторов, если начало первого вектора совпадает с концом последнего?

Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору .

Вектор называется противоположным вектору , если векторы и имеют равные длины и противоположно направлены. Обозначение: . .

Докажите, что . Для этого воспользуйтесь определением разности векторов и прибавлением к обеим частям равенства вектора.

На прямой p от любой точки O отложите вектор , от конца вектора отложите вектор . Длина построенного суммарного вектора, равна или .

Произведением ненулевого вектора на число k называется такой вектор , длина которого равна , причём векторы и сонаправлены при k  0 и противоположно направлены при k .

Произведением нулевого вектора на любое число считается нулевой вектор.

Из определения следует:

1)произведение любого вектора на число нуль есть нулевой вектор;

2)для любого числа k и любого вектора векторы и коллинеарны.

Свойства умножения вектора на число.

Для любых чисел k , l и любых векторов , справедливы равенства:

(сочетательный закон)

(первый распределительный закон)

(второй распределительный закон)

На прямой p от произвольно выбранной точки O отложите: вектор , длиной 1 см; вектор , сонаправленный с вектором , длиной 2 см; вектор , противоположно направленный с вектором , длиной 3 см.

Попробуем выразить векторы и через вектор .

Во сколько раз длины этих векторов отличаются от длины вектора ?

; ;

 ,  , т. е. векторы , и коллинеарны друг другу, значит, можно воспользоваться леммой.

Если векторы и коллинеарны и , то существует такое число k , что .

Итак, можем выразить: , .

От произвольной точки O отложите векторы и , и – произвольные данные векторы. Если и не являются сонаправленными, то лучи OA и OB образуют угол AOB , градусную меру которого обозначьте буквой α. Будем говорить, что угол между векторами и равен α. Обозначение: .

Если  , то

Если , то векторы и называются перпендикулярными.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Напишите формулу скалярного произведения для случаев, когда:

;

;

.

Сделайте вывод, о том, в каком случае скалярное произведение двух векторов равно нулю.

Напишите формулу скалярного произведения для случая, когда вектор скалярно умножается на себя. В этом случае скалярное произведение называется скалярным квадратом . Обозначение: .

Итак, перечислите все операции над векторами.

№ 3.Решая задачи, заполните пустые ячейки в таблице.

k , что ,

точки M и N совпадают

точка C принадлежит прямой AB

, или
, или

точка С – середина отрезка AB

точка D разбивает отрезок AC так, что AD : DC = m : n

Заполняя таблицу, вы пользовались векторным методом решения задач.

Векторный метод – один из наиболее общих методов решения геометрических задач.

Для решения задач элементарной геометрии с помощью векторов необходимо, прежде всего, научиться «переводить» условие геометрической задачи на «векторный» язык. После такого перевода осуществляются алгебраические вычисления с векторами, а затем полученное снова «переводится» на «геометрический» язык. В этом и состоит сущность векторного метода решения геометрических задач.

Далее вам необходимо самостоятельно решать задачи. После решения каждой задачи делайте вывод о её значимости. Если результат задачи возможно использовать для решения других, то заносите его в таблицу № 3. Таким образом, вы получите набор базовых задач, на основании которых решаются более сложные.

1)Докажите, что средняя линия треугольника параллельна его третьей стороне и равна её половине.

2)Докажите, что средняя линия трапеции параллельна её основанию и её длина равна полусумме длин её оснований.

3)Если средняя линия четырёхугольника равна полусумме длин её оснований (сторон, не имеющих общей точки со средней линией), то этот четырёхугольник является трапецией или параллелограммом.

4)Около окружности описана равнобочная трапеция ABCD . Точки E и K – точки касания этой окружности с боковыми сторонами AB и CD . Докажите, что отрезок EK параллелен основаниям трапеции.

5)Докажите, что биссектриса угла треугольника делит его сторону на отрезки, пропорциональные прилежащим сторонам. Выразите биссектрису через угол треугольника, который она делит пополам, и через стороны этого угла.

6)Если точки M и N делят отрезки AB и CD соответственно в равных отношениях так, что AM : MB = CN : ND = m : n , то выполняется равенство: .

7)В треугольнике ABC через M обозначена точка пересечения медиан. Докажите, что .

8)Пусть M – точка пересечения медиан треугольника ABC , O – произвольная точка. Докажите, что .

9)Пусть H – точка пересечения высот треугольника ABC , O – центр описанной окружности. Докажите, что .

10)Докажите, что три точки A , B , C ( A ≠ B ) лежат на одной прямой тогда и только тогда, когда имеет место равенство, , в котором α+β=1, где O – некоторая точка.

11)Докажите, что центр описанной окружности

12)Докажите, что если точки пересечения диагоналей четырёхугольника и середины двух его противоположных сторон лежат на одной прямой, то этот четырёхугольник – трапеция или параллелограмм.

13)Докажите, что медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.

14)Докажите, что биссектрисы треугольника пересекаются в одной точке.

15)Докажите, что высоты треугольника пересекаются в одной точке.

16)Докажите, что четырёхугольник является параллелограммом тогда и только тогда, когда его диагонали в точке пересечения делятся пополам.

17)Докажите, что в произвольном четырёхугольнике средние линии (т. е. отрезки, соединяющие середины противоположных сторон) точкой их пересечения делятся пополам.

18)Найти косинус угла между диагоналями прямоугольника, стороны которого равны a и b .

19)Докажите, что диагонали ромба взаимно перпендикулярны.

20)Докажите, что вписанный угол, опирающийся на диаметр окружности, — прямой.

21)Докажите, что если в треугольнике длины его сторон a , b , c связаны соотношением , то угол этого треугольника, лежащий против стороны длины c , — прямой.

22)Даны стороны a , b , c треугольника. Найдите медианы , , , проведённые к этим сторонам.

23)В треугольнике со сторонами a , b , c найти длину высоты , опущенную на сторону c .

24)В треугольнике со сторонами a , b , c найти длину биссектрисы , проведённой к стороне c .

25)Докажите, что сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин всех его сторон.

26)Докажите, что сумма квадратов длин диагоналей трапеции равна сумме квадратов длин её боковых сторон плюс удвоенное произведение длин оснований.

27)Доказать, что большей медиане треугольника соответствует меньшая сторона и обратно.

28)Докажите, диагонали прямоугольника равны между собой.

29)Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен их полуразности.

30)В четырёхугольнике ABCD прямая, проведённая через вершину A параллельна стороне BC , пересекает диагональ BD в точке M , а прямая проведённая через вершину B параллельно стороне AD , пересекает диагональ AC в точке N . Докажите, что MN || DC .

31)Четыре окружности радиуса R пересекаются по три в точках M и N , и по две в точках A , B , C , D . Докажите, что ABCD – параллелограмм.

32)Пусть K , L , M , N – середины отрезков AB , BC , CD , DE пятиугольника ABCDE , а точки P и Q – середины отрезков KM и LN соответственно. Докажите, что отрезок PQ в четыре раза меньше стороны AE и параллелен ей.

33)В плоскости даны четырёхугольник ABCD и точка M . Докажите, что точки, симметричные точке M относительно середин сторон этого четырёхугольника, являются вершинами параллелограмма.

34)На диагоналях AC и CE правильного шестиугольника ABCDEF взяты точки M и N соответственно, такие, что AM : AC = CN : CE = λ. Известно, что точки B , M , N лежат на одной прямой. Найдите λ.

35)Дан параллелограмм ABCD ( AD || BC , AB || CD ). На стороне AD выбрана точка K , а на AC – точка L так, что 5 AK = AD , 6 AL = AC . Докажите, что KL || BL и найдите отношение их длин.

36)Точки M и K на сторонах AB и BC треугольника ABC таковы, что AM : MB =3:4, CK : KB =2:3. Отрезки AK и CM пересекаются в точке N . Найдите отношение AN : NK .

37)Точка K на стороне AC и точки L , M на стороне BC треугольника ABC таковы, что AK : KC = CL : LB = BM : MC =1:2, N – середина стороны AC . Найти отношение, в котором точка пересечения отрезков KL и MN делит отрезок KL .

38)Через середину E медианы треугольника ABC проведена прямая AE , пересекающая сторону BC в точке F . Вычислить: AE : EF и CF : FB .

39)Дан параллелограмм ABCD . Точка M делит сторону AD в отношении p , т. е. AM : MD = p ; точка N делит сторону DC в отношении q , т. е. DN : NC = q . Прямые BM и AN пересекаются в точке S . Вычислить отношения AS : SN и BS : SM .

40)В параллелограмме ABCD сторона AD разделена на n равных частей и первая точка деления M (считая от A ) соединена с B . В каком отношении делит точка N диагональ AC и отрезок MB ?

41)В треугольнике ABC проведена медиана CM . Прямая l пересекает отрезки CA , CM , CB в точках , , соответственно. Докажите равенство .

42)На сторонах AC и BC треугольника ABC взяты точки M и D так, что AM = AC , BD = BC , а на прямой AD – точка N так, что AN = AD . Доказать, что точки M , N и B лежат на одной прямой. Какую часть от отрезка MB составляет отрезок MN ?

43)На стороне AD и диагонали AC параллелограмма ABCD взяты точки M и N так, что AM = AD , AN = AC . Доказать, что точки M , N и B лежат на одной прямой. В каком отношении делит точка N отрезок MB ?

44)На стороне AB треугольника ABC дана точка P , через которую проведены прямые параллельно его медианам A и A и пересекающие соответственно стороны треугольника в точках и . Докажите, что середина отрезка (точка E ), а также точка P и точка G пересечения медиан треугольника лежат на одной прямой и найдите отношение длин отрезков EG и EP .

45)Докажите, что точки пересечения диагоналей трапеции, боковых сторон, а также середины оснований лежат на одной прямой.

46)Через точку P – внутреннюю точку параллелограмма ABCD – проведены прямая KM || AD и прямая LN || AB , пересекающие стороны AB , BC , CD , DA параллелограмма в точках K , L , M , N соответственно. Q – точка пересечения средних линий четырёхугольника KLMN , S – точка пересечения диагоналей параллелограмма ABCD . Докажите, что Q – середина отрезка PS .

47)Пусть , , – середины сторон BC , AC , AB треугольника ABC . Доказать, что точки пересечения медиан треугольника ABC и треугольника совпадают.

48)Пусть ABCDEF – произвольный шестиугольник и U , V , W , X , Y , Z – середины его сторон. Докажите, что центры тяжести (т. е. точки пересечения медиан) треугольника UWY и треугольника VXZ совпадают.

49)Докажите, что прямая, соединяющая середины оснований трапеции, и продолжения боковых сторон трапеции пересекаются в одной точке.

50)На сторонах параллелограмма заданы точки, которые делят стороны в одном и том же отношении (в каком-либо одном направлении обхода). Докажите, что точки деления служат вершинами параллелограмма, а центры этих параллелограммов совпадают.

51)На сторонах треугольника заданы точки, которые делят стороны в одном и том же отношении (в каком-либо одном направлении обхода). Докажите, что точки пересечения медиан данного треугольника и треугольника, имеющего вершинами точки деления, совпадают.

52)В треугольнике ABC длины сторон связаны соотношением . Докажите, что медианы, проведённые к сторонам AC и BC , взаимно перпендикулярны.

53)Найдите косинус угла между медианами прямоугольного равнобедренного треугольника, проведёнными к его катетам.

54)Найти косинус угла между медианами равнобедренного треугольника, проведёнными к его боковым сторонам, при условии, что угол при вершине равен α.

55)Найти косинус угла при вершине равнобедренного треугольника, если медианы, проведённые к его боковым сторонам, а) перпендикулярны; б) образую угол .

56)В треугольнике две стороны равны 2 и 4, а угол между ними равен . Найти угол ψ между короткой стороной и медианой, проведённой к третьей стороне.

57)В окружности с центром O радиуса r вписан четырёхугольник ABCD . Доказать, что если , то диагонали четырёхугольника взаимно перпендикулярны.

58)В прямоугольнике ABCD опущен перпендикуляр BK на диагональ AC . Точки M и N – середины отрезков AK и CD соответственно. Докажите, что угол BMN прямой.

59)На стороне AB треугольника ABC с углом ABC , равным α , расположена точка K , причём AK = BC . Пусть P – середина BK , M – середина AC . Найдите угол APM .

60)Точка K – середина стороны AB квадрата ABCD , а точка M лежит на диагонали AC , причём AM : MC = 3 : 1. Докажите, что угол KMD равен .

61)На сторонах AB и AC треугольника ABC во внешнюю сторону построены квадраты AMNB и CKLA . Докажите, что медиана AP треугольника ABC перпендикулярна прямой ML .

62)На стороне AB треугольника ABC дана точка D . Выразить расстояние CD через длины сторон данного треугольника a , b , c и расстояния AD = m и DB = n .

63)Выразить расстояние от заданной точки O до точки M пересечения медиан треугольника ABC через длины сторон треугольника BC = a , AC = b , AB = c и расстояния от точки O до вершин треугольника OA = , OB = , OC = .

64)В параллелограмме ABCD точка K – середина стороны BC , а точка M – середина стороны CD . Найдите AD , если AK = 6, AM = 3,  KAM = .

Список использованной литературы

Атанасян Л.С. и др. Геометрия. Учебник для 7-9 кл. общеобразовательных учреждений. – М.: Просвещение, 2003.

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10-11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни. – М.: Просвещение, 2009.

Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Шестаков С.А., Юдина И.И. Планиметрия. Пособие для углубленного изучения математики – М.: ФИЗМАТЛИТ, 2005.

Василевский А.Б. Методы решения геометрических задач. – Минск: Вышэйш. школа, 1965.

Габович И.Г. Алгоритмический подход к решению геометрических задач. – М.: Просвещение, 1996.

Гордин Р.К. Геометрия. Планиметрия 7-9 кл. – М.: МЦНМО, 2006.

Готман Э.Г., Скопец З.А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9 и 10 кл. – М.: Просвещение, 1979.

Гусев В. А. и др. Практикум по элементарной математике: Геометрия: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов и учителей. – М.: Просвещение, 1992.

Зеленяк О. П. Решение задач по планиметрии. Технология алгоритмического подхода на основе задач-теорем. Моделирование в среде Turbo Pascal. – Киев, Москва: ДиаСофтЮП, ДМК Пресс, 2008.

Шарыгин И. Ф. Геометрия. 7 – 9 кл.: Учеб. для общеобразоват. учеб. завед. – М.: Дрофа, 2001.

Шарыгин И.Ф. Решение задач: Учеб. пособие для 10 кл. общеобразоват. учреждений. – М.: Просвещение, 1994.

Шестаков С. А. Векторы на экзаменах. Векторный метод в стереометрии. – М.: МЦНМО, 2005.

🔥 Видео

ПОЧЕМУ СУММА УГЛОВ В ТРЕУГОЛЬНИКЕ РАВНА 180? #shorts #геометрия #егэ #огэ #треугольникСкачать

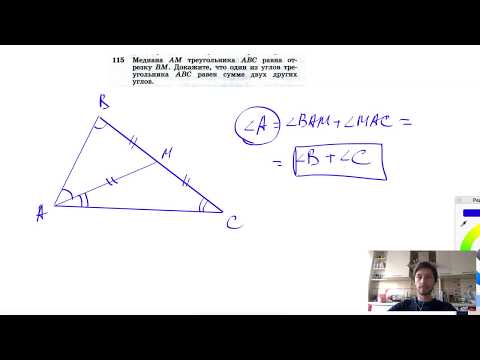
№115. Медиана AM треугольника ABC равна отрезку ВМ. Докажите, что один из углов треугольника ABCСкачать

Сумма углов треугольника равна 180Скачать

Задача про медиану треугольника и периметры. Геометрия 7 класс.Скачать

Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Формулы для медианы треугольникаСкачать

Найдите площадь треугольника, если его медианы равны 12, 15 и 21.Скачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Построение медианы в треугольникеСкачать

Длина медианы треугольникаСкачать

№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать