- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- Треугольник. Числовые зависимости между элементами треугольника (сторон, высот, медиан).
- Вычисление высоты треугольника по его сторонам.
- Вычисление медиан треугольника по его сторонам.
- Медиана треугольника
- 💡 Видео
Видео:8. Медиана треугольника и её свойства.Скачать

We are checking your browser. mathvox.ru
Видео:ОГЭ Задание 25 Свойство медиан прямоугольного треугольникаСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Формулы для медианы треугольникаСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Cloudflare Ray ID: 6d3574315e527b87 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:ЕГЭ задание 16 Длина медианыСкачать

Треугольник. Числовые зависимости между элементами треугольника (сторон, высот, медиан).
Теорема.
Если стороны прямоугольного треугольника измерены одной единицей, то квадрат числа, выражающего гипотенузу равен сумме квадратов чисел, выражающих катеты.
Эту теорему обыкновенно выражают сокращенно так:
Квадрат гипотенузы равен сумме квадратов катетов.
Это соотношение было впервые замечено греческим геометром Пифагором (VI в. до н.э.) и носит поэтому его имя — теорема Пифагора.
В треугольнике квадрат стороны, лежащей против острого угла, равен сумме квадратов двух других сторон без удвоенного произведения какой-нибудь из этих сторон на ее отрезок от вершины острого угла до высоты.
Пусть BС — сторона треугольника ABС (черт. 1 и черт. 2), лежащая против острого угла A , и BD — высота опущенная на какую-либо из остальных сторон, например, на AС (или на ее продолжение).Требуется доказать, что:
Из прямоугольных треугольников BDС и ABD выводим:
Подставив в равенство [1] вместо BD 2 и DС 2 их выражения из равенств [2] и [3] , получим:
Это равенство, после сокращения членов -AD 2 и +AD 2 , и есть то самое, которое требовалось доказать.
Замечание. Доказанная теорема остается верной и тогда, когда угол С прямой. Тогда отрезок СD обратится в ноль, т.е. AС станет равна AD, и мы будем иметь:
Что согласуется с теоремой о квадрате гипотенузы.
Теорема.
В треугольнике квадрат стороны, лежащей против тупого угла, равен сумме квадратов двух других сторон, сложенных с удвоенным произведением какой-нибудь из этих сторон на отрезок ее продолжения от вершины тупого угла до высоты. Доказательство аналогично предыдущему.
Следствие.
Из трех последних теорем выводим, что квадрат стороны треугольника равен, меньше или больше суммы квадратов других сторон, смотря по тому, будет ли противолежащий угол прямой, острый или тупой.
Отсюда следует обратное предложение: Угол треугольника окажется прямым, острым или тупым, смотря по тому, будет ли квадрат противолежащей стороны равен, меньше или больше суммы квадратов других сторон.
Видео:ЗАДАЧА О СУММЕ КВАДРАТОВСкачать

Вычисление высоты треугольника по его сторонам.
Обозначим высоту, опущенную на сторону а треугольника ABС , через ha. Чтобы вычислить ее, предварительно из уравнения:
находим отрезок основания с’:
.
После чего из DABD определяем высоту, как катет:
.
Таким же путем можно определить высоты hb и hс , опущенные на стороны b и с.
Видео:«СУММА КВАДРАТОВ» СУЩЕСТВУЕТ? | ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯСкачать

Вычисление медиан треугольника по его сторонам.
Пусть даны стороны треугольника ABС и требуется вычислить его медиану BD. Для этого продолжим ее на расстояние DE = BD и точку E соединим с A и С. Тогда получим параллелограмм ABCE.
Тогда .
Видео:Длина медианы треугольникаСкачать

Медиана треугольника
Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.
На рисунке 1 медианой является отрезок BD .
Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).
Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),
и заметим, что (см. раздел нашего справочника «Площадь треугольника»)
Поскольку отрезок BD является медианой, то
что и требовалось доказать.
Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.
Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).
Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).
Теперь рассмотрим четырёхугольник FEDG (рис. 5).
Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,
Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,
Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.
Следствие . Все три медианы треугольника пересекаются в одной точке.
Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).
Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.
Определение . Точку пересечения медиан треугольника называют центроидом треугольника.
Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).
Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна 
💡 Видео
Геометрия, 9 класс | Метод удвоения медиан.Скачать

Формула нахождения медианы треугольника по известным сторонам треугольника.Скачать

длина медианы #SHORTSСкачать
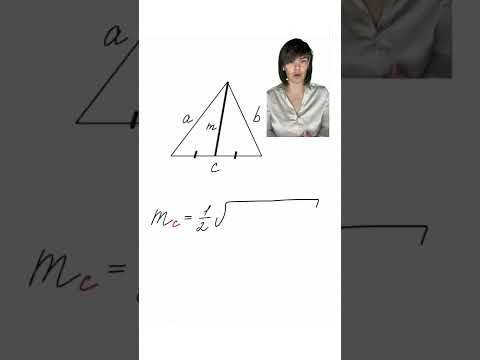
Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Сумма квадратов натуральных чисел через комбинаторику. Пример от wild mathing!Скачать

Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Кто краш и бро для медианы? Сериал про медианы 4 серияСкачать

Задача с региона — Сумма квадратовСкачать

🔥 Свойства МЕДИАНЫ #shortsСкачать

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Сумма квадратов диагоналей параллелограммаСкачать
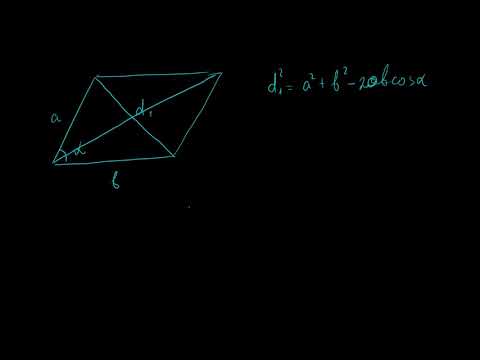
Сумма квадратов | Ботай со мной #061 | Борис Трушин |Скачать

Геометрия, ЕГЭ, часть 2. Задача 3. Все свойства медианы + формула для её нахожденияСкачать













