Градусная мера дуги окружности
Отметим на окружности две точки А и В. Они разделяют окружность на две дуги. Чтобы различать эти дуги, на каждой из них отмечают промежуточную точку, например L и М (рис. 214). Обозначают дуги так: 


Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности. На рисунке 215, а изображены две полуокружности, одна из которых выделена цветом.
Угол с вершиной в центре окружности называется её центральным углом. Пусть стороны центрального угла окружности с центром О пересекают её в точках А к В. Центральному углу АОВ соответствуют две дуги с концами А и В (рис. 215). Если ∠АОВ развёрнутый, то ему соответствуют две полуокружности (рис. 215, а). Если ∠АОВ неразвёрнутый, то говорят, что дуга АВ, расположенная внутри этого угла, меньше полуокружности. На рисунке 215, б эта дуга выделена цветом. Про другую дугу с концами А и В говорят, что она больше полуокружности (дуга ALB на рисунке 215, в).
Дугу окружности можно измерять в градусах. Если дуга А В окружности с центром О меньше полуокружности или является полуокружностью, то её градусная мера считается равной градусной мере центрального угла АОВ (см. рис. 215, а, б). Если же дуга АВ больше полуокружности, то её градусная мера считается равной 360° — ∠АОВ (см. рис. 215, в).
Отсюда следует, что сумма градусных мер двух дуг окружности с общими концами равна 360°.
Градусная мера дуги АВ (дуги ALB), как и сама дуга, обозначается символом 





Теорема о вписанном угле
Угол, вершина которого лежит на окружности, а стороны пересекают, окружность, называется вписанным углом.
На рисунке 217 угол АВС вписанный, дуга АМС расположена внутри этого угла. В таком случае говорят, что вписанный угол АВС опирается на дугу АМС. Докажем теорему о вписанном угле.
| Вписанный угол измеряется половиной дуги, на которую он опирается. |
Пусть ∠ABC — вписанный угол окружности с центром О, опирающийся на дугу АС (рис. 218). Докажем, что 
1) Луч ВО совпадает с одной из сторон угла АВС, например со стороной ВС (рис. 218, а). В этом случае дуга АС меньше полуокружности, поэтому ∠AOC = 
Отсюда следует, что
2∠1 = 
2) Луч ВО делит угол АВС на два угла. В этом случае луч ВО пересекает дугу АС в некоторой точке D (рис. 218, б). Точка D разделяет дугу АС на две дуги: 

Складывая эти равенства, получаем:
3) Луч ВО не делит угол ABC на два угла и не совпадает со стороной этого угла. Для этого случая, пользуясь рисунком 218, в, проведите доказательство самостоятельно.
| Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 219). |
| Вписанный угол, опирающийся на полуокруж ность, — прямой (рис. 220). |
Используя следствие 1, докажем теорему о произведении отрезков пересекающихся хорд.
| Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. |
Пусть хорды АВ и CD пересекаются в точке Е (рис. 221). Докажем, что
Рассмотрим треугольники ADE и СВЕ. В этих треугольниках углы 1 и 2 равны, так как они вписанные и опираются на одну и ту же дугу BD, а углы 3 и 4 равны как вертикальные. По первому признаку подобия треугольников ΔADE ∼ ΔCBE. Отсюда следует, что 
Задачи
649. Начертите окружность с центром О и отметьте на ней точку А. Постройте хорду АВ так, чтобы: a) ∠AOB = 60°; б) ∠AOB = 90°; в) ∠AOB = 120°; г) ∠AOB = 180°.
650. Радиус окружности с центром О равен 16. Найдите хорду АВ, если: a) ∠AOB = 60°; б) ∠AOB = 90°; в) ∠AOB =180°.
651. Хорды АВ и CD окружности с центром О равны.
а) Докажите, что две дуги с концами А и В соответственно равны двум дугам с концами С и D.
б) Найдите дуги с концами С и D, если ∠AOB = 112°.
652. На полуокружности АВ взяты точки С и D так, что 

653. Найдите вписанный угол АВС, если дуга АС, на которую он опирается, равна: а) 48°; б) 57°; в) 90°; г) 124°; д) 180°.
654. По данным рисунка 222 найдите х.
655. Центральный угол АОВ на 30° больше вписанного угла, опирающегося на дугу АВ. Найдите каждый из этих углов.
656. Хорда АВ стягивает дугу, равную 115°, а хорда АС — дугу в 43°. Найдите угол ВАС.
657. Точки А и В разделяют окружность на две дуги, меньшая из которых равна 140°, а большая точкой М делится в отношении 6 : 5, считая от точки А. Найдите угол ВАМ.
658. Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая AD, проходящая через центр О (D — точка на окружности, О лежит между А и D). Найдите ∠BAD и ∠ADB, если 
659. Докажите, что градусные меры дуг окружности, заключённых между параллельными хордами, равны.
660. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32°. Большая дуга окружности, заключённая между сторонами этого угла, равна 100°. Найдите меньшую дугу.
661. Найдите острый угол, образованный двумя секущими, проведёнными из точки, лежащей вне окружности, если дуги, заключённые между секущими, равны 140° и 52°.
662. Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если 

663. Отрезок АС — диаметр окружности, АВ — хорда, МА — касательная, угол МАВ острый. Докажите, что ∠MAB = ∠ACB.
664. Прямая AM — касательная к окружности, АВ — хорда этой окружности. Докажите, что угол МАВ измеряется половиной дуги АВ, расположенной внутри угла МАВ.
665. Вершины треугольника АВС лежат на окружности. Докажите, что если АВ — диаметр окружности, то ∠C > ∠A и ∠C > ∠B.
666. Хорды АВ и CD пересекаются в точке Е. Найдите ED, если:
а) АЕ = 5, ВЕ = 2, СЕ = 2,5; б) АЕ = 16, ВЕ = 9, CE = ED;
в) АЕ = 0,2, BE = 0,5, СЕ = 0,4.
667. Диаметр АА1 окружности перпендикулярен к хорде ВВ1 и пересекает её в точке С. Найдите ВВ1 если АС = 4 см, СА1 = 8 см.
668. Докажите, что перпендикуляр, проведённый из какой-нибудь точки окружности к диаметру, есть среднее пропорциональное для отрезков, на которые основание перпендикуляра делит диаметр.
669. Пользуясь утверждением, сформулированным в задаче 668, постройте отрезок, равный среднему пропорциональному для двух данных отрезков.
670. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекает окружность в точках Р и Q. Докажите, что АВ 2 = АР • AQ.
671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекает окружность в точках С и D. Найдите CD, если: а) АВ = 4 см, АС = 2 см; б) АВ = 5 см, AD = 10 см.
672. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекает окружность в точках В1 и С1, а другая — в точках В2 и С2. Докажите, что АВ1 • АС1 = АВ2 • АС2.
673. К данной окружности постройте касательную, проходящую через данную точку вне окружности.
Пусть даны окружность с центром О и точка А вне этой окружности. Допустим, что задача решена и АВ — искомая касательная (рис. 223). Так как прямая АВ перпендикулярна к радиусу ОВ, то решение задачи сводится к построению точки В окружности, для которой ∠ABO прямой. Эту точку можно построить следующим образом: проводим отрезок ОА и строим его середину О1. Затем проводим окружность с центром в точке Ох радиуса О1А. Эта окружность пересекает данную окружность в двух точках: В1В1. Прямые АВ и АВ1 — искомые касательные, так как АВ ⊥ ОВ и АВ1 ⊥ ОВ1. Действительно, углы АВО и АВ1O, вписанные в окружность с центром О1, опираются на полуокружности, поэтому они прямые. Очевидно, задача имеет два решения.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Центральные и вписанные углы
Тест по геометрии для 8 класса.
Вопрос №1
Полуокружность — это дуга с градусной мерой .
A) меньше 360 0
B) больше 180 0
C) 360 0
D) 180 0
Вопрос №2
Центральным углом называется .
A) угол 180 0
B) угол с вершиной в центре окружности
C) угол, проходящий через центр
D) угол, который находится в центре
Вопрос №3
Сумма градусных мер двух дуг окружности с общими концами равна
A) 90 0
B) 180 0
C) 270 0
D) 360 0
Вопрос №4
Вписанный угол — это .
A) угол, стороны которого опираются на окружность
B) угол, вершина которого лежит внутри окружности
C) угол, вершина которого лежит на окружности, а стороны пересекают окружность
D) угол, внутри которого вписана окружность
Вопрос №5
Вписанный угол измеряется .
A) градусной мерой дуги, на которую он опирается
B) половинной дуги, на которую он опирается
C) от 180 0 до 360 0
D) циркулем и транспортиром
Вопрос №6
Вписанный угол, опирающийся на полуокружность .
A) развернутый
B) прямой
C) тупой
D) острый
Вопрос №7
Вписанные углы, опирающиеся на одну и ту же дугу .
A) смежные
B) равные
C) односторонние
D) вертикальные
Вопрос №8
Если две хорды окружности пересекаются, то .
A) сумма отрезков одной хорды равна сумме отрезков другой хорды
B) сумма верхних отрезков равна сумме нижних отрезков
C) произведение отрезков одной хорды равно произведению отрезков другой хорды
D) произведение отрезков одной хорды равно среднеарифметическому отрезков другой хорды
Вопрос №9
Если центральный угол равен 460 , то вписанный угол, опирающийся на ту же дугу, равен
A) 46 0
B) 92 0
C) 23 0
D) 44 0
Вопрос №10
Если вписанный угол равен 116 0 , то центральный угол, опирающийся на ту же дугу, равен
A) 64 0
B) 116 0
C) 58 0
D) 232 0
Вопрос №11
Если вписанный угол равен 58 0 , то дуга на которую он опирается равна
A) 58 0
B) 116 0
C) 29 0
D) 32 0
Вопрос №12
Если вписанный угол лежит на диаметре, то он равен
A) 900
B) 180
C) 2700
D) 3600
Вопрос №13
Если центральный угол равен 134 0 , то дуга на которую он опирается равна
A) 268 0
B) 46 0
C) 134 0
D) 67 0
Видео:Градусная мера дуги окружности | Геометрия 7-9 класс #70 | ИнфоурокСкачать

Верно ли, что прямая, имеющая с окружностью одну общую точку, называется касательной?
Верно ли, что угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным?
Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности?
Верно ли, что если все вершины многоугольника лежат на окружности, то окружность называется описанной?
Верно ли, что дуга, концы которой соединяет отрезок, являющийся диаметром, называется полуокружностью?
Ошибочно ли, что каждая точка биссектрисы равноудалена от его сторон?
Верно ли, что касательная к окружности перпендикулярна к радиусу, проведённому в точку касания?
Верно ли, что вписанный угол измеряется половиной дуги, на которую он опирается?
Верно ли, что если многоугольник касается сторонами окружности, то он описанный?
Вписан ли четырехугольник?
Верно ли, что вершина центрального угла лежит на окружности?
Является ли верным то, что биссектрисы треугольника пересекаются в одной точке?
Верно ли, что если прямая проходит через конец радиуса, то она касательная?
Верно ли, что хорда АВ равна 16?
Верно ли, что в не каждый треугольник можно вписать окружность?
Верно ли, что около любого треугольника можно описать окружность?
Верно ли, что сумма градусных мер двух дуг окружности с общими концами рано 360 градусов?
Верно ли, что серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему?
Верно ли, что угол a равен b?
Верно ли, что x=68 градусов?
Верно ли, что AB+CD=BC+AD?
Верно ли, что в любом описанном четырехугольнике сумма противоположных углов равна 180 градусам?
Верно ли, что x=36 градусов?
Ошибочно ли, что каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка?
Верно ли, что если угол АОВ равен 60 градусам, а радиус ОВ равен 12, то касательная АВ равна 12 и корню из 3?
Верно ли, что x=205 градусов?
Верно ли, что в любой четырехугольник можно вписать окружность?
Верно ли, что радиус равен 10?
Верно ли, что a>b?
Истинно ли, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке?
Верно ли, что прямая p пересекает окружность, если радиус r=16, а d=12, где d – кратчайшее расстояние до p?
Верно ли, что AE*BE=CE*ED?
Верно ли, что в треугольник можно вписать больше одной окружности?
Верно ли, что радиус равен 18?
6. Превосходит ли хорда АВ радиус окружности, если радиус равен 13, а центральный угол АОВ 90 градусов?
Верно ли, что если угол AMB равен 136 градусов, то углы ACM и BCM равны 46 градусам?
| № Ответа | № Ответа | № Ответа | № Ответа | № Ответа | № Ответа | Число верных ответов |
| 1 | 7 | 13 | 19 | 25 | 31 | |
| 2 | 8 | 14 | 20 | 26 | 32 | |
| 3 | 9 | 15 | 21 | 27 | 33 | |
| 4 | 10 | 16 | 22 | 28 | 34 | |
| 5 | 11 | 17 | 23 | 29 | 35 | |
| 6 | 12 | 18 | 24 | 30 | 36 |
ПомощьПоле знаний.Далле ответьте на все вопросы, выбирая «да» или «нет». За каждый верный ответ вы зарабатываете 1 балл. Правила работы.Вам предлагается 36 вопросов Вы отвечаете двумя способами: ‘Да’ — если ответ утвердительный, Пишите намПрисылайте свои замечания и предложения на на электронную почту. Мы всегда рады ответить на все ваши вопросы. 🌟 Видео8 класс, 33 урок, Градусная мера дуги окружностиСкачать  Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать  72. Градусная мера дуги окружностиСкачать 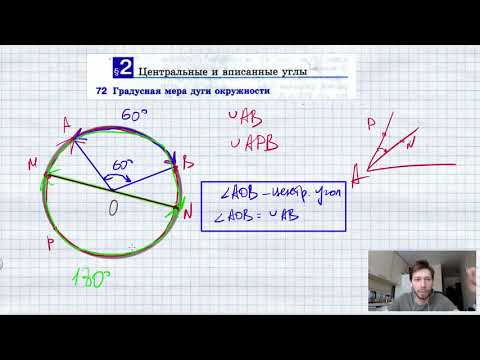 Длина дуги окружности. 9 класс.Скачать  Длина окружности. Математика 6 класс.Скачать  Геометрия 8 класс (Урок№26 - Градусная мера дуги окружности. Центральные углы.)Скачать  Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать  Центральный и вписанный углыСкачать  ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать  Решение задач на тему центральные и вписанные углы.Скачать  УГОЛ И ОКРУЖНОСТЬ: центральный угол, вписанный угол, длина дуги окружностиСкачать  Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать  Внешнее сопряжение дуги и прямой дугой заданного радиуса. Урок16.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать  Радиус и диаметрСкачать  ✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать  Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать  8 класс, 34 урок, Теорема о вписанном углеСкачать  ОГЭ 2023. Геометрия. Задача 16 "Центральные и вписанные углы"Скачать  |

























