Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке мы вспомним понятие биссектрисы угла, сформулируем и докажем прямую и обратную теоремы о свойствах биссектрисы, обобщим их. Решим задачу, в которой, кроме фактов о биссектрисе, применим другие геометрические факты.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Видео:Секретная формула биссектрисы треугольника плюс Задача из экзамена 9 классСкачать
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Видео:Формула для биссектрисы треугольникаСкачать
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Видео:Свойство биссектрисы треугольника с доказательствомСкачать
Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать
Формулы для вычисления длины биссектрисы треугольника
Формулы для вычисления длины биссектрисы треугольника
Можно вывести различные формулы, с помощью которых можно вычислить длину биссектрисы треугольника, если известны:
· длины прилежащих сторон и угол между ними
· длины прилежащих сторон и отрезки, на которые биссектриса разбивает противолежащую сторону
· длины трех сторон треугольника.
Докажем первую из формул.
Задача 1. Вычислить длину биссектрисы треугольника, если известны длинны двух прилежащих сторон треугольника и угол между ними.
Решение. Пусть в треугольнике АВС известно, что
.
Обозначим биссектрису AD через la .
.
Используя формулу синуса двойного угла, получаем:
.
Ответ: .
Выражение 
называется средним гармоническим чисел а и с. Поэтому формулу 
можно запомнить следующим образом:
биссектриса треугольника равна произведению среднего гармонического прилежащих сторон треугольника на косинус половинного угла между ними.
Доказательство остальных формул можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Задача 2. Вычислите биссектрису треугольника ABC, проведённую из вершины А, если ВС = 18, АС = 15, АВ = 12.
Решение. Воспользуемся формулой для вычисления биссектрисы угла, если известны три стороны треугольника: 
Задача 3. Определить площадь треугольника, если две его стороны равны 35 см и 14 см, а биссектриса угла между ними содержит 12 см.
Пусть в треугольнике АВС АС=35, АВ=14, AD — биссектриса, AD=12.
,
Вычислим 
, получаем:
, 
.
(по основному тригонометрическому тождеству).
Далее по формуле синуса двойного угла вычисляем
.
Для вычисления площади треугольника воспользуемся формулой 
.
Задача 4. . В равнобедренном треугольнике BCD с основанием BD
проведена биссектриса BE. Известно, что СЕ = 20 и DE = 10. Найдите BE.
Используя свойство биссектрисы угла треугольника (урок 4), получаем
, то есть 
.
Таким образом, нам известны длины двух прилежащих сторон и отрезки, на которые биссектриса разбивает противолежащую сторону, поэтому 
Ответ :
.
Задачи для самостоятельного решения
1. Дан треугольник со сторонами 4, 8, 9. Найти длину биссектрисы, проведенной к большей стороне.
2. В треугольнике ABC известно, что АВ = 10, АС = 15, 
BAC = 120°. Найдите биссектрису AD.
3. Катеты прямоугольного треугольника равны 6 и 8. Найдите биссектрису треугольника, проведённую из вершины прямого угла.
4. В равнобедренном треугольнике BCD с основанием BD проведена биссектриса BE. Известно, что СЕ = 18 и DE = 12. Найдите BE.
🔥 Видео
Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать
Построение биссектрисы угла. 7 класс.Скачать
Как решать задачу №16 ЕГЭ математика | Биссектрисы треугольникаСкачать
Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать
Cекретное свойство биссектрисыСкачать
Найдите биссектрису треугольникаСкачать
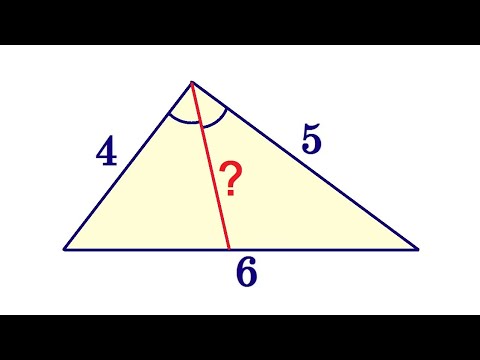
Как найти биссектрису в треугольнике? 2 формулы биссектрисыСкачать
Построение биссектрисы углаСкачать
7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать
Биссектрисы треугольника.Скачать
Решение задачи по теме "Свойство биссектрисы треугольника"Скачать
Задачи про медиану, биссектрису и высоту в треугольникеСкачать
Секретные формулы биссектрисы треугольника!😉❤️🔥#математика #егэСкачать
Периметр и биссектрисы треугольника (Задача №324622)Скачать
Построение биссектрисы в треугольникеСкачать
