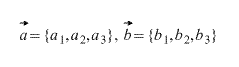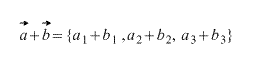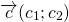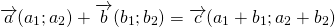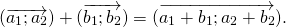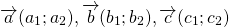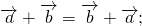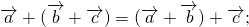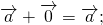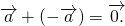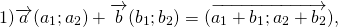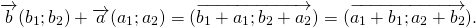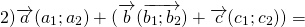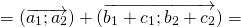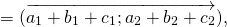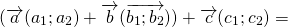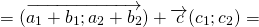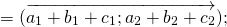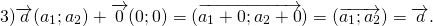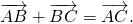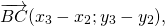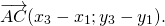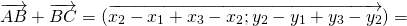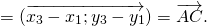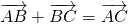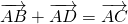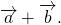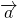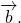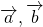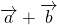Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .
Из данного выше построения сразу же будет следовать единственность данного вектора.
- Сумма векторов. Сложение векторов. Правило треугольника
- Разность векторов. Вычитание векторов
- Умножение вектора на число
- Геометрия сумма двух векторов
- Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.
- Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
- Покоординатное сложение векторов.
- Правило параллелограмма. Сложение векторов по правилу параллелограмма.
- Правило треугольника. Сложение векторов по правилу треугольника.
- Тригонометрический способ. Сложение векторов тригонометрическим способом.
- Сложение и вычитание векторов
- Сумма векторов. Сложение векторов. Правило треугольника
- Разность векторов. Вычитание векторов
- Умножение вектора на число
- Сумма и разность векторов
- Сумма векторов
- Формула сложения векторов
- Свойства сложения векторов
- Разность векторов
- Формула вычитания векторов
- Примеры задач
- Сложение векторов
- 💥 Видео
Видео:Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

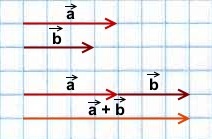
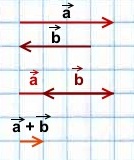
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора ( overrightarrow ) выполняется равенство
Для произвольных точек ( A, B и C ) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Видео:8 класс, 43 урок, Сумма двух векторовСкачать

Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )
Длина нулевого вектора равна нулю:
( left| vec right| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Умножение вектора на число
Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .
Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;
Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow=koverrightarrow ) .
Видео:82. Сложение двух векторовСкачать

Геометрия сумма двух векторов
Видео:Сумма двух векторов | Геометрия 7-9 класс #79 | ИнфоурокСкачать

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.
Видео:10 класс, 41 урок, Сумма нескольких векторовСкачать

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
- скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
- векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..
Рассмотрим сначала алгебраический подход к сложению векторов.
Покоординатное сложение векторов.
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов:
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
Правило параллелограмма. Сложение векторов по правилу параллелограмма.
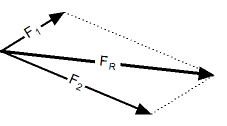
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
- нарисовать первый вектор, учитывая его величину и направление
- от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
- дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны
- результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.
 | Сложение векторов по правилу треугольника заключается в следующем:
|
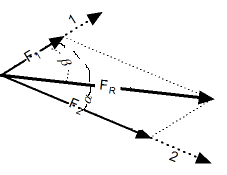 | Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:
Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:
|
Пример — сложение векторов.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Fрез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2
Угол между результирующей силой и первой силой равен:
А угол между второй и результирующей силой можно посчитать следующим образом: as
α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
Консультации и техническая
поддержка сайта: Zavarka Team
Видео:Сложение векторов. 9 класс.Скачать

Сложение и вычитание векторов
Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .
Из данного выше построения сразу же будет следовать единственность данного вектора.
Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( + , + , + > right) )
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора ( overrightarrow ) выполняется равенство
Для произвольных точек ( A, B и C ) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Видео:Сумма и разность векторов. Урок 2. Геометрия 9 классСкачать

Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )
Длина нулевого вектора равна нулю:
( left| vec right| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( — , — , — > right) )
Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Умножение вектора на число
Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .
Длина вектора ( overrightarrow ) равна ( left|overrightarrow right|=left|kright||overrightarrow| ) ;
Обозначение: ( overrightarrow =koverrightarrow ) .
Видео:Новое задание профиля №2. Все, что нужно знать о векторах | Аня МатеманяСкачать

Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Видео:Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

Сумма векторов
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
| Для плоских задач |
| Для трехмерных задач |
| Для n-мерных векторов |
Свойства сложения векторов
1. Коммутативность: a + b = b + a
2. Ассоциативность: ( a + b ) + c = a + ( b + c )
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (- a ) = 0
Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.
Видео:Вычитание векторов. 9 класс.Скачать

Разность векторов
Для вычитания векторов также применяется правило треугольника.
Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:
Формула вычитания векторов
Элементы вектора c равны попарной разности соответствующих элементов a и b .
| Для плоских задач |
| Для трехмерных задач |
| Для n-мерных векторов |
Видео:Сумма двух векторов. Правило треугольника. Законы сложения векторов. Правило параллелограмма.Скачать

Примеры задач
Задание 1
Вычислим сумму векторов и .
Задание 2
Найдем разность векторов и .
Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Сложение векторов
Сумма векторов
Свойства сложения векторов:
Для любых векторов
3) свойство прибавления нулевого вектора:
4) сумма противоположных векторов равна нулевому вектору:
Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:
Так как соответствующие координаты равны, то эти векторы равны.
(О сложении векторов)
Каковы бы ни были точки A, B, C, имеет место векторное равенство:
Что и требовалось доказать.
Правило треугольника построения суммы двух векторов
Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.
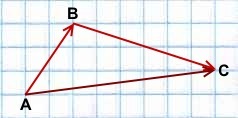
(то есть это правило следует из теоремы о сложении векторов).
Правило параллелограмма построения суммы двух векторов
Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.
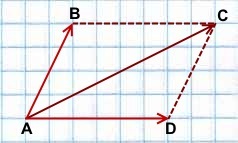
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.
При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.
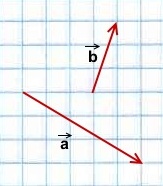
1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора
Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).
2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы
от общего начала.
Достроим на этих векторах параллелограмм.
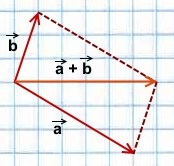
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.
1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.
2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.
Фактически в обоих случаях мы используем правило треугольника сложения векторов:
от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.
Из неравенства треугольника следует ещё два свойства сложения векторов:
💥 Видео
8 класс, 45 урок, Сумма нескольких векторовСкачать

2 урок. Сложение и вычитание векторов | Геометрия. 9 классСкачать

Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Сложение двух векторовСкачать

10 класс, 40 урок, Сложение и вычитание векторовСкачать