8.1. Фронтальные диметрические проекции окружностей. Если на аксонометрическом изображении хотят некоторые элементы. например окружности (рис. 64), сохранить неискаженными, то применяют фронтальную диметрическую проекцию. Построение фронтальной диметрической проекции детали с цилиндрическим отверстием, два вида которой даны на рисунке 64, а, выполняют так:
- Пользуясь осями х, у, z, строят тонкими линиями очертания внешней формы детали (рис. 64, б).
- Находят центр отверстия на передней грани. Через него параллельно оси у проводят ось отверстия и откладывают на ней половину толщины детали. Получают центр отверстия, расположенный на задней грани.
- Из полученных точек как из центров проводят окружности, диаметр которых равен диаметру отверстия (рис. 64, в).
- Удаляют лишние линии и обводят видимый контур детали (рис. 64, г).
Рис. 64. Построение фронтальной диметрической проекции
Постройте в рабочей тетради фронтальную диметрическую проекцию детали, изображенной на рисунке 64, а. Ось у направьте в другую сторону. Величину изображения увеличьте примерно в два раза.
8.2. Изометрические проекции окружностей. Изометрической проекцией окружности (рис. 65) является кривая, которая называется эллипсом. Эллипсы строить трудно. В практике черчения вместо них часто строят овалы. Овал — замкнутая кривая, очерченная дугами окружностей. Овал удобно строить, вписывая в ромб, который является изометрической проекцией квадрата.
Рис. 65. Изображение в изометрической проекции окружностей вписанных в куб
Построение овала, вписанного в ромб, выполняют в такой последовательности.
Вначале строят ромб со стороной, равной диаметру изображаемой окружности (рис. 66, а). Для этого через точку О проводят изометрические оси х и у. На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b, с и d проводят прямые, параллельные осям; получают ромб.
Рис. 66. Построение овала
Большая ось овала располагается на большой диагонали ромба.
После этого вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги. Их радиус R равен расстоянию от вершины тупого угла (точек А и В) до точек с, d или a, b соответственно (рис. 66, б).
Через точки В и а, В и b проводят прямые. В пересечении прямых Ва и ВЬ с большей диагональю ромба находят точки С и D (рис. 66, а). Эти точки будут центрами малых дуг. Их радиус R1 равен Са (или Db). Дугами этого радиуса плавно соединяют большие дуги овала.
Мы рассмотрели построение овала, лежащего в плоскости, перпендикулярной оси z (овал 1 на рисунке 65). Овалы, находящиеся в плоскостях, перпендикулярных оси у (овал 2) и оси х (овал 3), строят также. Только для овала 2 построение ведут на осях х и z (рис. 67, а), а для овала 3— на осях у и z (рис. 67, б). Рассмотрим, как применяются изученные построения на практике.
Рис. 67. Построение овалов: а лежащего в плоскости, перпендикулярной оси у; б — лежащего в плоскости, перпендикулярной оси x
Рис. 68. Построение изометрической проекции детали с цилиндрическим отверстием
8.3. Способ построения аксонометрических проекций предметов, имеющих круглые поверхности. На рисунке 68, а дана изометрическая проекция планки. Надо изобразить цилиндрическое отверстие, просверленное перпендикулярно передней грани. Построение выполняют так:
- Находят центр отверстия па передней грани. Определяют направление изометрических осей лля построения ромба (см. рис. 65). Из найденного центра проводят оси (рис. 68, а) и откладывают на них отрезки, равные радиусу окружности.
- Строят ромб. Проводят его большую диагональ (рис. 68, б).
- Описывают большие дуги. Находят центры для малых дуг (рис. 68. в).
- Проводят из найденных центров малые дуги.
Такой же овал строят на задней грани, но обводят лишь видимую его часть (рис. 68, г).
- На рисунке 69, а проведены оси для построения трех ромбов. Укажите, на какой грани куба — верхней, боковой правой, боковой левой (см. рис. 65) —будет расположен каждый ромб. Какой оси будет перпендикулярна плоскость каждого из этих ромбов? А какой оси перпендикулярна плоскость каждого из овалов (рис. 69, б)?
Рис. 69. Задание для упражнений
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Стороны ромбов равны 30 мм чему равны диаметры окружностей
МЕТОДИКА ПОИСКА МЕСТА ПОВРЕЖДЕНИЯ СИЛОВОГО КАБЕЛЯ
Типы повреждений и первоочередные мероприятия
При возникновении неисправности силового кабеля (обрыв, короткое замыкание, пробой изоляции), как правило, срабатывает защита, и кабель отключается от сети электроснабжения. Для выяснения причины неисправности необходимо провесги анализ причины отключения и тип повреждения.
Типы повреждения:
- однофазное замыкание на «землю»;
- межфазное КЗ;
- двухфазное КЗ на «землю»;
- обрыв жилы кабеля.
Рассмотрим последовательность поиска места повреждения с использованием описанных выше приборов. Для поиска места повреждения кабеля необходимо подготовить рабочее место: отключить и отсоединить кабель с двух сторон, а также проверить по схеме, что нет никаких транзитных ответвлений.
После выполнения организационно — технических мероприятий необходимо провести измерение сопротивления изоляции между фазами и между фазами и «землей» и провести анализ состояния сопротивления изоляции кабеля. По состоянию сопротивления изоляции кабеля можно сделать вывод о типе повреждения.
Подсоединив рефлектометр (Р-5-10, Р-5-13 или другой) к жилам кабеля, просмотреть эгпоры по фазам и определить предварительное расстояние до места повреждения.
Если повреждение однофазное КЗ или переходное сопротивление большое, то кабель необходимо «дожечь». Для этого используются установки прожига (дожита) кабеля типа: УП-7, АПК-14, МПУ-З «Феникс» и т. д.
После предварительного определения места повреждения кабеля проводится поиск точного места повреждения. Для точной локализации места повреждения используются поисковые комплекты «Успех АТГ-209».
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Радиус и диаметр окружности
Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).
Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.
Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности
Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.
Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.
На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;
Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.
Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.
Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.
Формула радиуса окружности через диаметр:
Формула диаметра окружности через радиус:
Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.
Существует радиус вписанной окружности
и радиус описанной окружности.
Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.
Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.
Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.
🎬 Видео
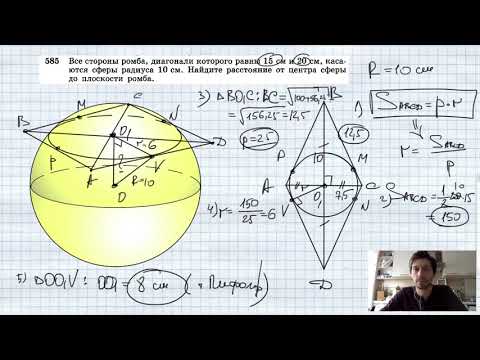
№585. Все стороны ромба, диагонали которого равны 15 см и 20 см, касаются сферы радиуса 10 см. НайдиСкачать
№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

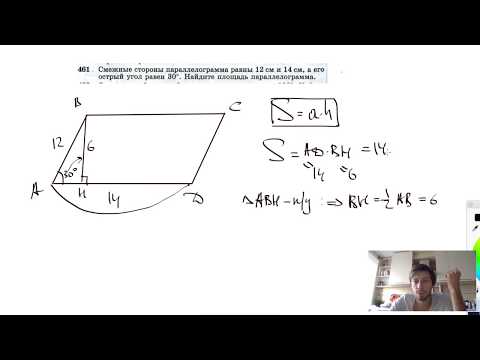
№461. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. НайдитеСкачать
Длина окружности. Площадь круга - математика 6 классСкачать

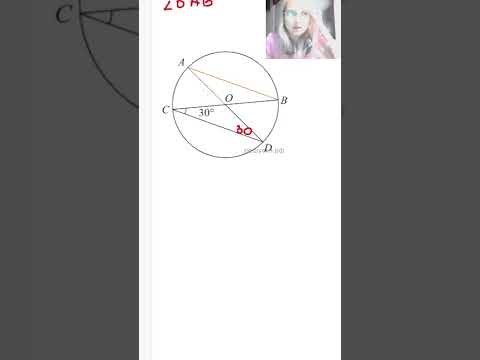
В окружности проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.Скачать
№493. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.Скачать

Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

2017 на окружности по разные стороны от диаметра AB взяты Точки M и NСкачать

Геометрия Один из углов ромба равен 60, а большая диагональ равна 24 см. Найдите радиус окружностиСкачать

ОГЭ 2024. Математика. Вариант 19. 50 вариантов. Под ред. И.В. Ященко. Задания 1 - 19Скачать

Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

Шины ОГЭ 2023. Задания 1-5 ОГЭ по математикеСкачать

Ромб. Свойства ромба. Решение задач.Скачать

ОГЭ по математике 2024 разбор 17 варианта Ященко и ФИПИ / ПДФ решение + формулы / МатТаймСкачать








