Степень точки — относительно окружности радиуса r называется величина:
(d — расстояние от точки до центра окружности, r — радиус окружности) Степень внешней точки — положительная, степень внутренней точки — отрицательная. Для точек окружности степень точки равна нулю.
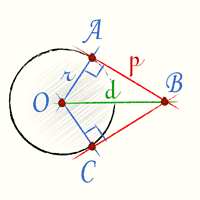 степень внешней точки | 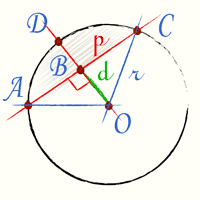 степень внутренней точки |
Абсолютная величина степени точки обозначается так:
Если точка B — внешняя, то абсолютная величина степени точки есть квадрат длины касательной AB.
Если точка B — внутренняя, то степень точки равна квадрату наименьшей полухорды, проходящей через эту точку.
Видео:✓ Степень точки в ЕГЭ | Резерв досрока ЕГЭ-2022. Задание 16. Профильный уровень | Борис ТрушинСкачать
Зачем нужна степень точки? Практические задачи.
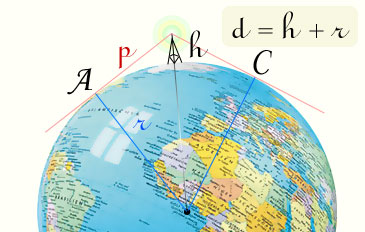
Практической задачей, где используется степень точки является например вычисление дальности вещания УКВ радиостанций. Известно, что радиоволны УКВ диапазона распространяются прямолинейно, как свет и прием возможен только в зоне прямой видимости. Таким образом зная высоту антенны и радиус Земли, вычислим степень точки и получим дальность вещания. Взяв средний радиус Земли 6350 километров, высота антенны например 200 метров — после расчета получим дальность связи (степень точки) ≈ 50.4 километров.
Видео:Степень точки и радикальные оси | Олимпиадная математикаСкачать
Радикальная ось.
Определение. Радикальная ось двух не концентрических окружностей — геометрическое место точек, имеющих равные степени относительно этих окружностей.
Теорема. Если две окружности не концентрические, то их радикальная ось существует и является прямой, перпендикулярной линии, проходящей через центры этих окружностей.
Утверждение 1. Если степени точки относительно двух окружностей равны, то равны отрезки касательных, проведенные из нее к этим окружностям.
Утверждение 2. Если к двум окружностям проведены две внешние и две внутренние касательные, то середины отрезков, соединяющих точки касания, лежат на одной прямой.
Утверждение 3. Общая касательная двух окружностей делится их радикальной осью пополам.
Утверждение 4. Радикальная ось двух пересекающихся окружностей проходит через точки их пересечения.
Утверждение 5. Радикальная ось двух касающихся окружностей есть их общая касательная, проведённая в точке касания.
Утверждение 6. Радикальная ось двух непересекающихся окружностей не пересекает ни одну из них.
Теорема. Три прямые, являющиеся радикальными осями пар трех не концентрических окружностей пересекаются в одной точке или параллельны или совпадают. Если центры окружностей лежат на одной прямой, то их радикальные оси перпендикулярны этой прямой, то есть параллельны или совпадают. Если центры окружностей не лежат на одной прямой, то их радикальные оси пересекаются в одной точке.
Определение. Для трех окружностей, центры которых не лежат на одной прямой, точка, для которой ее степени относительно всех трех окружностей равны, называется радикальным центром трех окружностей.
Видео:Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 1Скачать
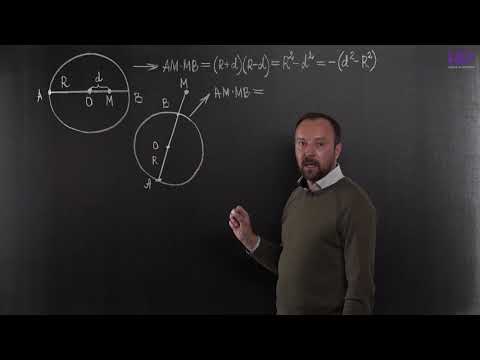
Степень точки относительно двух окружностей
Аполлоний Пергский (ок. 262–170 до н. э.) завоевал среди современников титул Великого Геометра. Он обучался в Александрии у последователей Евклида, имена которых не сохранились, и стал последним великим представителем александрийской математической школы. Позднее он работал в Пергаме, где создал свой важнейший труд «Коноика» («Конические сечения»), который и принес ему такую громкую славу. Только первые четыре книги этого произведения дошли до нас в подлиннике. Три другие сохранились в арабском переводе, а восьмая, последняя, была утрачена. Работа Аполлония оказала огромное влияние на развитие не только математики, но и астрономии, механики, оптики. Именно он ввел в язык математики названия «эллипс», «парабола», «гипербола», «фокус», «асимптота».
Благодаря позднейшим комментаторам и реставрациям, которыми много занимались в 16-18 вв., мы знаем и о содержании шести других геометрических работ Аполлония. В одной из них появляется так называемая «окружность Аполлония». В другой, изданной Виетом, работе «О касании» рассматривается следующая задача: построить циркулем и линейкой окружность, касающуюся трех данных окружностей. Решение самого Аполлония не сохранилось, но предпринятые многими авторами попытки его восстановления и, конечно, привлекательная формулировка, сделали эту задачу очень популярной. Мы предлагаем серию чертежей-заданий, которые через череду вспомогательных задач приводят к одному из элементарных, «школьных» решений.
Частные случаи
Нам будет удобно несколько расширить рамки задачи и допустить, наряду с обычными окружностями, «вырожденные» – точки (окружности нулевого радиуса) и прямые (окружности бесконечного радиуса). При этом появится несколько частных случаев, определяемых тем, какие именно фигуры (точки, прямые и окружности) даны, но, как мы увидим, к этим более простым случаям будет сводиться общий. Сначала посмотрим, как решается задача, когда все три данные окружности вырождаются в точки и прямые.
Три точки (Задача 01, 02). В этом случае задача состоит в том, чтобы описать окружность около треугольника с вершинами в трех данных точках. Этому учат едва ли не на первых уроках геометрии. Отметим, что и в случае, когда даны точки на одной прямой, эта задача имеет решение, ведь мы условились и прямую считать окружностью.
Три прямые (Задача 03, 04). В отличие от первого случая, здесь возможны несколько решений. Если прямые ограничивают треугольник, то одно из них дается его вписанной окружностью, а еще три – вневписанными (касающимися одной из сторон извне треугольника и продолжений двух других сторон). Если параллельны ровно две из трех прямых, то решений, очевидно, два, а если все три, то ни одного.
Две точки и прямая (Задача 05). Эту задачу можно решить с помощью «геометрических вычислений», т. е. алгебраическим методом. Пусть A и B – данные точки и пусть C – точка пересечения прямой AB с данной прямой l (случай AB || l рассмотрите самостоятельно). Если K – точка касания искомой окружности с прямой l, то по теореме о квадрате касательной должно выполняться равенство CK 2 = CA·CB. Это позволяет построить точку K, отложив на прямой l отрезок CK длины
| _____ |
| CK = √CA·CB |
Две прямые и точка (Задача 07). Допустим, что данные прямые пересекаются. Тогда задачу можно свести к предыдущей. Поскольку центр окружности, касающейся таких прямых, лежит на биссектрисе l одного из образованных ими углов, окружность симметрична относительно l, поэтому она проходит через точку B, симметричную данной точке A относительно l. Таким образом, нам известны две точки, A и B, лежащие на искомой окружности, и две прямые, которых она касается, а построение для этого случая (даже для одной прямой) было описано выше. Для полноты надо отдельно рассмотреть случаи, когда прямые параллельны и когда они пересекаются, но данная точка лежит на биссектрисе образованного ими угла (и совпадает с симметричной ей точкой B). Построение в этих случаях несложно и мы на нем не останавливаемся.
Последнюю задачу можно решать и непосредственно, методом гомотетии. В таком случае к ней можно было бы сводить предыдущую задачу о проведении окружности через две данные точки A и B, касающуюся данной прямой: искомая окружность обязана касаться и второй прямой, симметричной данной относительно серединного перпендикуляра к AB.
Прежде, чем двинуться дальше, остановимся на понятии степени точки относительно окружности и некоторых связанных с ним фактах, которые понадобятся нам еще не раз. Хотя это понятие в явном виде и не проходится в школе, по существу оно появляется в двух известных теоремах об окружности: теореме об отрезках пересекающихся хорд и теореме о квадрате касательной (ее другое название – теорема о секущей и касательной), которую мы уже использовали выше. Эти две теоремы можно свести в одно утверждение.
Пусть даны окружность и точка P. Произведение PA·PB, где A и B – точки, в которых прямая, проходящая через P, пересекает окружность, зависит только от точки P и окружности и не зависит от прямой.
Это произведение, взятое со знаком плюс для точек вне окружности и со знаком минус для точек внутри окружности, и называется степенью точки P относительно окружности. Можно сказать, что степень точки P – это скалярное произведение 
(равное в данном случае PA·PB, если векторы 
и 
сонаправлены и –PA·PB, если они противоположно направлены). Если точка P лежит вне окружности, то степень равна квадрату отрезка PK касательной, проведенной из точки P к окружности (это и есть теорема о квадрате касательной). Приведенные выше утверждения, объединяющие две школьные теоремы, будем называть теоремой о степени точки (относительно окружности).
Из нее нетрудно вывести и теорему, в некотором смысле к ней обратную: если прямые AB и CD пересекаются в точке P и 
, то точки A, B, C и D лежат на одной окружности, а если P лежит на прямой AB и PA·PB = PK 2 , то прямая касается окружности, проходящей через A, B и K.
Вернемся к задаче Аполлония и рассмотрим случаи, когда две окружности вырождены, т. е. являются точками или прямыми, а третья – «нормальная».
Две точки и окружность (Задача 06). Пусть требуется построить окружность, проходящую через данные точки A и B и касающуюся данной окружности c0. Проведем через A и B произвольную окружность c’, пересекающую c0 в точках C и D, и обозначим через P точку пересечения прямых AB и CD. Далее проведем через P касательную к данной окружности и обозначим через X точку касания. Тогда окружность c, проходящая через A, B и X, будет искомой. Действительно, степень точки P относительно c0 равна PX 2 = PC·PD. Применяя теорему о степени к окружности c’ и двум ее секущим PCD и PAB, находим, что PC·PD = PA·PB. Отсюда следует, что PX 2 = PA·PB, а значит прямая PX касается и окружности c, т. е. является общей касательной окружностей c0 и c. Следовательно, c касается c0 (в точке X). Из точки P можно провести две касательных к c0 и они дадут два решения нашей задачи. Можно показать, что других решений нет.
Наше решение не работает, если прямые AB и CD окажутся параллельными. Это произойдет, если серединный перпендикуляр к AB содержит центр данной окружности. Легко понять, что в этом случае точками касания будут точки пересечения серединного перпендикуляра с окружностью.
Две прямые и окружность (Задача 12). Если прямые параллельны, то радиус искомой окружности равен половине расстояния между ними, и ее центр легко строится. Допустим, что данные прямые a и b пересекаются в точке P, и обозначим через K неизвестную точку касания данной окружности c0 и искомой окружности c. Окружность c переходит в c0 при некоторой гомотетии с центром K. Эта гомотетия переводит прямую a, касающуюся c, в параллельную ей прямую a0, которая будет касаться c0. Прямую a0 легко построить. Так же строится и образ b0 прямой b при рассматриваемой гомотетии. А точка Q пересечения a0 и b0 – это образ точки P при той же гомотетии. Но любая точка, ее образ при гомотетии и центр гомотетии лежит на одной прямой. Значит, точка K лежит на пересечении прямой PQ с данной окружностью. Теперь задача свелась к построению окружности, касающейся данных прямых и проходящей через данную точку K, а это мы уже делали выше. Поскольку каждую из касательных a0 и b0 можно провести двумя способами, а прямая PQ может иметь до двух точек пересечения с данной окружностью, задача может иметь до восьми решений (по два в каждом из углов, образованных данными прямыми), но может быть и меньше.
Сделаем очередную остановку и обратим внимание на примененное в этом решении преобразование гомотетии. Не только касающиеся, но и любые две окружности гомотетичны друг другу, причем двумя способами, если только они не равны. Чтобы построить центры двух гомотетий – центры подобия окружностей – проведем в окружностях параллельные радиусы и соединим прямыми их концы. Точки пересечения этих прямых с линией центров и будут центрами подобия. При этом прямая, соединяющая концы радиусов, лежащих по одну сторону от линии центров, дает центр гомотетии с положительным коэффициентом, равным отношению радиусов, а для второй прямой получается коэффициент, равный тому же числу со знаком минус. В первом центре подобия пересекаются внешние касательные к окружностям и его так и называют внешним, а во втором, внутреннем, – внутренние касательные (конечно, если соответствующие касательные существуют). Построив эти центры, мы построим и касательные. (Заметим, кстати, что проведение касательной к двум окружностям тоже можно рассматривать как частный случай задачи Аполлония, в котором две из данных окружностей – прямые, а третья – бесконечно-удаленная точка, из-за чего искомая окружность сама превращается в прямую.) Если две окружности равны, то «отрицательная» гомотетия превращается в центральную симметрию, а «положительная» – в параллельный перенос.
Теперь можно продолжить рассмотрение различных вариантов задачи Аполлония.
Точка, прямая, окружность (Задача 08). Мы приведем построение, в котором соединяются идеи двух предыдущих – степень точки и гомотетия. Пусть A, a, c0 – данные точка, прямая и окружность, c – искомая окружность, K и L – точки ее касания с c0 и a, соответственно. При гомотетии с центром K, переводящей c в c0, прямая a перейдет в параллельную ей касательную к c0. Поэтому точка L перейдет в такую точку M окружности c0, что выходящий из нее диаметр перпендикулярен к a. Обозначим второй конец этого диаметра через B, а точку, в которой он при продолжении пересекает a, через C. Пусть X – точка пересечения прямой AM с окружностью c. Точки B, C, L и K лежат на некоторой окружности, так как угол BCL = 90° и угол BKL = BKM = 90°. Поэтому MC·MB = MK·ML. Точки X, A, L и K лежат на одной окружности по построению, так что MK·ML = MX·MA. Поэтому точку X можно построить из соотношения MX·MA = MC·MB, в котором нам уже известны все точки, кроме X. Проще всего это сделать, проведя еще одну окружность – через A, B и C; X – это точка ее пересечения с MA. Теперь остается провести окружность, касающуюся a, через две известные точки A и X, а эту задачу мы уже умеем решать. Поскольку она имеет, вообще говоря, два решения, а в качестве точки M в нашем построении можно взять любой из двух концов диаметра (т. е. поменять точки M и B на рисунке ролями), наибольшее число решений в данном случае равно четырем.
Наконец, рассмотрим случаи, когда вырождается только одна окружность.
Точка и две окружности (Задача 09. 2). Пусть требуется построить окружность, проходящую через данную точку A и касающуюся двух данных окружностей c1 и c2 внешним образом. Пусть K1 и K2 – точки касания. Воспользуемся тем, что они лежат на одной прямой с внешним центром подобия Z данных окружностей. (Доказать это можно с помощью теоремы Менелая для треугольника OO1O2, образованного центрами окружностей: очевидно, что 
, где R1, R2 и R – радиусы соответствующих окружностей; равенство последних множителей в произведениях следует из того, что Z – центр гомотетии с коэффициентом R2: R1, переводящей O1 в O2.) По теореме о степени точки отсюда следует, что искомая окружность проходит через такую точку X прямой ZA, что ZX·ZA = ZK1·ZK2. Если мы найдем произведение в правой части этого равенства, то найдем и точку X, и тогда задача сведется к построению окружности, проходящей через две известные точки и касающейся известной окружности (любой из двух данных).
Отсюда вытекает следующее построение: проводим произвольную секущую ZL1L2, затем окружность через точки L1, L2 и A и находим X как точку пересечения этой окружности с прямой ZA, отличную от A. В итоге задача сводится к случаю, когда даны две точки (A и X) и окружность. В этом случае, как мы видели, имеется, вообще говоря, два решения. Одно из них – это окружность, касающаяся обеих данных внешним образом, второе – окружность, касающаяся обеих данных внутренним образом. Если выполнить аналогичное построение, взяв вместо внешнего центра подобия внутренний, мы получим еще два решения (c разноименным касанием).
Прямая и две окружности . Допустим, что мы построили окружность c, касающуюся данных окружностей внешним образом и прямой. Увеличим радиус построенной окружности на величину, равную радиусу r меньшей из данных окружностей. Тогда, очевидно, она пройдет через центр меньшей окружности и будет касаться «сжатой» на величину r второй данной окружности, а также прямой, полученной из данной параллельным сдвигом на ту же величину. Мы видим, что для расширенной указанным образом окружности c известны точка, через которую она проходит, а также окружность и прямая, которых она касается. А такую задачу мы уже решили выше. Окончательное решение получается сжатием на r построенной расширенной окружности. Другие решения можно получить аналогично с учетом различных случаев расположения окружностей. Например, чтобы построить окружность, которая касается обеих данных внутренним образом, нужно мысленно уменьшить ее радиус и радиусы данных окружностей на r и придвинуть прямую на ту же величину. Новая окружность пройдет через центр меньшей из данных, а касание со второй окружностью и прямой сохранится. Возможно до восьми решений.
Преобразование окружностей, которое мы здесь применили, так и называется расширением (фактически оно может оказаться и «сжатием»). Чтобы описать его, не рассматривая многочисленные частные случаи, зададим на окружностях и прямых направления, т. е., попросту говоря, нарисуем на них стрелки. При этом из каждой обычной окружности получатся две противоположно направленные. Две направленные окружности или окружность и прямую будем считать касающимися, если они имеют не только единственную общую точку, но и одинаковые направления в этой точке. Радиусу окружности припишем знак – плюс, если она ориентирована против часовой стрелки, и минус, если наоборот. При таком соглашении расширение окружности на величину l – это просто добавление l к радиусу (с учетом знаков), а для прямой – это сдвиг на |l| вправо от направления прямой при l>0 и влево при l 3 = 8 способами – и придерживаться сделанного выбора. Проследив всю цепочку построений, можно убедиться, что для каждого из этих способов имеется не более одной окружности заданной ориентации, касающейся трех данных «правильно», с соблюдением направлений. Поскольку ориентацию искомой окружности можно считать заданной раз и навсегда, скажем, против часовой стрелки, задача имеет не более восьми решений. Конечно, в каких-то случаях их может быть меньше.
Мы рассказали об «элементарном» решении задачи Аполлония, практически не использующем понятий, выходящих за рамки школьной программы. Существует и много других способов ее решения, из которых мы упомянем лишь об одном, с помощью удивительного преобразования плоскости, называемого инверсией.
Это преобразование как бы «выворачивает плоскость наизнанку», меняя местами внутренность и внешность некоторой окружности c. Его самое главное свойство состоит в том, что оно превращает окружности, проходящие через центр O окружности c в прямые и обратно, а окружности, не проходящие через центр, оставляет окружностями. Благодаря этому, фигуру из прямых и окружностей можно с помощью инверсии изменить самым радикальным образом. Например, если поместить центр O инверсии в точку пересечения двух окружностей, то она переведет их в пересекающиеся прямые, а любые две непересекающиеся окружности можно подходящей инверсией сделать концентрическими. Это значит, что задача Аполлония для любых трех окружностей сводится инверсией к случаю «две прямые и окружность», разобранному выше или к случаю, когда две данные окружности имеют общий центр, а значит диаметр искомой окружности известен – он равен ширине образованного ими кольца. Если же использовать инверсию в сочетании с расширением, то решение можно свести к совсем простым случаям. Например, с помощью расширения можно сделать какие-либо две из данных окружностей касающимися, тогда инверсия относительно точки касания переведет их в параллельные прямые. Можно также сжать одну из окружностей в точку, тогда инверсия относительно этой точки превратит искомую окружность в прямую и задача сведется к проведению общей касательной к образам двух других окружностей.
🎥 Видео
Задачи региона ВсОШ на степень точкиСкачать
Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 2Скачать
Степень точки, радикальная ось. Планиметрия из ВСОШ и Высшей пробы. Чтобы решать планиметрию нужно..Скачать
Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 3Скачать
Радикальные оси для ЕГЭ профиль. Геометрические конструкции, убивающие №16Скачать
9 класс, 8 урок, Взаимное расположение двух окружностейСкачать
Математика. ПЕРЕЧНЕВЫЕ ОЛИМПИАДЫ. Степень точки. Радикальные осиСкачать
Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 4Скачать
04 71196 Степень точкиСкачать
Пересечение двух окружностейСкачать
Геометрия на ЕГЭ. Расстояние от центра окружности до произвольной точки хорды. Степень точки.Скачать
Признаки подобия. Степень точки относительно окружности.Скачать
#1 Степень точки и радикальные оси - секретный приём из геометрии!Скачать
1 2 4 сопряжение окружностейСкачать
Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Степень точки, радикальная ось и центр и их применение (часть 2) | Курсы повышения квалификацииСкачать
Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать
