St средняя линия треугольника bmc (3 видео)

Геометрия. 10 класс

Содержание

Урок-практикум по теме «Взаимное расположение прямых в пространстве. Угол между двумя прямыми». 10-й класс
Дано: ST – средняя линия
Окружность
📽️ Видео

Расположение прямых в пространстве

Распределите рисунки по встречающимся в них типам расположения прямых

Некоторые подходят под несколько категорий, определите, с какими категориями соотносятся оставшиеся

Параллельно	Пересекаются	Скрещиваются

Расположение прямых в пространстве

Продолжите фразы, чтобы получилось верное высказывание:

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только
Если стороны двух углов соответсвенно , то такие углы равны.
Прямые, которые не лежат в одной плоскости называются

Угол между скрещивающимися прямыми

$ABCDA_B_C_D_$ – куб. Найдите угол между прямыми, содержащими отрезки AC и B₁D₁. Заполните пропуски в решении.

Прямая параллельна прямой B₁D₁ тогда угол между и B₁D₁ равен углу между и , но и – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно, ответ – 90°.

Расположение прямых в пространстве

Выберите верные утверждения:

Любые две пересекающиеся прямые лежат в одной плоскости и образуют четыре неразвернутых угла.

Параллельные прямые – это прямые, которые не пересекаются.

Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой

Скрещивающиеся прямые – это прямые, которые не пересекаются.

Расположение прямых в пространстве

Любая прямая рассекает плоскость на две полуплоскости. Если лучи параллельны и лежат в одной полуплоскости, то они называются:

Угол между скрещивающимися прямыми

Заполнив пропуски, Вы сможете разгадать кроссворд:

Прямые ОB и CD параллельные, а АО и CD – скрещивающиеся прямые. Найдите угол между прямыми АО и CD, если $angle$ АОВ = 135°.

$angle АОВ_$ = 180° – (1)____°, где В1 лежит по другую сторону от точки О, чем точка В

$angle АОВ_$ = (2)____°,

значит, именно угол $angle АОВ_$, есть угол между прямыми АО и CD.

Ответ: $angle АОВ_$ = (3)____°.

Расположение прямых в пространстве

Подчеркните верные высказывания о расположении прямых:

Две прямые в пространстве называются параллельными, если они не пересекаются.
Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо так же ей параллельна, либо лежит в этой плоскости.
Существует такая прямая, которая лежит в плоскости и параллельна прямой, пересекающей данную плоскость.
Скрещивающиеся прямые не имеют общих точек.

Прямая и плоскость

Постройте плоскость α, проходящую через точку К и параллельную скрещивающимся прямым а и b.

Построение: (укажите порядковый номер ответа)

Вставьте пропуски в тексте

Поставьте напротив вопроса номер ответа:

1 – не скрещивающиеся

3 – лежат в одной плоскости

Расположение прямых в пространстве

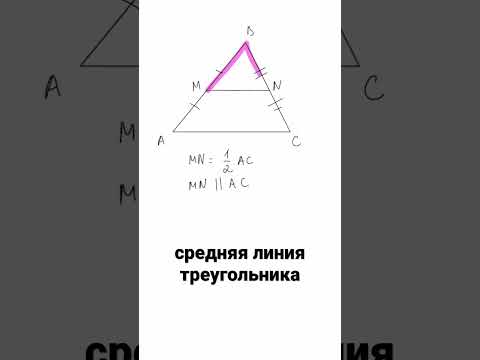
ST – средняя линия треугольника BMC.

PQ – средняя линия треугольника AMD.

XY – средняя линия трапеции ABCD.

Найдите PQ и ST, если XY = 15 см, BC : AD = 1 : 4.

Скрещивающиеся прямые

Дан куб ABCDA₁B₁C₁D₁. Укажите (в алфавитном порядке) номера пяти прямых, проходящих через точку В₁ и скрещивающихся с прямой А₁D.

Угол между скрещивающимися прямыми

Длина ребра правильного тетраэдра ABCD равна 1. Найдите угол между прямыми DM и CL, где M — середина ребра BC, L — середина ребра AB.

Поставьте напротив номера вопроса номер варианта ответа:

1. Пусть MF прямая, параллельная прямой ___ 2. и ___ точка её пересечения с AB.

3. Тогда искомый угол между прямыми DM и CL равен углу___.

4. Обозначим угол ____ буквой α.

5. MF — средняя линия треугольника BCL, поэтому:

Выразим квадрат отрезка DF по теореме косинусов в двух треугольниках: DMF и BDF.

= $BD^2 + BF^2-2BD · BF · cos60º$

Поскольку $DM=frac<sqrt>$ и BD = 1, подставляя числовые данные, получим:

$=1+frac-2cdot fraccdotfrac$ Получаем, что cosα=__. 8. Ответ: arccos =__.

Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

Урок-практикум по теме «Взаимное расположение прямых в пространстве. Угол между двумя прямыми». 10-й класс

Класс: 10

Учебная цель урока: научить учащихся решать задачи по пройденной теме.

Задачи урока:

обобщить и систематизировать теоретические сведения пройденной темы;
отработать умения учащихся по решению задач пройденной темы;
развивать пространственное мышление учащихся;
активизировать внимание учащихся с помощью применения мультимедийных средств;
прививать интерес к предмету.

Оборудование: компьютер, проектор.

Ход урока

1. Организационный момент.

Сообщение учащимся темы и определение цели урока. (Слайды 1, 2, 3)

2. Актуализация знаний.

Провести на листочках теоретический диктант с последующей взаимопроверкой. (Слайд 4)

3. Решение задач. (Приложение 1)

(Один ученик отвечает у доски, остальные – фиксируют решение в тетради.)

а) Прямые АВ₁ и СС₁ – скрещивающиеся. ∠(АВ₁; СС₁) = ∠(АВ₁; ВВ₁) = 45˚ (по свойству диагоналей квадрата).

б) Прямые АВ₁ и СD₁ – скрещивающиеся. ∠(АВ₁;СD₁) = ∠(АВ₁; ВА₁) = 90˚ (по свойству диагоналей квадрата).

Каково взаимное расположение прямых?
Как доказать, что прямые скрещивающиеся?
Какой угол называется углом между скрещивающимися прямыми?
Какую прямую, параллельную к одной прямой и пересекающую вторую прямую, можно рассмотреть?
Какими свойствами обладает фигура, содержащая отрезки выбранных нами пересекающихся прямых?

№43. (учебник стр. 19) (Слайд 8)

Какой четырехугольник называют пространственным?
Как изобразить пространственный четырехугольник?
Как на рисунке показать, что точка является серединой стороны?

Учащиеся самостоятельно записывают «дано» и «доказать».

Один ученик устно доказывает, что KLMN – параллелограмм, после чего учащиеся самостоятельно фиксируют доказательство в тетради.

Какая фигура называется параллелограммом?
Какие признаки параллелограмма мы знаем?
Чем является отрезок KL в треугольнике ADC?
Какие свойства средней линии треугольника нам известны?

4. Парная работа учащихся

№2*. EF – средняя линия трапеции KMNP и треугольника ABC. Докажите, что АС || КР и найдите КР и MN, если EF = 16 см, KP:MN = 3:5. (Ответ: 12 см и 20 см) (Слайд 9)

(Учитель следит за решение задачи, оказывая необходимую помощь слабым учащимся)

Какие свойства средней линии треугольника (трапеции) нам известны?
Какие свойства параллельных прямых нам известны?

№3*. ST – средняя линия треугольника BMC. PQ – средняя линия треугольника AMD. XY – средняя линия трапеции ABCD. Докажите, что PQ || ST и найдите PQ и ST, если XY = 15 см, BC:AD = 1:4. (Ответ: 12 см и 3 см) (Слайд 10)

(Учитель фиксирует пары учащихся, справившихся с задачей, делает замечания по оформлению задачи)

4. Подведение итогов урока.

Учащиеся отвечают на вопросы: (Слайд 11)

Сегодня на уроке я повторил …
Сегодня на уроке я научился …
Мне необходимо еще поработать над …

Учитель выставляет отметки за урок.

5. Домашнее задание.

Пункты 1–8 (повторить теорию). №42, 46. (Слайд 12)

Видео:Средняя линия треугольникаСкачать

Дано: ST – средняя линия

Подведение итогов урока: >>

Дано: ST – средняя линия ?BMC, PQ – средняя линия ?AMD, XY – средняя линия трапеции ABCD. Докажите: PQ||ST. Найдите: PQ и ST. №3*.

Слайд 10 из презентации «Взаимное расположение прямых в пространстве»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Взаимное расположение прямых в пространстве.ppt» можно в zip-архиве размером 58 КБ.

Видео:МАТЕМАТИКА | Средняя линия треугольникаСкачать

Окружность

««Уравнение окружности» 9 класс» — Составить уравнение окружности. Окружность. Составьте уравнение окружности с центром. Центр окружности. Вывод формулы. Цели урока. Координаты точки окружности. Построить по полученным данным окружности в тетради. Работа в группах. Заполните таблицу. Уравнение окружности. Запишите формулу. Найдите координаты центра и радиус.

«Длина окружности 6 класс» — С какой скоростью идет тепловоз? Урок математики в 6 классе Учитель математики: Никонорова Любовь Аркадьевна. Ламберт нашел для ? первые двадцать семь подходящих дробей. Практическая работа. Длина окружности. Но можно найти бесконечную последовательность подходящих дробей. Интересные факты. Диаметр колеса тепловоза равен 180 см.

«Построение касательной к окружности» — Касательная к окружности. Решение. Окружность. Общие точки. Взаимное расположение прямой и окружности. Повторение. Окружность и прямая имеют одну общую точку. Хорда. Окружность и прямая. Диаметр. Теорема об отрезках касательных.

««Окружность» геометрия» — Свойства углов четырехугольника, вписанного в окружность. Прямая, проходящая через середину данного отрезка. Окружность, вписанная в многоугольник. Свойства сторон четырехугольника, описанного около окружности. Касательная к окружности. Радиус является перпендикуляром. Теорема об отрезках пересекающихся хорд.

«Задачи об окружности и круге» — Длина окружности и площадь круга. Чему равна площадь соответствующего данной дуге кругового сектора? Решение задач. 3. Периметр правильного треугольника, вписанного в окружность, равен 6|/3 дм. Найдите площадь закрашенной фигуры.

«Касательная к окружности» — Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Доказательство. Свойство касательной. Отрезки AK и AM называются отрезками касательных, проведенными из A. Свойство + признак: если K – точка окружности, то KM – касательная ? KM ? OK. Построение касательной к окружности через данную на окружности точку K.